丰台区2004年初中毕业统一考试
数 学 试 卷
第I卷(选择题 48分)
一. 选择题(共16个小题,每小题3分,共48分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的。
1. ![]() 的倒数是(
)
的倒数是(
)
A. ![]() B.
B.
![]() C.
5 D.
C.
5 D. ![]()
2. 计算 ![]() 的结果是( )
的结果是( )
A. ![]()
![]() C.
C. ![]() D.
D. ![]()
3. 计算 ![]() 的结果是( )
的结果是( )
A. 1 B.
0 C. ![]() D.
D.
![]()
4. 9的平方根是( )
A. 3 B. ![]() C.
81 D.
C.
81 D. ![]()
5. 我区2004年参加中考的考生预计达到9400人,用科学记数法表示这个数为( )
A. ![]() 人
B.
人
B. ![]() 人 C.
人 C. ![]() 人 D.
人 D. ![]() 人
人
6. 在函数 ![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
7. 如果梯形的中位线的长是6cm,上底长是4cm,那么下底长为( )
A. 2cm B. 4cm C. 6cm D. 8cm
8. 六边形的内角和为( )
 A.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
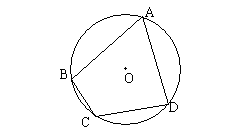
9. 如图,ABCD为圆内接四边形,若 ![]() ,则
,则
![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
10. 如果两圆的半径分别为3和4,圆心距为7,那么这两个圆的位置关系是( )
A. 外切 B. 内切 C. 相交 D. 外离
11. 在 ![]() 中,
中,
![]() ,若
,若
![]() ,则
,则
![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
12. 在直角坐标系中,点
![]() 一定在( )
一定在( )
A. 抛物线 ![]() 上
B. 双曲线
上
B. 双曲线 ![]() 上
上
C. 直线 ![]() 上
D. 直线
上
D. 直线 ![]() 上
上
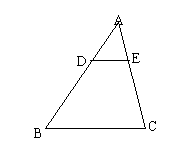 13. 如图,在
13. 如图,在 ![]() 中,
中,
![]() ,若
,若
![]() ,
,
![]() ,则BC的长为( )
,则BC的长为( )
A. 2 B. 4 C. 6 D. 8
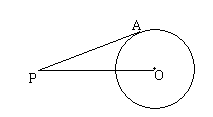 14. 如图,PA切⊙O于点A,若
14. 如图,PA切⊙O于点A,若 ![]() ,则⊙O的半径是( )
,则⊙O的半径是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
15. 若数据 ![]() 的平均数是4,则这组数据的中位数和众数是( )
的平均数是4,则这组数据的中位数和众数是( )
A. 3和2 B. 2和3 C. 2和2 D. 2和4
16. 如果 ![]() ,那么二次函数
,那么二次函数
![]() 的图象大致是( )
的图象大致是( )
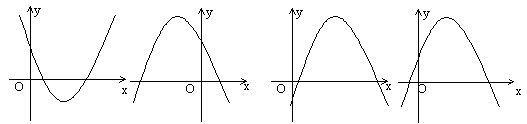
A. B. C. D.
第II卷(非选择题 52分)
二. 填空题(共4个小题,每小题3分,共12分)
17. 计算: ![]()
18. 若 ![]() ,则
,则
![]()
19. 如果圆柱的高为4cm,底面半径为3cm,那么这个圆柱的侧面积是 ![]()
20. 要使一个菱形成为正方形,则需增加的条件是 (填上一个正确的条件即可)。
三. (共2个小题,共9分)
21. (本小题满分4分)
分解因式: ![]()
解:
22. (本小题满分5分)计算: ![]()
四. (本题满分5分)
23. 已知:如图,在平形四边形ABCD中,E、F是对角线AC上的两点,且AE=CF。
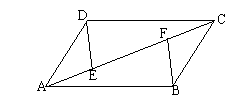 求证:DE=BF
求证:DE=BF
证明:
五. (本题满分6分)
24. 用换元法解方程
![]()
解:
六. (本题满分6分)
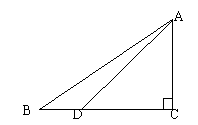 25. 如图,在
25. 如图,在 ![]() 中,
中,
![]() ,
,
![]() ,点D在BC边上,且
,点D在BC边上,且 ![]() ,
,
![]() ,求
,求
![]() 的正切值。
的正切值。
解:
七. (本题满分7分)
26. 甲、乙两名工人接受相同数量的生产任务。开始时,乙比甲每天少做4件,乙比甲多用2天时间,这样甲、乙两人各剩120件;随后,乙改进了生产技术,每天比原来多做6件,而甲每天的工作量不变,结果两人完成全部生产任务所用时间相同。求原来甲、乙两人每天各做多少件?
解:
八. (本题满分7分)
27. 已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点A的坐标为 ![]() ,连结AB,
,连结AB, ![]() ,将
,将
![]() 沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E。
沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E。
(1)求D点坐标;
(2)求经过点A、D的直线的解析式。
解: