杭州市各类高中招生考试数学试题
一、选择题（本题有15个小题，每小题3分，共45分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内。
1. 下列算式是一次式的是
（A）8
（B）
（C）
（D）
2. 如果两条平行直线被第三条直线所截得的8个角中有一个角的度数已知，则
（A）只能求出其余3个角的度数 （B）只能求出其余5个角的度数
（C）只能求出其余6个角的度数 （D）只能求出其余7个角的度数
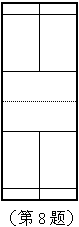
3. 在右图所示的长方体中，和平面A1C1垂直的平面有
（A）4个 （B）3个 （C）2个 （D）1个
4. 蜗牛前进的速度每秒只有1.5毫米，恰好是某人步行速度的1000分之一，那么此人步行的速度大约是每小时
（A）9公里 （B）5.4公里 （C）900米 （D）540米
5. 以下不能构成三角形三边长的数组是
（A）（1，
，2） （B）（，
，
） （C）（3，4，5）
（D）（32，42，52）
6. 有下列说法：①有理数和数轴上的点一一对应；②不带根号的数一定是有理数；③负数没有立方根；④
是17的平方根。其中正确的有
（A）0个 （B）1个 （C）2个 （D）3个
7. 若数轴上表示数x的点在原点的左边，则化简
的结果是
（A）-4x
（B）4x （C）-2x （D）2x
8. 右图为羽毛球单打场地按比例缩小的示意图（由图中粗实线表示），它的宽度为5.18米，那么它的长大约在
（A）12米至13米之间 （B）13米至14米之间
（C）14米至15米之间 （D）15米至16米之间
9. 甲、乙两人分别从两地同时出发，若相向而行，则
小时相遇；若同向而行，则
小时甲追上乙。那么甲的速度是乙的速度的
（A）
倍 （B）
倍 （C）
倍 （D）
倍
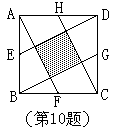
10. 如图，E，F，G，H分别是正方形ABCD各边的中点，要使中间阴影部分小正方形的面积是5，那么大正方形的边长应该是
（A）
（B）
（C）5 （D）
11. 如图，三个半径为的圆两两外切，且ΔABC的每一边都与其中的两个圆相切，那么ΔABC的周长是
（A）12+6 （B）18+6 （C）18+12 （D）12+12
12. 方程
的正根的个数为
（A）0个 （B）1个 （C）2个 （D）3个
13. 要使二次三项式
在整数范围内能进行因式分解，那么整数
的取值可以有
（A）2个 （B）4个 （C）6个 （D）无数个
14. 如图，在RtΔABC中，AF是斜边上的高线，且BD=DC=FC=1，则AC的长为
（A）
（B） （C）
（D）
15. 甲、乙两人连续7年调查某县养鸡业的情况，提供了两方面的信息图（如图）。
甲调查表明：养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只；
乙调查表明：养鸡场的个数由第1年的46个减少到第7年的22个。
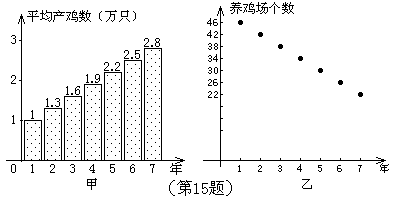
现给出下列四个判断：①该县第2年养鸡场产鸡的数量为1.3万只；②该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量；③该县这7年养鸡场产鸡的数量逐年增长；④这7年中，第5年该县养鸡场出产鸡的数量最多。根据甲、乙两人提供的信息，可知其中正确的判断有
（A）3个 （B）2个 （C）1个 （D）0个
二、填空题（本题有5个小题，每小题4分，共20分）
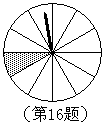
16. 右图是一个被等分成12个扇形的转盘。请在转盘上选出若干个扇形涂上斜线（涂上斜线表示阴影区域，其中有一个扇形已涂），使得自由转动这个转盘，当它停止转动时，指针落在阴影区域的概率为
。
17. 已知一次函数
，当
=3时，
=1，则直线在轴上的截距为__________
18. 如图，过点P引圆的两条割线PAB和PCD，分别交圆于点A，B和C，D，连结AC，BD，则在下列各比例式中，①
；②
；③
，成立的有__________（把你认为成立的比例式的序号都填上）
19. 在关于x1，x2，x3的方程组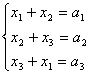
中，已知
，那么将x1，x2，x3从大到小排起来应该是____________
20. 给出一个正方形，请你动手画一画，将它剖分为
个小正方形。那么，通过实验与思考，你认为这样的自然数可以取的所有值应该是_________________
三、解答题（本题有6个小题，共55分）解答应写出文字说明，证明过程或推演步骤
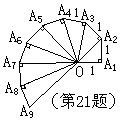21. （本小题满分7分）
在第六册课本的阅读材料中，介绍了一个第七届国际数学教育大会的会徽。它的主题图案是由一连串如图所示的直角三角形演化而成的。设其中的第一个直角三角形OA1A2是等腰三角形，且OA1=A1A2=A2A3=A3A4=……=A8A9=1，请你先把图中其它8条线段的长计算出来，填在下面的表格中，然后再计算这8条线段的长的乘积。
| OA1 | OA2 | OA3 | OA4 | OA5 | OA6 | OA7 | OA8 |
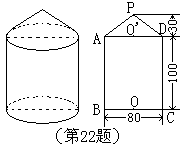22. （本小题满分8分）
要在如图的一个机器零件（尺寸单位：mm）表面涂上防锈漆，请你帮助计算一下这个零件的表面积（参考公式：
，
，
，其中
为底面半径，
为高线，
为母线取3.14，结果保留3个有效数字）。
23. （本小题满分8分）
直线AB交圆于点A，B，点M在圆上，点P在圆外，且点M，P在AB的同侧，∠AMB=50º。设∠APB=
，当点P移动时，求的变化范围，并说明理由。
24. （本小题满分10分）
某航运公司年初用120万元购进一艘运输船，在投入运输后，每一年的总收入为72万元，需要支出的各种费用为40万元。
（1）问：该船运输几年后开始盈利（盈利即指总收入减去购船费及所有支出费用之差为正值）？
（2）若该船运输满15年要报废，报废时旧船卖出可收回20万元，求这15年的年平均盈利额（精确到0.1万元）。
25. （本小题满分10分）
二次函数
的图像的一部分如右图，已知它的顶点M在第二像限，且经过点A（1，0）和点B（0，1）。
（1）请判断实数的取值范围，并说明理由；
（2）设此二次函数的图像与轴的另一个交点为C，当ΔAMC的面积为ΔABC面积的
倍时，求的值。
26. （本小题满分12分）
在ΔABC中，AB=AC，D为BC上一点，由D分别作DE⊥AB于E，DF⊥AC于F；设DE=，DF=，且实数，满足
，并有
；∠A使得方程
有两个相等的实数根
（1）试求实数，的值； （2）试求线段BC的长。