泸州市初中毕业考试暨高中阶段学校招生统一考试
数学试卷
（考试时间：只完成A卷90分钟，完成A、B卷150分钟）
说明：
1．本次考试试卷分为A、B卷，只参加毕业考试的考生只需完成A卷，要参加升学考试的考生必须加试B卷。
2．A卷满分为100分，B卷满分为50分。A、B卷满分为150分。
3．A卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷（1至2页）为选择题，第Ⅱ卷（3至6页）为非选择题；B卷（7至10页）为非选择题。
A卷
第Ⅰ卷 选择题（共60分）
注意事项：
1．第Ⅰ卷共2页，答第Ⅰ卷前，考生务必将自已的姓名、准考证号、考试科目填写在答题卡上，考试结束后，监考人员将试卷和答题卡一并收回。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦擦干净后再选涂其它答案，不能答在试卷上。
一、选择题（共60分，每小题3分）
以下每小题给出的四个选项中，只有一个是符合题目要求的，请选出并把答题卡上对应题目的正确答案标号涂黑。
1．在天气预报图中，零上5度用5℃表示，那么零下5度表示为（ ）
A.5 B.+5℃ C.－5 D.－5℃
2．－3的相反数为（ ）
A.－3 B.3 C.
D.
3．
等于（ ）
A.2 B.－2 C.1 D.－1
4．2003年10月15日，中国“神舟”五号载人飞船成功发射，圆了中国人千年的飞天梦，航天员杨利伟乘飞船在约21小时内环绕地球14圈，其长度约为千米，用科学计数法表示为（ ）
A.5.91×107千米 B. 5.91×108千米 C. 5.91×109千米 D. 5.91×1010千米
5．计算
的结果为（ ）
A.
B.
C.
D.
6．不等式组
的解集是（ ）
A.
B.
C.
D.无解
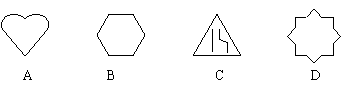7．下列各种图形不是轴对称图形的是（ ）
8．下列各式与
是同类二次根式的是（ ）
A.
B. 
C. 
D. 
9．
分解因式为（ ）
A.
B.
C.
D.
10．函数
中，自变量
的取值范围是（ ）
A.≥1 B.＞1 C.＜1 D.≤1
11．用换元法解方程
，若设
，则原方程可变形为（ ）
A.
B.
C.
D.
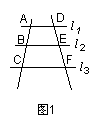
12．已知：如图1，直线
，AB＝4，BC＝6，DE＝3，则EF为（ ）
A.2 B.4.5 C.6 D.8
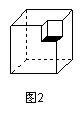
13．如图2，从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为（ ）
A.600 B.599 C.598 D.597
14．抛物线
的开口（ ）
A.向上 B.向下 C.不能确定 D.以上说法都不对
15．函数
的图象大致是（ ）
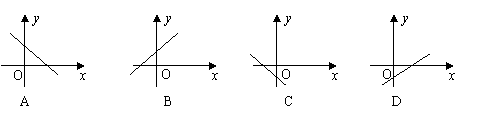
16．一个正多边形的每一个外角都为36°，则它是（ ）
A.正六边形 B.正八边形 C.正九边形 D.正十边形
17．已知：一元二次方程
，当
为何值时方程有两个相等的实数根（ ）
A.
B. 
C. 
D. 
18．两圆的半径分别为8cm和6cm，圆心距为2cm，则两圆的公切线有（ ）
A.1条 B.2条 C.3条 D.4条
19．等腰三角形的两边长分别为2cm、4cm，则周长为（ ）
A. 8cm; B.
10cm; C. 8cm或10cm D.6 cm
20．如图3所示的象棋盘上，若帅位于点（1，－2）上，相位于点（3，－2）上，则炮位于点（ ）
A. （－1，1） B. （－1，2）
C. （－2，1） D. （－2，2）
第Ⅱ卷（非选择题 共40分）
注意事项：
1． 第Ⅱ卷共4页，用钢笔或圆珠笔直接答在试卷上。
2． 答卷前将密封线内的项目填写清楚。
| 题号 | 第Ⅰ卷 | 第Ⅱ卷 | 总分 | 总分人 | 复查人 | ||||
| 二 | 三 | 四 | 合计 | ||||||
| 得分 | |||||||||
二、（本题共15分，每小题5分）
21．计算：
.
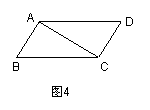
22．如图4，在四边形ABCD中，AD＝CB，∠ACB＝∠CAD. 求证：AB＝CD.
23．解方程
三、（本题共15分，第24题7分，第25题8分）
24．某校在举办“五·四”汇演中，对各班的节目进行打分评比，评比方式是：去掉一个最高分和一个最低分，再算平均分即为最后得分。学校一共请了九名教师当评委，其中初三·一班的得分为：9.34 9.66 9.80 9.23 9.63 9.70 9.81 9.37 9.70.
问：（1）这9个数的中位数是多少？
（2）众数是多少？
（3）该班的最后得分是多少？
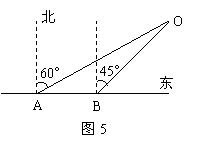
25．如图5，某船由西向东航行，在点A测得小岛O在北偏东60°，船行了10海里后到达点B，这时测得小岛O在北偏东45°。由于以小岛O为圆心16海里为半径的范围内有暗礁，如果该船不改变航向继续航行，有没有触礁的危险？通过计算说明。（供选用数据：
，
）
四、（本题满分10分）
26．如图6，⊙O为△ABC的外接圆，且AB＝AC，过点A的直线⊙O于D，交BC延长线于F，DE是BD的延长线，连结CD.
（1）求证：∠EDF＝∠CDF；
（2）求证：
；
（3）若BD正好是⊙O的直径，且∠EDC＝120°，BC＝6cm，求AF的长.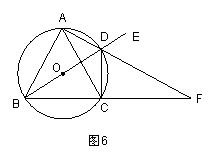
B卷
注意事项：本卷共4页，用钢笔或圆珠笔直接答在试卷上。
| 题号 | 一 | 二 | 三 | 四 | 总分 | 总分人 | 复查人 |
| 得分 |
一、填空题（本题共15分，每小题3分）
1．反比例函数
经过点（1，3），则
＿＿＿.
2．已知：
、
是方程
的两根，则
＝＿＿＿.
3． 牛顿发现“万有引力”定律据说来源于小时候在苹果树下看书，突然一个成熟的苹果掉下来正好落在他的头上，在疼痛这中，他想：为什么苹果往下掉，而不是“飞上天”呢？带着这样的疑问经过长期不断的学习、探索，终于发现了“万有引力”等定律，成为世界上著名的科学家这一。下面图象大致可反应苹果下落过程中速度V随时间t之间的变化情况的是＿＿＿（填数字番号）.
4．
 |
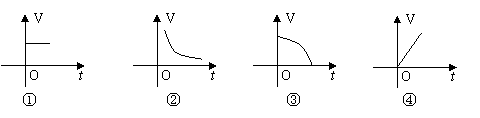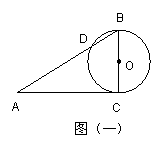
如图（一），在△ABC中，∠C＝90°。以BC为直径作⊙O与斜边AB交于点D，且AD＝3.2cm，BD＝1.8cm，则AC＝＿＿＿cm.
5．把正方体摆放成如图（二）的形状，若从上至下依次为第1层，第2层，第3层，……，则第n层有＿＿＿个正方体.
 |
二、（本题共13分，第6题6分，第7题7分）
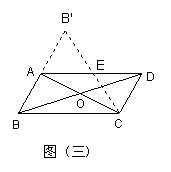
6．如图（三），在
的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转180°，得到
.
（1）求证：以A、C、D、
为顶点的四边形是矩形；
（2）若四边形ABCD的面积S＝12cm2. 求翻转后纸片重叠部分的面积，即
.
7．某企业在“蜀南竹海”收购毛竹进行粗加工，每天可加工8吨，每吨可获利800元；如果对毛竹进行精加工，每天可加工1吨，每吨可获利4000元。由于受条件限制，每天只能采用一种方式加工，要求在一月内（30天）将这批毛竹全部销售。为此企业厂长召集职工开会，让职工讨论如何加工销售更合算？
甲说：将毛竹全部进行粗加工后销售；
乙说：30天都进行精加工，未加工的毛竹直接销售；
丙说：30天中可用几天粗加工，再用几天精加工后销售；
请问厂长应采用哪位说的方案做，获利最大？
三、（本题10分）
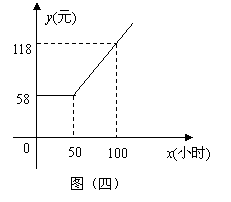
8．某广电局与长江证券公司联合推出广电宽带网业务，用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务，用户交纳上网费的方式有：方式一，每月80元包干；方式二，每月上网时间x（小时）与上网费y（元）的函数关系用图（四）中的折线表示；方式三，以0小时为起点，每小时收费1.6元，月收费不超过120元。若设一用户每月上网x小时，月上网费为y元。
（1）根据图（四），写出方式二中y与x的函数关系式；
（2）试写出方式三中y与x的函数关系式；
（3）若此用户每月上网60小时，选用哪种方式上网，其费用最少？最少费用是多少？
四、（本题12分）
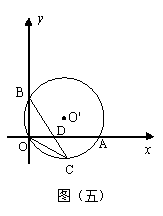
9．如图（五），半径为6.5的⊙
经过原点O，并且与x轴、y轴分别交于A、B两点，线段OA、OB（OA＞OB）的长分别是方程
的两根。
（1）求A、B两点的距离；
（2）求点A和点B的坐标；
（3）已知点C在劣弧OA上，连结BC交OA于D，当
时，求点C的坐标；
（4）若在以点C为顶点，且过点B的抛物线上和在⊙上是否分别存在点P，使△ABD的面积等于△POD的面积，即
？若存在，请求出点P的坐标；如果不存在，请说明理由。注：抛物线
的顶点为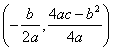
.
