初三数学总复习教案(二)
二元一次方程组
知识结构:
二元一次方程组的解法:代入法消元法、加减消元法。
三元一次方程组的解法:代入法消元法、加减消元法。
重点、热点
消元的思想和方法
目标要求
灵活运用代入法、加减法解二元一次方程组,会解简单的三元一次方程组
【典型例析】
例2(2002年 镇江) 已知二元一次方程组为 则x-y= , x+y=
![]()
![]() x+2y=8
x+2y=8
分析:可以解方程组,求得x、y的值,然后再代入求值,也可以直接利用加减法,求出所求代数式的值
![]() 2x+y=7 ①
2x+y=7 ①
解法一:
x+2y=8 ②
①-②×2 -3y=-9
y=3
把y=3 代入① 得x=2
![]() x=2
x=2
∴原方程组的解为
y=3
![]() x=2
x=2
当 时, x-y=2-3=-1, x+y=2+3=5
y=3
![]() 2x+y=7①
2x+y=7①
解法二:
x+2y=8 ②
①-② ,得 x-y=-1
[①+②]/3 得x+y=5
例2 (2002 云南省) 方程组 的解是 ( ).
的解是 ( ).
A. ![]() B.
B. 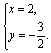 C.
C. ![]() D.
D. ![]()
【特色】考查灵活运用代入法、加减法解二元一次方程组;或者考查我们会对方程的解进行检验.
【解答】
②×2—①, 得 y= —1,
将y= —1代入②,得 ![]() . ∴
. ∴![]()
【拓展】此题可以用代入法求解,也可直接将选支代入进行检验求解.
例3 (2000 重庆) 某工程由甲、乙两队合作6天可完成,厂家需支付甲、乙两队共8700元;乙、丙两队合作10天可完成,厂家需支付乙、丙两队共9500元;甲、丙两队合作5天可完成全部工程的![]() ,厂家需支付5500元.
,厂家需支付5500元.
(1) 甲、乙、丙各队单独完成全部工程各需多少天?
(2)若工期要求不超过15天完成全部工程,问可由那队单独完成此项工程花钱最少?
【特色】本题既考查应用三元方程组解应用题,同时也考查了用整体求值和换元思想.
【解答】(1)设甲、乙、丙单独完成工程分别需x、y、z天,则
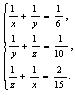 解之,得
解之,得![]()
(2) 设甲队做一天应支付a元,乙队做一天应支付b元,丙队做一天应支付c元. 则有
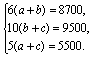 解之,得
解之,得
答:(1)甲、乙、丙各队单独完成全部工程各需10天、15天、30天;(2)由甲队单独完成此项工程花钱最少
【拓展】(1)问中将三个方程相加,整体求出![]() 后,再求出x、y、z较为简单;此法也适合 (2)问中的方程的求解.
后,再求出x、y、z较为简单;此法也适合 (2)问中的方程的求解.
课堂练习:
1.(2001 天津)已知x+y=4,x-y=10,则2xy= .
2.(2000天津)已知![]() 则
则![]() = .
= .
3.(2001 重庆)若![]() 则m+n的值为(
).
则m+n的值为(
).
A. 1 B. 2 C. 3 D. -3
4.(2002 黄冈)不论m为何实数,直线y=x+2m与直线y=-x+4的交点不可能在( ).
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.(2002 大连)当抛物线的解析式中含有字母系数时,随着系数中字母的取值的不同,抛物线的顶点坐标也发生变化.
例如:有抛物线![]() ①
①
有![]() ……②
……②
抛物线的顶点坐标为(m , 2 m – 1).即![]()
当m的值变化时,x、y的值也随之变化,因此y值也随x的变化而变化 .
将③代入④,得 y = 2 x – 1.
可见,不论m取何实数时,抛物线顶点的纵坐标y和横坐标x都满足关系式:y = 2 x – 1.
解答问题:
(1)在上述过程中,由①得到②所用的数学方法是 , 其中运用了 公式 .
由③、④得到⑤所用的数学方法是 ;
(2)根据阅读材料提供的方法,确定抛物线![]() 顶点的纵坐标y与横坐标x之间的关系式
顶点的纵坐标y与横坐标x之间的关系式