初 三 数 学（第1讲）
苏州立达中学 2004-2005学年度第 一 学 期 期初考试试卷
班级___________学号______姓名______________
一、选择题：
( )1、下列式子中，不是同类二次根式的组是
A、
； B、
； C、
； D、
( )2、在实数3.1416，
，0.417，－2π，
，
，(－0.3)2，
，
－0.…， 中无理数有x个，整数有y个，非负数有z个，则x＋y＋z＝
A、14； B、13； C、15； D、12
( )3、已知点P的坐标为(1＋ ，－2－a)，则点P在
A、第一象限； B、第二象限； C、第三象限； D、第四象限。
( )4、在△ABC和△A/B/C/中，已知AB＝9cm，BC＝8cm，CA＝5cm，A/B/＝3cm，
B/C/＝ cm，C/A/＝ cm，那么
A、∠A＝∠A/； B、∠A＝∠C/； C、∠A＝∠B/； D、∠C＝∠B/
( )5、若点P(a，b)关于x轴的对称点P/ 在第三象限，那么直线y＝ax＋b的图象不经过
A、第一象限； B、第二象限； C、第三象限； D、第四象限
( )6、如图，正方形ABCD的对角线AC、BD相交于点O，E是BC
的中点，DE交AC于F，若DE＝12，则EF＝
A、8； B、6； C、4； D、3
( )7、如图，矩形ABCD，CEBD于E，EFAB于F，若AB＝2，
BC＝1，则EF等于
A、
；
B、
； C、
； D、
( )8、如图，在同一平面直角坐标系中，正比例函数y＝(m－1)x与反比例函数y＝ 的图
象的大体位置不可能是
( )9、已知cosα＝
，则
的值是
A、
； B、 ； C、 ；
D、0
( )10、某中学数学教研组有30名教师，将他们的年龄分成3组，在32～42岁组内有18名
教师，那么这个小组的频率为
A、0.1； B、0.5； C、0.6； D、0.8
二、填空题：
11、
的平方根是______________。
12、已知点A(－4，a)，B(－2，b)都在直线y＝ x＋k(k为常数)上，则a与b的大小关系是
_____________ (填“＜”、“＝”或“＞”)
13、一个多边形面积扩大到原来的2倍，且与原多边形相似，则其周
长是原来的______________。
14、如图，四边形AOCB是平行四边形，AO＝3，AB＝2，∠C＝600，
则点B坐标是___________。
15、从形状和大小都相同的9张数字卡(1～9)中任意抽1张，抽出的恰是①奇数，②不小于
6的数，③不大于2的数，④大于9的数。将这些事件发生的机会从小到大在直线上的
排序是___________________。
16、已知锐角α满足cosα＝
，则m的取值范围是__________。
17、如图，在矩形ABCD中，AB＝2，BC＝3，P是BC边上与
B、C两点不重合的任意一点，设PA＝x，D点到PA的距离
为y，则y与x之间的函数关系式是_________________。
18、如图，小正方形的边长是1，把图形剪开后重新拼成一个面积为10的大正方形，请你在
原图上用虚线画出剪开线，并在第二个图上画出拼好的这个正方形。
 |
三、解答题：
19、计算：
20、计算：
21、如图，某同学测量校园内的一棵树AB的高度，现已用仪器测得了仪器到树的距离DB和仪器的高CD的三组数据，并由数据情况制成了如下的条形统计图和仰角情况的折线统计图。
 | |||
 | |||
请你利用两个统计图提供的信息完成以下任务：
(1)把统计图中的相关数据填入相应的表中；
(2)根据测得的样本平均数计算出树高AB(精确到0.1m)
| 仪器与树之间距离BD长 | 19.97 | ||
| 测量仪器的高CD | 1.21 | ||
| 仰角α的度数 | 29040/ |
22、已知△ABC的面积为S。
(1)如图(a)，将AB三等分，D1、D2是三等分点，且D1E1∥D2E2∥BC，求梯形D1E1E2D2
的面积(用S表示)；
(2)如图(b)，将AB五等分，D1、D2、D3、D4是五等到分点，且D1E1∥D2E2∥D3E3∥D4E4
∥BC，那么梯形D2E2E3D3的面积是多少(用S表示)？
(3)如图(c)，将AB (2n－1)等分(n为大于3的一个自然数)，类似(2)得到梯形Dn－1En－1EnDn
(阴影部分)，那么这个梯形的面积是多少(用S表示)？
23、已知：Rt△AOB中，∠AOB＝900，OA＝3厘米，OB＝4厘米。以O为坐标原点建立
如图所示的平面直角坐标系。设P、Q分别为AB边，OB边上的动点，它们同时分别
从点A、O向B点匀速移动，移动的速度都为1厘米 / 秒。设P、Q移动时间为t秒(0
≤t≤4)。
⑴过点P作PM⊥OA于M。求出点P的坐标(用t表示)；
⑵求△OPQ的面积S(厘米 2)与移动时间t(秒)之间的函数关系式；
*⑶①说明无论t为何值，△OPQ不可能为正三角形；②若点P的移动速度不变，试改
变点Q的运动速度，使△OPQ为正三角形，求出点Q的运动速度和此时的t值。
 |
期初试卷答案
一、1、D 2、A 3、D 4、C 5、C 6、C 7、A 8、D 9、D 10、C
二、11、
12、
13、
倍 14、
15、④③②① 16、
17、
18、
三、19、原式
20、原式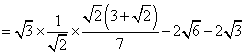
。
21、⑴
| 仪器与树之间距离BD长 | 19.97 | 19.70 | 20.51 |
| 测量仪器的高CD | 1.21 | 1.23 | 1.22 |
| 仰角 |
|
|
|
的度数
⑵解：
，
，
，
，
。
22、⑴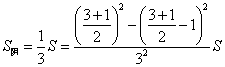
。
⑵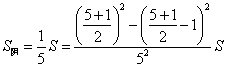
⑶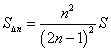
，
，
。
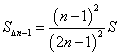23、⑴
，作
，
，则
，
，
，
，
，
。
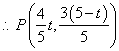⑵
。
⑶①若三角形是等边三角形，则应有
，而
，则
，
（一切
值）。 ②
，
，
，
，
。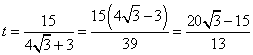