2004年福建省泉州市初中毕业、升学考试测试卷
数学试题
(满分:150分;考试时间:120分钟)
一、填空题(每小题3分,共36分)
1、计算:![]() ;
;
2、某公司一名员工,月工资由1200元增加了10%后达到 元;
3、若![]() ,
,![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() ;
;
4、梯形的上底长为4,中位线长为6,则下底长为 ;
5、如图,⊙O为△ABC的外接圆,若![]() ,则
,则![]() 度;
度;
 |
6、函数![]() 中自变量
中自变量![]() 的取值范围为
;
的取值范围为
;
7、点![]() 关于
关于![]() 轴对称的点的坐标为
;
轴对称的点的坐标为
;
8、两圆的半径分别为3、2,它们的圆心距是1,则这两圆的位置关系是 ;
9、人数相等的甲、乙两班学生参加同一次数学测验,班级平均分与方差分别为:![]() 甲
甲![]() ,
,![]() 乙
乙![]() ,
,![]() 甲
甲![]() ,
,![]()
![]() 甲
甲![]() ,则测验成绩较整齐的是
班;
,则测验成绩较整齐的是
班;
10、圆锥的底面半径是4,母线长为5,则圆锥的侧面积等于 ;
11、用正三角形与正方形作平面镶嵌,则在它的每一个顶点周围有3个正三角形和 个正方形;
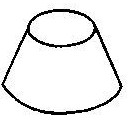 12、一个圆台形物体的上底面积是下底面积的
12、一个圆台形物体的上底面积是下底面积的![]() ,如果如图放在桌上,对桌面的压强是200帕,翻过来放,对桌面的压强应是
帕(压强P、压力F与受力面积S之间的关系式为
,如果如图放在桌上,对桌面的压强是200帕,翻过来放,对桌面的压强应是
帕(压强P、压力F与受力面积S之间的关系式为![]() );
);
二、选择题(每小题4分,共24分)
每小题有四个答案,其中有且只有一个答案是正确的,请把正确答案的代号,写在题后的括号内,答对的得4分,答错、不答或答案超过一个的一律得0分。
13、气温是零下4摄氏度,应记作( )
A、![]() ; B、 4; C、
; B、 4; C、 ![]() ; D、
; D、![]()
14、计算![]() 的结果应是( )
的结果应是( )
A、![]() ;
B、
;
B、![]() ; C、
; C、![]() ; D、
; D、![]() ;
;
15、不等式组![]() 的解集是( )
的解集是( )
A、![]() ; B、
; B、![]() ; C、
; C、 ![]() ; D、
; D、![]() ;
;
16、如果一个角的补角是![]() ,那么这个角的余角为( )
,那么这个角的余角为( )
A、![]() ; B、
; B、![]() ; C、
; C、![]() ; D、
; D、![]() ;
;
17、过点![]() 的正比例函数解析式是( )
的正比例函数解析式是( )
A、![]() ; B、
; B、![]() ; C、
; C、![]() ; D、
; D、![]() ;
;
18、先作半径为![]() 的第1个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,……,则按以上规律作出的第8个圆的外切正六边形的边长为( )
的第1个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,……,则按以上规律作出的第8个圆的外切正六边形的边长为( )
A、 ![]() ; B、
; B、 ![]() ; C、
; C、![]() ; D、
; D、![]() ;
;
三、解答题(共90分)
19、(8分)计算:
![]() ;
;
解:
20、(8分)先化简下面的代数式,再求值:
![]() ,其中
,其中![]() ,
,![]() ;
;
解:
21、(8分)用换元法解方程:
![]() ;
;
解;
22、(8分)如图,已知点A、C、B、D在同一直线上,![]() ,
,![]() ,
,![]() 。
。
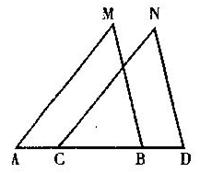 求证:
求证:![]() 。
。
证明:
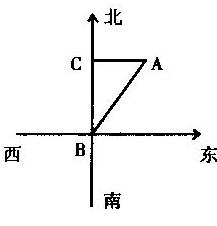 23、(8分)如图,一艘船向北航行,上午8时到达B处,看到一灯塔在它的北偏东
23、(8分)如图,一艘船向北航行,上午8时到达B处,看到一灯塔在它的北偏东![]() 距离为72海里的A处,上午10时到达C处,看到灯塔A在它的正东方向,试求这艘船航行的速度(精确到
距离为72海里的A处,上午10时到达C处,看到灯塔A在它的正东方向,试求这艘船航行的速度(精确到![]() 海里/时,供选用的数据:
海里/时,供选用的数据:![]() ,
,![]() ,
,![]() ,
,![]() );
);
解:
24、(8分)为了了解中学生的身体发育情况,对某中学同年龄的一些女学生的身高进行测量,现将测量到的部分数据列在下表(表中分组数据的单位是厘米):
| 分组 |
|
|
|
|
| 合计 |
| 频数 | 4 | 16 | 4 | |||
| 频率 |
|
|
|
|
|
(1)将上表中所缺的数据补充完整(直接填在表中);
(2)从(1)中所填完整的频率分布表中你能得到哪些结论?请写出其中两条结论与他人交流;
25、(8分)如图,△ABF、△ADF均内接于⊙O,AB是⊙O的直径,AD平分![]() ,直线
,直线![]() 与⊙O相切于D且与AF的延长线相交于点E。
与⊙O相切于D且与AF的延长线相交于点E。
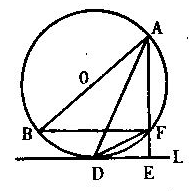 (1)求证:BF∥DE;
(1)求证:BF∥DE;
(2)若![]() ,
,![]() ,试求AD的长;
,试求AD的长;
26、(8分)已知抛物线![]() 。
。
(1)求这条抛物线的对称轴;
(2)设⊙A的半径为2,圆心A的坐标是![]() ,若⊙B与⊙A关于原点O中心对称,请问⊙B与这条抛物线的对称轴有怎样的位置关系?为什么?
,若⊙B与⊙A关于原点O中心对称,请问⊙B与这条抛物线的对称轴有怎样的位置关系?为什么?
解:
 |
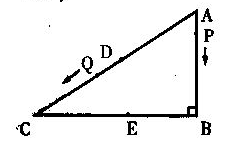
27、(13分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 厘米,质点P从A点出发沿线路
厘米,质点P从A点出发沿线路![]() 作匀速运动,质点Q从AC的中点D同时出发沿线路
作匀速运动,质点Q从AC的中点D同时出发沿线路![]() 作匀速运动逐步靠近质点P,设两质点P、Q的速度分别为1厘米/秒、
作匀速运动逐步靠近质点P,设两质点P、Q的速度分别为1厘米/秒、![]() 厘米/秒(
厘米/秒(![]() ),它们在
),它们在![]() 秒后于BC边上的某一点E相遇。
秒后于BC边上的某一点E相遇。
(1)求出AC与BC的长度;
(2)试问两质点相遇时所在的E点会是BC的中点吗?为什么?
(3)若以D、E、C为顶点的三角形与△ABC相似,试分别求出![]() 与
与![]() 的值;
的值;
 |
28、(13分)某市为更有效地利用水资源,制定了用水标准:如果一户三口之家每月用水不超过标准用水量,按每立方米![]() 元收费;如果超过标准用水量,超过部分按每立方米
元收费;如果超过标准用水量,超过部分按每立方米![]() 元收费,其余仍按每立方米
元收费,其余仍按每立方米![]() 元收费。小红一家三人,1月份共用水11立方米,支付水费
元收费。小红一家三人,1月份共用水11立方米,支付水费![]() 元。
元。
(1)问小红一家1月份用水是否超过标准用水量,为什么?
(2)设某户三口之家用水量为![]() 立方米,应交水费
立方米,应交水费![]() 元,当此户用水量超标时,请求出
元,当此户用水量超标时,请求出![]()
![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)某单位共有20户三口之家,某月共交水费![]() 元,若其中超标的用户平均每户用水12立方米,求这个月该单位用水量未超标的用户最多能有多少户?
元,若其中超标的用户平均每户用水12立方米,求这个月该单位用水量未超标的用户最多能有多少户?