2004年河北省初中生统一考试
数学试卷
本试卷分卷Ⅰ和卷Ⅱ两部分；卷Ⅰ为选择题，卷Ⅱ为非选择题.
本试卷满分为120分，考试时间为120分钟.
卷Ⅰ（选择题，共20分）
注意事项：1. 答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上，考试结束，监考人员将试卷和答题卡一并收回.
2. 每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.
一、选择题（本大题共10个小题；每小题2分，共20分.在每小题给出的四个选项中，只
有一项是符合题目要求的）
1. 2的倒数是
A．
B．
C．
D．
2. 第五次全国人口普查结果显示，我国的总人口已达到人，用科学记数法表
示这个数，正确的是
A．1.3×108 B．1.3×109 C．0.13×1010 D．13×109
3. 化简
，结果正确的是
A．
B．
C．
D．
4. 若x1，x2是一元二次方程2x2-3x+1=0的两个根，则
的值是
A．
B．
C．
D．
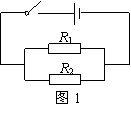5. 图1所示的电路的总电阻为10Ω，若R1=2R2，则R1，R2的值分别是
A．R1=30Ω，R2=15Ω B．R1=
Ω，R2=
Ω
C．R1=15Ω，R2=30Ω D．R1=Ω，R2=Ω
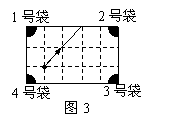6. 图2是一个经过改造的台球桌面的示意图，图中四个角上的阴影
部分分别表示四个入球孔.如果一个球按图中所示的方向被击出
（球可以经过多次反射），那么该球最后将落入的球袋是
A．1 号袋 B．2 号袋
C．3 号袋 D．4 号袋
7. 如图3—1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围
成图3—2所示的一个圆锥模型.设圆的半径为r，扇形半径为
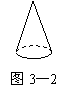R，则圆的半径与扇形半径之间的关系为
A．R=2r
B．R=r
C．R=3r D．R=4r
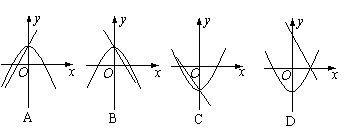
8. 在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为
 |
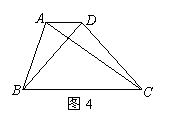9. 如图4，在梯形ABCD中，AD//BC，对角线AC⊥BD，且AC=12，BD=9，则此梯形的
中位线长是
A．
B．
C．
D．
10. 小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的
布料生产一批形状如图5所示的风筝，点E，F，G，H分别
是四边形ABCD各边的中点.其中阴影部分用甲布料，其余
部分用乙布料（裁剪两种布料时，均不计余料）.若生产这批
风筝需要甲布料30匹，那么需要乙布料
A．15匹 B．20匹
C．30匹 D．60匹
2004年河北省初中生升学统一考试
数学试卷
卷Ⅱ（非选择题，共100分）
注意事项：1. 答卷Ⅱ前，将密封线左侧的项目填写清楚.
2. 答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
二、填空题（本大题共10个小题；每小题2分，共20分.把答案写在横线上）
11. --8的值是 .
12.
已知
，则
的余角等于
.
13.
不等式组
的解集是
.
14. 分解因式：x2+2xy+y2-4= .
15. 若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式，则y= .
16. 用换元法解分式方程
时，如果设
，那么原方程可化为关于y的一元二次方程的一般形式是
.
17. 如图6，若将四根木条钉成的矩形木框变形为平行四边形ABCD
的形状，并使其面积为矩形面积的一半，则这个平行四边形的
一个最小内角的值等于 .
18. 若反比例函数
的图象过点（3，-4），则此函数的解析式为
.
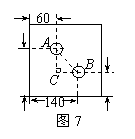
19. 图7是一个外轮廓为矩形的机器零件平面示意图，根据图中标出
尺寸（单位：mm）计算两圆孔中心A和B的距离为 .
20. 扑克牌游戏
小明背对小亮，让小亮按下列四个步骤操作：
第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；
第二步 从左边一堆拿出两张，放入中间一堆；
第三步 从右边一堆拿出一张，放入中间一堆；
第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.
这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .
三、解答题（本大题共8个小题；共80分.解答应写出文字说明、证明过程或演算步骤）
21. （本小题满分8分）
已知
，求
的值.
22. （本小题满分8分）
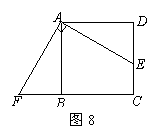已知：如图8，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF.
求证：DE=BF.
23. （本小题满分8分）
为了普及环保知识，增强环保意识，某中学组织了环保知识竞赛活动.
初中三个年级根据初赛成绩分别选出了10名同学参加决赛，这些选手的决赛成绩（满分为100分）如下表所示：
| 决赛成绩（单位：分） | |
| 初一年级 | 80 86 88 80 88 99 80 74 91 89 |
| 初二年级 | 85 85 87 97 85 76 88 77 87 88 |
| 初三年级 | 82 80 78 78 81 96 97 88 89 86 |
（1）请你填写下表：
| 平均数 | 众数 | 中位数 | |
| 初一年级 | 85.5 | 87 | |
| 初二年级 | 85.5 | 85 | |
| 初三年级 | 84 |
（2）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
① 从平均数和众数相结合看（分析哪个年级成绩好些）；
② 从平均数和中位数相结合看（分析哪个年级成绩好些）.
（3）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些？并说明理由.
24. （本小题满分8分）
如图9—1，一个圆球放置在V形架中.图9—2是它的平面示意图，CA和CB都是⊙O
的切线，切点分别是A，B.如果⊙O的半径为
cm，且AB=6cm，求∠ACB.
 |
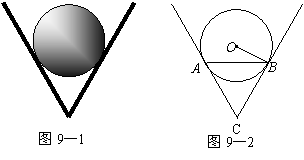25. （本小题满分12分）
如图10—1是某段河床横断面的示意图.查阅该
河段的水文资料，得到下表中的数据：
| x(米) | 5 | 10 | 20 | 30 | 40 | 50 |
| y(米) | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
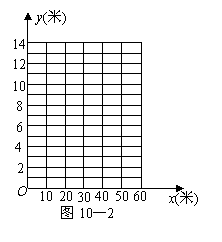（1）请你以上表中的各对数据（x，y）作为点的坐标，
尝试在图10—2所示的坐标系中画出y关于x的
函数图象；
（2）①填写下表：
| x | 5 | 10 | 20 | 30 | 40 | 50 |
|
|
②根据所填表中数据呈现的规律，猜想出用x表示y
的二次函数的表达式： .
（3）当水面宽度为36米时，一艘吃水深度（船底部到水面的距离）为1.8米的货船能
否在这个河段安全通过？为什么？
26. （本小题满分12分）
我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图11—1）.
探索下列问题：
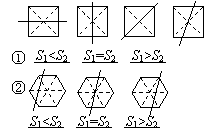
（1）在图11—2给出的四个正方形中，各画出一
条直线（依次是：水平方向的直线、竖直方
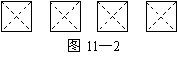向的直线、与水平方向成45°角的直线和
任意的直线），将每个正方形都分割成面积
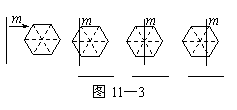相等的两部分；
（2）一条竖直方向的直线m以及任意的直线n，
在由左向右平移的过程中，将正六边形分成
左右两部分，其面积分别记为S1和S2.
①请你在图11—3中相应图形下方的横线上
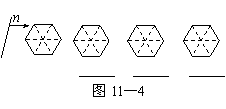分别填写S1与S2的数量关系式（用“<”，
“=”，“>”连接）；
②请你在图11—4中分别画出反映S1与S2
三种大小关系的直线n，并在相应图形下
方的横线上分别填写S1与S2的数量关系
式（用“<”，“=”，“>”连接）.
（3）是否存在一条直线，将一个任意的平面图形（如图11—5）分割成面积相等的两部分?请简略说出理由.
27. （本小题满分12分）
光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台.现将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表：
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地区 | 1800元 | 1600元 |
| B地区 | 1600元 | 1200元 |
（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y(元)，求y与x间的函数关系式，并写出x的取值范围；
（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说
明有多少种分派方案，并将各种方案设计出来；
（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提
出一条合理建议.
28. （本小题满分12分）
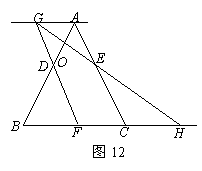已知：如图12，等边三角形ABC的边长为6，点D，E分别在边AB，AC上，且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动，设点F运动的时间为t秒.当t>0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O.
（1）设△EGA的面积为S，写出S与t的函数关系式；
（2）当t为何值时，AB⊥GH；
（3）请你证明△GFH的面积为定值；
（4）当t为何值时，点F和点C是线段BH的三等分点.
2004年河北省初中生升学统一考试
数学试题参考答案及评分标准
说明：
1. 各地阅卷过程中,如考生还有其它正确解法,可参照评分标准步骤酌情给分.
2. 坚持每题评阅到底的原则，当考生的解答在某一步出现错误,影响了后继部分时，如果该
步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不
超过后继部分给分数的一半；如果这一步后面的解答有较严重的错误,就不给分.
3. 解答右端所注分数,表示正确做到这一步应得的累加分数.
4. 只给整数分数.
一、选择题（每小题2分，共10分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | D | A | A | B | D | B | C | C |
二、填空题（每小题2分，共20分）
11. -8；12. 22°；13. 2<x<3； 14. (x+y+2) (x+y-2)；15. (x-1)2+2；16. y2-3y+2=0； 17. 30°；18.
；19. 100mm；20. 5.
三、解答题（本大题8个小题，共80分）
21. （本小题共8分）
解：
……………………………3分
……………………………………………6分
当时，原式
…………………………………………8分
22. （本大题共8分）
证明：∵四边形ABCD是正方形，∴AB=AD，∠BAD=∠ADE=∠ABF=90°.…………2分
∵EA⊥AF，∴∠BAF+∠BAE=∠BAE+∠DAE=90°，∴∠BAF=∠DAE， ……5分
∴Rt△ABF≌Rt△ADE，∴DE=BF. ………………………………………………8分
23. （本小题共8分）
解：（1）
| 年级 | 平均数 | 众数 | 中位数 |
| 初一年级 | 85.5 | 80 | 87 |
| 初二年级 | 85.5 | 85 | 86 |
| 初三年级 | 85.5 | 78 | 84 |
（每空1分）………4分
（2）①∵平均数都相同，初二年级的众数最高，∴初二年级的成绩好一些； ………5分
②∵平均数都相同，初一年级的中位数最高，∴初一年级的成绩好一些.………6分
24. （本大题共8分）
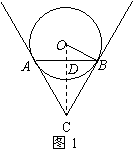解：如图1，连结OC交AB于点D。 ………………1分
∵CA，CB分别是⊙O的切线，
∴CA=CB，OC平分∠ACB，∴OC⊥AB。 ………4分
∵AB=6，∴BD=3。在Rt△OBD中，
……6分
∵B是切点，∴OB⊥BC，∴∠OCB=30°，
∴∠ACB=60°. ……………………………………8分
25. （本小题共12分）
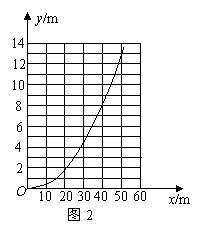
解：（1）图象如图2所示. ……………………………………………………2分
 |
（2）① 填表正确； …………………………………………………………5分
| x | 5 | 10 | 20 | 30 | 40 | 50 |
|
| 200 | 200 | 200 | 200 | 200 | 200 |
② 
………………………………………………………8分
（3）当水面宽度为36米时，相应的x为18，此时水面中心的
……………………………………10分
因为货船吃水深度为1.8m，显然，1.62<1.8,所以当水面宽度为36米时，该货船不能通过这个河段. ………………………12分
26. （本小题共12分）
（1） ………………………………2分
（2） ………………………………………………5分
…………………………………………8分
（3）存在. …………………………………………10分
对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中，当图形被直线l分割后，设直线l两侧图形的面积分别为S1，S2.两侧图形的面积由S1<S2（或S1>S2）的情形，逐渐变为S1>S2（或S1<S2）的情形，在这个平移过程中，一定会存在S1=S2的时刻.因此，一定存在一条直线，将一个任意平面图形分割成面积相等的两部分. ………………………………………………………………12分
27. （本小题共12分）
解：（1）若派往A地区的乙型收割机为x台，则派往A地区的甲型收割机为(30-x)台；派往B地区的乙型收割机为（30-x）台，派往B地区的甲型收割机为（x-10）台. …………………………………………………………………………2分
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000.
x的取值范围是：10≤x≤30(x是正整数).……………………………………5分
（2）由题意得200x+74000≥79600,
解不等式得x≥28.由于10≤x≤30，∴x取28，29，30这三个值，
∴有3种不同分配方案. ……………………………………………………7分
① 当x=28时，即派往A地区甲型收割机2台，乙型收割机28台；派往B
地区甲型收割机18台，乙型收割机2台.
② 当x=29时，即派往A地区甲型收割机1台，乙型收割机29台；派往B
地区甲型收割机19台，乙型收割机1台.
③ 当x=30时，即30台乙型收割机全部派往A地区；20台甲型收割机全部派往B地区. ……………………………………………………………10分
（3）由于一次函数y=200x+74000的值y是随着x的增大而增大的，所以，当x=30时，y取得最大值.如果要使农机租赁公司这50台联合收割机每天获得租金最高，只需x=30，此时，y=6000+74000=80000.
建议农机租赁公司将30台乙型收割机全部派往A地区；20台甲型收割要全部派往B地区，可使公司获得的租金最高.…………………………………12分
28.（ 本小题共12分）
解：（1）如图3，
又∵AB=6，AD=2，∴DB=4，由于BF=t，
……………………………………1分
过点E作EK⊥AG，垂足为K.
∵∠BCA=60°，∴∠CAK=60°，
∴∠AEK=30°，
∵AE=2，∴AK=1，
………………………2分（2）如图3，连结DE，由AD=AE可知，△ADE为等边三角形.
若AB⊥HE，则AO=OD，∠AEO∵GA//DE，∴∠AGE=∠GED，∴∠AGE=∠AEG，∴AG=AE=2.
………………………………4分
∴t=4.即当t=4时，AB⊥GH. ………………5分
（3）法一：
，由合比性质得
………………7分
∵△ABC与△GFH的高相等，∴S△GFH= S△ABC=
∴不论t为何值，△GFH的面积均为
. ………………………………8分
法二：∵△GAD∽△FBD，
∵△GAE∽△HCE，
…………………………6分
当点F与点C重合时，BC=FH，
当点F在BC边上时，BC=BF+FC=CH+FC=FH，
当点F在BC的延长线上时，BC=BF-FC=CH-FC=FH，
∴BC=FH.
∴S△GFH= S△ABC=
∴不论t为何值，△GFH的面积均为. ………………………………8分
（4）∵BC=FH，∴BF=CH.
①当点F在线段BC边上时，若点F和点C是线段BH的三等分点，则BF=FC=CH， ∵BC=6，∴BF=FC=3，
∴当t=3时，点F和点C是线段BH的三等分点. ……………………………10分
② 如图4，点F在BC的延长线上时，
若点F和点C是BH的三等分点，
则BC=CF=FH.
∵BC=6，
∴CF=6，
∴BF=12.
∴当t=12时，点F和点C是线段BH的三等分点. …………………………12分
（说明：本题解法较多，对于其它正确解法，请参照评分标准按步骤给分）