哈尔滨市2004年初中升学考试数学试卷
第I卷 选择题(30分)(涂卡)
一、单项选择题(每小题3分,共30分)
1.下列各式正确的是()
(A) (-a)2 = a2 (B) (-a)3 = a3 (C) -a2 = -a2 (D) -a3 = a3
2.以下列各组线段长为边,能组成三角形的是()
(A) 1cm,2cm,4cm (B) 8cm,6cm,4cm (C) 12cm,5cm,6cm (D) 2cm,3cm,6cm
![]() 3.不等式组 的整数是()
3.不等式组 的整数是()
(A) -1,0,1 (B) -1,1 (C) -1,0 (D) 0,1
4.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在()
(A) 第一象限 (B)第二象限 (C)第三象限 (D) 第四象限
5.下列图形中,既是轴对称图形又是中心对称图形的是()
(A)等边三角形 (B)等腰梯形 (C)平行四边形 (D) 正六边形
6.下列命题中,正确命题的个数是()
①一个锐角的余角还是一个锐角;②垂直于半径的直线是圆的切线;
③一个数的算术平方根一定比这个数小;④平分弦的直径垂直于这条弦.
(A)0 (B) 1 (C) 2 (D) 3
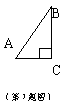 7.如图,已知:Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线BC为轴旋转一周得一个圆锥,则这个圆锥的表面积为()cm2 .
7.如图,已知:Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线BC为轴旋转一周得一个圆锥,则这个圆锥的表面积为()cm2 .
(A)65π (B) 90π (C) 156π (D) 300π
![]() 8.若 2 = -a,则实数a在数轴上的对应点一定在()
8.若 2 = -a,则实数a在数轴上的对应点一定在()
(A)原点左侧 (B)原点右侧
(C)原点或原点左侧 (D)原点或原点右侧
9. ⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么认P为圆心,且与⊙O相切的圆的半径一定是()
(A)1或5 (B)1 (C)5 (D)1或4
10.直线y=x-1与坐标轴交于A、B两点,点C在坐标轴上,△ABC为等腰三角形,则满足条件的点C最多有()个
(A)4 (B)5 (C)7 (D)8
第II卷 非选择题(90分)
二、填空题(每小题3分,共30分)
11.2003年我国国内生产总值(GDP)为116694亿元,用四舍五入法保留三个有效数字,用科学记数法表示约为 亿元.
 | |||
![]()
![]()
![]()
![]() 12.若 = ,则 = .
12.若 = ,则 = .
|
![]()
![]() 14.函数y= + 中自变量x的取值范围是 .
14.函数y= + 中自变量x的取值范围是 .
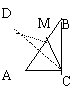
15.如图,在RtΔABC,∠ACB=900, ∠A<∠B,CM是斜边AB的中线,将ΔACM沿直线
CM折叠,点A落在点C处,如果CD恰好与AB垂直,那么∠A等于 度.
16.如图,已知:AB和CD为⊙O的两条直径,弦CE//AB,![]() 的度数为400,则
的度数为400,则
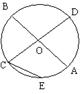 ∠BOC=
度.
∠BOC=
度.
17.观察下列等式9-1=8
16-4=12
25-9=16
|
…………
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n的等式表示这个规律为
.
18.反比例函数y=![]() (k是常数,k≠0)的图像经过点(a,-a),那么k 0(填“>”或“<”).
(k是常数,k≠0)的图像经过点(a,-a),那么k 0(填“>”或“<”).
19.一个多边形的每一个外角都等于360,则该多边形的内角和等于 度.
![]()
![]() 20.若⊙O的直径AB为2,弦AC为 ,弦AD为 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为
.
20.若⊙O的直径AB为2,弦AC为 ,弦AD为 ,则S扇形OCD(其中,2S扇形OCD<S⊙O)为
.
三、解答题(其中21题4分,22题5分,23题4分,24—25题各5分,26—28题各6分,29题9分,30题10分,共60分)
21.(本题4分)
 先化简 ÷(x-2+ )再求值,其中x=tan450-cos300.
先化简 ÷(x-2+ )再求值,其中x=tan450-cos300.
| C |
22.(本题5分)
用换元法解方程:x2+2x-2= .
23.(本题4分)
|
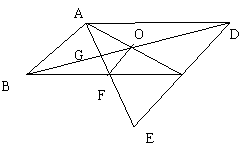
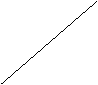
如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,
连结AE,分别交BC、BD于点F、G,连结AC交BD于O,连结OF.
求证:AB=2OF.
24.(本题5分)
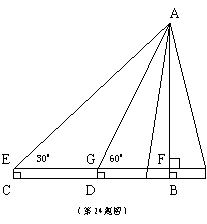
如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是300和600.已知测角仪器高CE=1.5米,CD=30米.
求塔高AB.(答案保留根号)
25.(本题5分)
中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市4万名初中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如下图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是30.
(1)本次调查共抽测了多少名学生?
(2)本次调查抽测的数据的中位数应在哪个小组?说明理由.
(3)如果视力在4.9—5.1(含4.9、5.1)均属正常,那么全市初中生视力正常的约有多少人?
 | |||
 | |||
26.(本题6分)
如图:⊙O1与⊙O2外切于点P,O1O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C,BE是⊙O1的直径,过点B作BF┴O1P,垂足为F,延长BF交PE于点G.
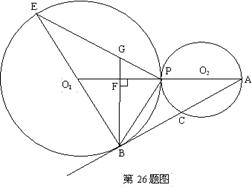 (1)求证:PB2=PG·PE;
(1)求证:PB2=PG·PE;
(2)若PF=![]() ,tan∠A=
,tan∠A=![]() ,求:O1O2的长.
,求:O1O2的长.
27.(本题6分)
“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,以满足市场需求,已知该厂家生产三种不同型号的手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.
(1)若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完.请你帮助商场计算一下如何购买.
(2)若商场同时购进三种不同型号的手机共40部,并将60000元恰好用完,并且要求乙种型号手机的购买数量不少于6部且不多于8部,请你求出商场每种型号手机的购买数量.
28.(本题6分)
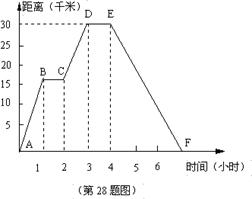
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家12千米?
29.(本题9分)
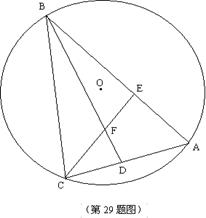
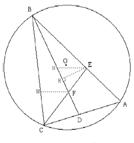
如图:已知,△ABC内接于⊙O,弦BC所对的劣弧为1200,∠ABC、∠ACB的平分线BD、CE分别交AC于D,交AB于E,BD、CE相交于点F.
(1)求cot∠EFB的值;
(2)EF=DF;
(3)当BF=3EF,且线段BF、CF的长是关于x的方程x2-(2m+6)x+2m2=0(m>0)的两个实数根时,求AB的长.
30.(本题10分)
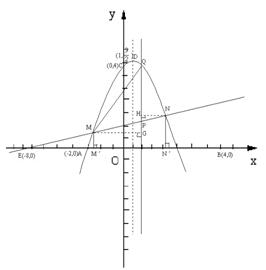
![]() 已知:抛物线y=- x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
已知:抛物线y=- x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线的解析式;
(2)在x轴上,点A的左侧,求一点E,使△ECO与△CAO相似,并说明直线EC经过(1)中抛物线的顶点D;
(3)过(2)中的点E的直线y=![]() x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M'、N',点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形 MM'N'N:S△QMN=35:12,若存在,求出满足条件的t值;若不存在,请说明理由.
x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M'、N',点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形 MM'N'N:S△QMN=35:12,若存在,求出满足条件的t值;若不存在,请说明理由.
哈尔滨市2004年初中升学考试数学试题
参考答案及评分标准
一、单项选择题(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | B | D | B | B | C | A | C |
二、填空题(每小题3分,共30分)
11.1.17×105;
12. ![]() ; 13.(a-b-c); 14.3<x≤5; 15.30;
; 13.(a-b-c); 14.3<x≤5; 15.30;
16.70;
17.(n+2)2-n2=4(n+1); 18.k<0; 19.1440; 20. ![]() 或
或![]() 者 .
者 .
![]() 三、解答题(其中21题4分,22题5分,23题4分,24—25题各5分,26—28题各6分,29题9分,30题10分,共60分)
三、解答题(其中21题4分,22题5分,23题4分,24—25题各5分,26—28题各6分,29题9分,30题10分,共60分)
21.解:原式= ………………………………………………(1分)
![]()
= …………………………………………………………………………………(1分)
x=tan450-cot300=1-![]() 时,………………………………………………………………………(1分)
时,………………………………………………………………………(1分)
![]()
![]()
原式= = …………………………………………………………………………………(1分)
22.解:设x2+2x=y,则原式可化成y2-2y-3=0,………………………………………………………(1分)
解得y1=3,y2=-1……………………………………………………………………………… (1分)
当y=3时,x2+2x-3=0,解得x1=-3,x2=1……………………………………………………(1分)
当y=-1时,x2+2x-3=0,解得x3= x4=-1………………………………………………………(1分)
经检验x1=-3,x2=1,x3= x4=-1都是原方程的根
∴原方程的根是x1=-3,x2=1,x3= x4=-1………………………………………………………(1分)
23.证明:连结BE
|
|
|



| ||||
| ||||
∴AB CD,AO=OC…………………………………(1分)
| ||||
| ||||
∵CE=CD,∴AB CE,
∴四边形ABEC为平行四边形,………………… (1分)
|
∴BF=FC,………………………………………… (1分)
|
∴OF ![]() AB,即:AB=2OF.……………………… (1分)
AB,即:AB=2OF.……………………… (1分)
24.解:由题意可知:EG、CD、30,
∵∠AEG=300,∠AGF=600 ∴∠EAG=300, ∴EG=AG=30…………………………………(1分)
在Rt△AFG中,sin600=![]() ,……………………………………………………………………(1分)
,……………………………………………………………………(1分)
![]() ∴AF=AG·sin600=30×
∴AF=AG·sin600=30×![]() =15 (米)……………………………………………………………(1分)
=15 (米)……………………………………………………………(1分)
![]()
![]() ∴AB、AF+FB=(15 +
∴AB、AF+FB=(15 + ![]() )米……………………………………………………………………(1分)
)米……………………………………………………………………(1分)
![]() 答:塔高AB为(15 + )米.
……………………………………………………………… (1分)
答:塔高AB为(15 + )米.
……………………………………………………………… (1分)
25.解:(1)因为频率之比等于频数之比,
设第一小组的频数为2k,所以各组的频数依次为2k、4k、9k、7k、3k,
于是3k=30,所以k=10. ……………………………………………………………………………(1分)
所以2k=20,4k=40,9k=90,7k=70,所以20+40+90+70+30=250(人).
答:本次调查共抽测了250名学生. ………………………………………………………………(1分)
(2)中位数应在第三小组. ………………………………………………………………………(1分)
∵250个数据的中位数是第125和第126两个数据的平均数,
前两个小组的频数之和是20+40=60,60<125
第三小组的频数是90,90+60=150,150>126,
∴中位数应在第三小组. ……………………………………………………………………(1分)
(3)∵视力在4.9—5.1范围内的人有70人,
∴频率=![]() =0.28,
=0.28,
∴全市初中生视力正常的约有40000×0.28=11200(人),
答:全市初中生视力正常的约有11200人. ………………………………………………………(1分)
26.(1)∵BE是⊙O1的直径, ∴∠BPE=900, ∵BF┴O1P,∴∠BPF+∠FBP=900,
∵∠GPF+∠BPF=900, ∴∠GPF=∠BPF,……………………………………………………(1分)
∵O1E= O1P, ∴∠E=∠GPF=∠PBF,
又∵∠BPG=∠EPB=900, ∴△GPB∽△BPE,
∴![]() ,∴PB2=PE·PG. …………………………………………………………………(1分)
,∴PB2=PE·PG. …………………………………………………………………(1分)
(2)∵AB是⊙O1的切线, ∴O1B┴AB, ∴△O1BF∽△O1AB, ∴∠O1BF=∠A,
![]() ∵tan∠A=
∵tan∠A=![]() , ∴tan∠O1BF= ,……………………………………………………(1分)
, ∴tan∠O1BF= ,……………………………………………………(1分)
设O1F=3m,则BF=4m,由勾股定理得:O1B=5m=O1P, ∴PF=5m-3m=2m,
![]() 又∵PF=
又∵PF=![]() ,∴m= ,…………………………………………………………………………(1分)
,∴m= ,…………………………………………………………………………(1分)
![]()
![]() ∴O1B=O1P=
∴O1B=O1P=![]() ,∵tan∠A= ,BF=4m,∴AF=
,∵tan∠A= ,BF=4m,∴AF=![]() m,AP= m-2m=
m,AP= m-2m= ![]() m=
m= ![]() ,
,
![]()
![]() ∴PO2=
∴PO2= ![]() ,∴O1O2= + =5. ……………………………………………………………(1分)
,∴O1O2= + =5. ……………………………………………………………(1分)
27.解:(1)设甲种型号手机要购买x部,乙种型号手机购买y部,丙种型号手机购买z部,
 根据题意,得:
………………(1分)
根据题意,得:
………………(1分)
………………(1分)
答:有两种购买方法:甲种手机购买30部,乙种手机购买10部;或甲种手机购买20部,乙种手机购买20部. …………………………………………………………………………………(1分)
(2)根据题意,得:![]() ………………………………………(1分)
………………………………………(1分)
解得:![]() ………………………………………………(1分)
………………………………………………(1分)
答:若甲种型号手机购买26部手,则乙种型号手机购买6部,丙种型号手机购买8部;
若甲种型号手机购买27部手,则乙种型号手机购买7部,丙种型号手机购买6部;
若甲种型号手机购买28部手,则乙种型号手机购买8部,丙种型号手机购买4部;
………………………………………………………………………………………………… (1分)
28.解:(1)由图象可知小明到达离家最远的地方需3小时;此时,他离家30千米.………… (1分)(2)设直线CD的解析式为y=k1x+b1,由C(2,15)、D(3,30),
代入得:y=15x-15,(2≤x≤3)…………………………………………………………(1分)
当x=2.5时,y=22.5(千米)答:出发两个半小时,小明离家22.5千米. ………(1分)
(3)设过E、F两点的直线解析式为y=k2x+b2,
由E(4,30)、F(6,0),代入得y=-15x+90,(4≤x≤6)……………………………(1分)
过A、B两点的直线解析式为y=k3x,∵B(1,15) ∴y=15x.(0≤x≤1) ………(1分)
![]() 分别令y=12,得x=
分别令y=12,得x=![]() (小时),x=
(小时),x=![]() (小时).
(小时).
![]() 答:小明出发 小时或 小时距家12千米. ………………………………………………(1分)
答:小明出发 小时或 小时距家12千米. ………………………………………………(1分)
29.解:(1)∵![]() 为1200,∴∠A=600,∴∠ABC+∠ACB=1200,……………………………………(1分)
为1200,∴∠A=600,∴∠ABC+∠ACB=1200,……………………………………(1分)
![]() ∵BD、CE平分∠ABC和∠ACB,∴
∵BD、CE平分∠ABC和∠ACB,∴![]() ∠ABC+ ∠ACB=600=∠BFE,
∠ABC+ ∠ACB=600=∠BFE,
![]() ∴cot600= . ………………………………………………………………………… (1分)
∴cot600= . ………………………………………………………………………… (1分)
 (2)作∠BFC的平分线FM交BC于点M,
(2)作∠BFC的平分线FM交BC于点M,
则∠BFM=∠CFM=600,
在△BFM与△BFE中,![]()
∴△BFM≌△BFE中,……………………………(1分)
∴MF=EF.
同理可证:△CFM≌△CDF,…………………… (1分)
∴MF=DF,∴EF=DF,…………………………… (1分)
(3)设EF=k,则BF=3k,在BF上截取FN=EF=k,
则BN=2k,△FEN为等边三角形,
∴EN=EF=k,∴∠BNE=1200,∴△BNE∽△BFC,
![]() ∴
∴![]() ,∴CF= ,……………………………………………………………(1分)
,∴CF= ,……………………………………………………………(1分)
∵BF、CF的长是方程x2-(2m+6)x+2m2=0的两个实数根,由根与系数的关系可知:
![]()
![]() BF+CF=3k+ =2m+6, BF·CF= =2m2,
BF+CF=3k+ =2m+6, BF·CF= =2m2,
![]() 联立,消去k得5m2-24m-36=0,解得:m1=6,m2=-
联立,消去k得5m2-24m-36=0,解得:m1=6,m2=-![]() , ∵m>0, ∴m=- (舍). ……(1分)
, ∵m>0, ∴m=- (舍). ……(1分)
当m=6时,方程为x2-18x+72=0,解得:x1=12=BF,x2=6=CF, ∴EF=4.
过点E作EH┴BF于H,则FH=2,由勾股定理得:EH=![]() ,BH=12-2=10,
,BH=12-2=10,
由勾股定理得:BE=![]() ,…………………………………………………(1分)
,…………………………………………………(1分)
∵△BFE∽△BAD,∴![]() ,
,
∴AB=![]() . ……………………………………………………(1分)
. ……………………………………………………(1分)
30.解:(1) ∵x1<0,x2>0, ∴OA=x1,OB=x2,
![]() ∵x1,x2是方程 - x2-(m+3)x+m2-12=0的两个实数根,
∵x1,x2是方程 - x2-(m+3)x+m2-12=0的两个实数根,
由根与系数关系得:x1+x2=-2(m+3)①x1·x2=-2(m2-12) ②x2=-2x1③………… (1分)
联立,整理,得:m2+8m+16=0,解得:m1=m2=-4,……………………………… (1分)
 ∴抛物线的解析式为y=-
∴抛物线的解析式为y=-![]() x2+x+4. ……………………………………………………(1分)
x2+x+4. ……………………………………………………(1分)
(2)设点E(x,0),则OE=-x,
∵△ECO与△CAO相似,
∴![]() ∴
∴![]() ∴x=-8
∴x=-8
∴点E(-8,0),…………………………………(1分)
设过E、C两点的直线解析式为y=k′x+b′
由题意得:![]()
所以直线EC的解析式为:y=![]() x+4……… (1分)
x+4……… (1分)
∵抛物线的顶点D(1,![]() ),当x=1时,y=
),当x=1时,y=![]() ,
,
∴点D在直线EC上. ………………(1分)
(3)存在t值,使S梯形MM′N′N:S△QMN=35:12. ………………(1分)
∵E(-8,0),∴0=![]() ×(-8)+b,∴b=2,
×(-8)+b,∴b=2,
![]() ∴y= x+2, ∴x=4(y-2),
∴y= x+2, ∴x=4(y-2),
![]() ∴y=- ×[4(y-2)]2+4(y-2)+4,整理得:8y2-35y+6=0,设M(xm,ym)、N(xn,yn),
∴y=- ×[4(y-2)]2+4(y-2)+4,整理得:8y2-35y+6=0,设M(xm,ym)、N(xn,yn),
∴MM′=ym,NN′=yn, ∴ym、yn是方程8y2-35y+6=0的两个实数根,
∴ym+yn=![]() ,……………………………………………………………………………(1分)
,……………………………………………………………………………(1分)
![]() ∴S梯形MM′N′N= (ym+yn)(xn-xm),
∴S梯形MM′N′N= (ym+yn)(xn-xm),
![]() ∵点P在直线y= x+2上,点Q在(1)中抛物线上
∵点P在直线y= x+2上,点Q在(1)中抛物线上
![]()
![]() ∴点P(t, +2)、点Q(t, -
t2+t+4),
∴点P(t, +2)、点Q(t, -
t2+t+4),
![]()
![]()
![]()
![]()
![]() ∴PQ=- t2+t+4-
t-2=- t2+ t+2,
∴PQ=- t2+t+4-
t-2=- t2+ t+2,
分别过M、N作直线PQ的垂线,垂足为G、H,则GM=t-xm,NH=xn-t,
![]() ∴S△QMN= S△QMP+S△QNP= PQ(xn-xm),
∴S△QMN= S△QMP+S△QNP= PQ(xn-xm),
∵S梯形MM′N′N:S△QMN=35:12
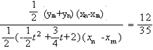
∴ …………………………………………………………… (1分)
∴![]() (-
(-![]() t2+
t2+![]() t+2),
t+2),
![]() 整理,得:2t2-3t-2=0,解得:t1=- ,t2=2,
整理,得:2t2-3t-2=0,解得:t1=- ,t2=2,
![]() ∴当t=- 或t=2时,S梯形MM′N′N:S△QMN=35:12. …………………………………………(1分)
∴当t=- 或t=2时,S梯形MM′N′N:S△QMN=35:12. …………………………………………(1分)
注:有不同于本评分标准的正确答案,可按相应的解题步骤给分.