闵行区2002年中等学校分流招生考试
数 学 试 题
（120分钟完成，满分120分）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 总 分 |
| 得 分 |
一、填空题（本题共14小题，每小题2分，满分28分）
1．计算：
______________.
2．用科学记数法表示：0.00034
____________.
3．分解因式：
____________________.
4．函数
的定义域是________________.
5．如果函数
，那么
________.
6．如果反比例函数的图象经过点
，那么这个函数的解析式为___________.
7．如果一元二次方程
的两根之和为
，则两根之积为
__________.
8．如果方程
有一个实数根是2，那么k __________.
9．一个学习小组有9人，在一次数学测验中，得100分的有2人，得90分的有2 人，
得80分的有4人，得65分的有1人，那么这个小组在这次数学测验中的平均成绩
是_____________分.
10.对角线长分别为6cm和8cm的菱形的边长为_____________cm.
11.已知梯形的上底长为3cm，中位线长为5cm，那么下底长为______________cm.
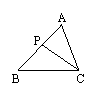12.如图，已知⊿ABC中，P是AB边上一点，连结PC，
要使⊿ACP ∽⊿ABC，只需添加条件_____________.
(只要写出一种适合的条件)
13.在Rt⊿ABC中，
，如果AB = 6，
，那么BC = __________.
14.两圆半径分别为3和5，d表示这两圆的圆心距，当
时，这两圆的位置关
系是__________________.
二、单项选择题（本题共4小题，每小题3分，满分12分）
15.下列计算正确的是………………………………………………………………（ ）
16.抛物线
的对称轴是直线 ……………………………………（ ）
17.某学校有数学教师25名，将他们的年龄分成3组，在38～45(岁)组内有8名教师，
那么这个小组的频率是…………………………………………………………（ ）
18.下列命题中，错误的命题是……………………………………………………（ ）
所有的等边三角形都是彼此相似的三角形
所有的矩形都是彼此相似的四边形
所有的等腰直角三角形都是彼此相似的三角形
有两组对应边成比例的直角三角形相似
三、（本题共4小题，每小题7分，满分28分）
19．解不等式组：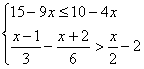
20．解方程：
21．我区某学校组织高一学生到学农基地进行学农劳动，基地分配给该学校宿舍若
干．如果每室住8人，则少12个床位，如果每室住9人，却又空出2个房间．
问该学校参加这次学农的学生有多少人？基地分配给学校宿舍有几间？
22．已知：如图，在平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，平行四边
形 ABCD的周长为28，面积为40， AB∶AD = 4∶3．
求(1) DE的长；
(2)
的值．
四、（本题共4小题，每小题10分，满分40分）
23．已知直线
经过点A(0，6)，且平行于直线
．
(1) 求k、b的值；
(2) 如果这条直线经过点P（m，2），求m的值；
(3) 写出表示直线OP的函数解析式；
(4) 求由直线，直线OP与x轴围成的图形的面积．
24. 在⊿ABC中，∠ACB = 90°，以AC为直径的圆交斜边AB于点P．E是BC的中
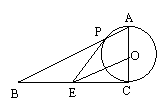点，连结PE．
(1) 如果圆O的半径为2，∠B =30°，求OE的长．
(2) 求证：PE是⊙O的切线．
25．如图，在⊿ABC中，AQ=PQ，PR=PS，
PS⊥AC于S，PR⊥AB于R，则三个结论：
①AS=AR；②⊿BRP ∽⊿QSP；③PQ∥AB中，
正确的是____________．
请证明你所得到的结论．
26.已知抛物线
上有A、B两点，它们的横坐标分别为 -1，2．如果
⊿AOB（O是坐标原点）是直角三角形，求a的值．
五、（本题满分12分）
27．如图，在梯形ABCD中，AD‖BC，
∠BAD=90°，AD+AB=14，（AB>AD）
BD=10， BD =DC，E、F分别是BC、
CD上的点，且CE+CF = 4．
(1) 求BC的长；
(2) 设EC的长为x，四边形AEFD的面积为y，求y关于x的函数关系式，并写
出函数的定义域；
(3) 在(2)的条件下，如果四边形AEFD的面积等于40，试求EC的长．