《二次根式》提高测试
(一)判断题:(每小题1分,共5分)
1.![]() =-2
=-2![]() .…………………( )【提示】
.…………………( )【提示】![]() =-2=2.【答案】×.
=-2=2.【答案】×.
2.![]() -2的倒数是
-2的倒数是![]() +2.( )【提示】
+2.( )【提示】![]() =
=![]() =-(
=-(![]() +2).【答案】×.
+2).【答案】×.
3.![]() =
=![]() .…( )【提示】
.…( )【提示】![]() =x-1,
=x-1,![]() =x-1(x≥1).两式相等,必须x≥1.但等式左边x可取任何数.【答案】×.
=x-1(x≥1).两式相等,必须x≥1.但等式左边x可取任何数.【答案】×.
4.![]() 、
、![]()
![]() 、
、![]() 是同类二次根式.…( )【提示】
是同类二次根式.…( )【提示】![]()
![]() 、
、![]() 化成最简二次根式后再判断.【答案】√.
化成最简二次根式后再判断.【答案】√.
5.![]() ,
,![]() ,
,![]() 都不是最简二次根式.( )
都不是最简二次根式.( )![]() 是最简二次根式.【答案】×.
是最简二次根式.【答案】×.
(二)填空题:(每小题2分,共20分)
6.当x__________时,式子![]() 有意义.【提示】
有意义.【提示】![]() 何时有意义?x≥0.分式何时有意义?分母不等于零.【答案】x≥0且x≠9.
何时有意义?x≥0.分式何时有意义?分母不等于零.【答案】x≥0且x≠9.
7.化简-![]()
![]() ÷
÷![]() =_.【答案】-2a
=_.【答案】-2a![]() .【点评】注意除法法则和积的算术平方根性质的运用.
.【点评】注意除法法则和积的算术平方根性质的运用.
8.a-![]() 的有理化因式是____________.【提示】(a-
的有理化因式是____________.【提示】(a-![]() )(________)=a2-
)(________)=a2-![]() .a+
.a+![]() .【答案】a+
.【答案】a+![]() .
.
9.当1<x<4时,x-4+![]() =________________.
=________________.
【提示】x2-2x+1=( )2,x-1.当1<x<4时,x-4,x-1是正数还是负数?
x-4是负数,x-1是正数.【答案】3.
10.方程![]() (x-1)=x+1的解是____________.【提示】把方程整理成ax=b的形式后,a、b分别是多少?
(x-1)=x+1的解是____________.【提示】把方程整理成ax=b的形式后,a、b分别是多少?![]() ,
,![]() .【答案】x=3+2
.【答案】x=3+2![]() .
.
11.已知a、b、c为正数,d为负数,化简![]() =______.【提示】
=______.【提示】![]() =cd=-cd.
=cd=-cd.
【答案】![]() +cd.【点评】∵ ab=
+cd.【点评】∵ ab=![]() (ab>0),∴ ab-c2d2=(
(ab>0),∴ ab-c2d2=(![]() )(
)(![]() ).
).
12.比较大小:-![]() _________-
_________-![]() .【提示】2
.【提示】2![]() =
=![]() ,4
,4![]() =
=![]() .
.
【答案】<.【点评】先比较![]() ,
,![]() 的大小,再比较
的大小,再比较![]() ,
,![]() 的大小,最后比较-
的大小,最后比较-![]() 与-
与-![]() 的大小.
的大小.
13.化简:(7-5![]() )2000·(-7-5
)2000·(-7-5![]() )2001=______________.
)2001=______________.
【提示】(-7-5![]() )2001=(-7-5
)2001=(-7-5![]() )2000·(_________)[-7-5
)2000·(_________)[-7-5![]() .]
.]
(7-5![]() )·(-7-5
)·(-7-5![]() )=?[1.]【答案】-7-5
)=?[1.]【答案】-7-5![]() .
.
【点评】注意在化简过程中运用幂的运算法则和平方差公式.
14.若![]() +
+![]() =0,则(x-1)2+(y+3)2=____________.【答案】40.
=0,则(x-1)2+(y+3)2=____________.【答案】40.
【点评】![]() ≥0,
≥0,![]() ≥0.当
≥0.当![]() +
+![]() =0时,x+1=0,y-3=0.
=0时,x+1=0,y-3=0.
15.x,y分别为8-![]() 的整数部分和小数部分,则2xy-y2=____________.
的整数部分和小数部分,则2xy-y2=____________.
【提示】∵ 3<![]() <4,∴ _______<8-
<4,∴ _______<8-![]() <__________.[4,5].由于8-
<__________.[4,5].由于8-![]() 介于4与5之间,则其整数部分x=?小数部分y=?[x=4,y=4-
介于4与5之间,则其整数部分x=?小数部分y=?[x=4,y=4-![]() ]【答案】5.
]【答案】5.
【点评】求二次根式的整数部分和小数部分时,先要对无理数进行估算.在明确了二次根式的取值范围后,其整数部分和小数部分就不难确定了.
(三)选择题:(每小题3分,共15分)
16.已知![]() =-x
=-x![]() ,则………………( )
,则………………( )
(A)x≤0 (B)x≤-3 (C)x≥-3 (D)-3≤x≤0【答案】D.
【点评】本题考查积的算术平方根性质成立的条件,(A)、(C)不正确是因为只考虑了其中一个算术平方根的意义.
17.若x<y<0,则![]() +
+![]() =………………………( )
=………………………( )
(A)2x (B)2y (C)-2x (D)-2y
【提示】∵ x<y<0,∴ x-y<0,x+y<0.
∴ ![]() =
=![]() =x-y=y-x.
=x-y=y-x.
![]() =
=![]() =x+y=-x-y.【答案】C.
=x+y=-x-y.【答案】C.
【点评】本题考查二次根式的性质![]() =a.
=a.
18.若0<x<1,则![]() -
-![]() 等于………………………( )
等于………………………( )
(A)![]() (B)-
(B)-![]() (C)-2x (D)2x
(C)-2x (D)2x
【提示】(x-![]() )2+4=(x+
)2+4=(x+![]() )2,(x+
)2,(x+![]() )2-4=(x-
)2-4=(x-![]() )2.又∵ 0<x<1,
)2.又∵ 0<x<1,
∴ x+![]() >0,x-
>0,x-![]() <0.【答案】D.
<0.【答案】D.
【点评】本题考查完全平方公式和二次根式的性质.(A)不正确是因为用性质时没有注意当0<x<1时,x-![]() <0.
<0.
19.化简![]()
![]() a<0
a<0![]() 得………………………………………………………………( )
得………………………………………………………………( )
(A)![]() (B)-
(B)-![]() (C)-
(C)-![]() (D)
(D)![]()
【提示】![]() =
=![]() =
=![]() ·
·![]() =a
=a![]() =-a
=-a![]() .【答案】C.
.【答案】C.
20.当a<0,b<0时,-a+2![]() -b可变形为………………………………………( )
-b可变形为………………………………………( )
(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)
(D)![]()
【提示】∵ a<0,b<0,
∴ -a>0,-b>0.并且-a=![]() ,-b=
,-b=![]() ,
,![]() =
=![]() .
.
【答案】C.【点评】本题考查逆向运用公式![]() =a(a≥0)和完全平方公式.注意(A)、(B)不正确是因为a<0,b<0时,
=a(a≥0)和完全平方公式.注意(A)、(B)不正确是因为a<0,b<0时,![]() 、
、![]() 都没有意义.
都没有意义.
(四)在实数范围内因式分解:(每小题3分,共6分)
21.9x2-5y2;【提示】用平方差公式分解,并注意到5y2=![]() .【答案】(3x+
.【答案】(3x+![]() y)(3x-
y)(3x-![]() y).
y).
22.4x4-4x2+1.【提示】先用完全平方公式,再用平方差公式分解.【答案】(![]() x+1)2(
x+1)2(![]() x-1)2.
x-1)2.
(五)计算题:(每小题6分,共24分)
23.(![]() )(
)(![]() );
);
【提示】将![]() 看成一个整体,先用平方差公式,再用完全平方公式.
看成一个整体,先用平方差公式,再用完全平方公式.
【解】原式=(![]() )2-
)2-![]() =5-2
=5-2![]() +3-2=6-2
+3-2=6-2![]() .
.
24.![]() -
-![]() -
-![]() ;【提示】先分别分母有理化,再合并同类二次根式.
;【提示】先分别分母有理化,再合并同类二次根式.
【解】原式=![]() -
-![]() -
-![]() =4+
=4+![]() -
-![]() -
-![]() -3+
-3+![]() =1.
=1.
25.(a2![]() -
-![]()
![]() +
+![]()
![]() )÷a2b2
)÷a2b2![]() ;
;
【提示】先将除法转化为乘法,再用乘法分配律展开,最后合并同类二次根式.
【解】原式=(a2![]() -
-![]()
![]() +
+![]()
![]() )·
)·![]()
![]()
=![]()
![]() -
-![]()
![]() +
+![]()
![]()
=![]() -
-![]() +
+![]() =
=![]() .
.
26.(![]() +
+![]() )÷(
)÷(![]() +
+![]() -
-![]() )(a≠b).
)(a≠b).
【提示】本题应先将两个括号内的分式分别通分,然后分解因式并约分.
【解】原式=![]() ÷
÷![]()
=![]() ÷
÷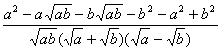
=![]() ·
·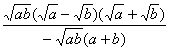 =-
=-![]() .
.
【点评】本题如果先分母有理化,那么计算较烦琐.
(六)求值:(每小题7分,共14分)
27.已知x=![]() ,y=
,y=![]() ,求
,求![]() 的值.
的值.
【提示】先将已知条件化简,再将分式化简最后将已知条件代入求值.
【解】∵ x=![]() =
=![]() =5+2
=5+2![]() ,
,
y=![]() =
=![]() =5-2
=5-2![]() .
.
∴ x+y=10,x-y=4![]() ,xy=52-(2
,xy=52-(2![]() )2=1.
)2=1.
![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
【点评】本题将x、y化简后,根据解题的需要,先分别求出“x+y”、“x-y”、“xy”.从而使求值的过程更简捷.
28.当x=1-![]() 时,求
时,求![]() +
+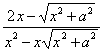 +
+![]() 的值.
的值.
【提示】注意:x2+a2=![]() ,
,
∴ x2+a2-x![]() =
=![]() (
(![]() -x),x2-x
-x),x2-x![]() =-x(
=-x(![]() -x).
-x).
【解】原式=![]() -
-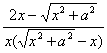 +
+![]()
=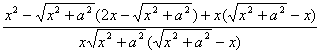
=![]() =
=![]() =
=![]()
=![]() .当x=1-
.当x=1-![]() 时,原式=
时,原式=![]() =-1-
=-1-![]() .【点评】本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=
.【点评】本题如果将前两个“分式”分拆成两个“分式”之差,那么化简会更简便.即原式=![]() -
-![]() +
+![]()
=![]() -
-![]() +
+![]() =
=![]() .
.
七、解答题:(每小题8分,共16分)
29.计算(2![]() +1)(
+1)(![]() +
+![]() +
+![]() +…+
+…+![]() ).
).
【提示】先将每个部分分母有理化后,再计算.
【解】原式=(2![]() +1)(
+1)(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
=(2![]() +1)[(
+1)[(![]() )+(
)+(![]() )+(
)+(![]() )+…+(
)+…+(![]() )]
)]
=(2![]() +1)(
+1)(![]() )
)
=9(2![]() +1).
+1).
【点评】本题第二个括号内有99个不同分母,不可能通分.这里采用的是先分母有理化,将分母化为整数,从而使每一项转化成两数之差,然后逐项相消.这种方法也叫做裂项相消法.
30.若x,y为实数,且y=![]() +
+![]() +
+![]() .求
.求![]() -
-![]() 的值.
的值.
【提示】要使y有意义,必须满足什么条件?![]() 你能求出x,y的值吗?
你能求出x,y的值吗?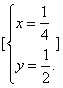
【解】要使y有意义,必须![]() ,即
,即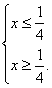 ∴ x=
∴ x=![]() .当x=
.当x=![]() 时,y=
时,y=![]() .
.
又∵ ![]() -
-![]() =
=![]() -
-![]()
=![]() -
-![]() ∵ x=
∵ x=![]() ,y=
,y=![]() ,∴
,∴ ![]() <
<![]() .
.
∴ 原式=![]() -
-![]() =2
=2![]() 当x=
当x=![]() ,y=
,y=![]() 时,
时,
原式=2![]() =
=![]() .【点评】解本题的关键是利用二次根式的意义求出x的值,进而求出y的值.
.【点评】解本题的关键是利用二次根式的意义求出x的值,进而求出y的值.