中考数学试题分类汇编（解直角三角形）含答案
一、选择题
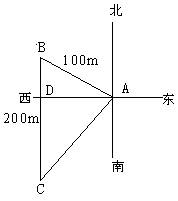
1、（2007山东淄博）王英同学从A地沿北偏西60º方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地 （ ）D
（A）
m （B）100 m
（C）150m （D）
m
解：作出如图所示图形，则∠BAD＝90°－60°＝30°，AB＝100，所以BD＝50，cos30°＝
，所以，AD＝50
，
CD＝200－50＝150，在Rt△ADC中，
AC＝
＝
＝100，故选（D）。
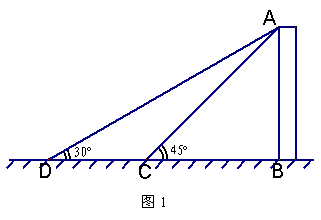
2、（2007浙江杭州）如图1，在高楼前
点测得楼顶的仰角为
，向高楼前进60米到
点，又测得仰角为
，则该高楼的高度大约为（ ）A
A.82米 B.163米 C.52米 D.70米
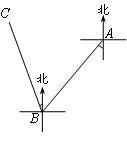3、（2007南充）一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地，再由B地向北偏西10º的方向行驶40海里到达C地，则A、C两地相距（ ）．B
（A）30海里 （B）40海里 （C）50海里 （D）60海里
4、（2007江苏盐城）利用计算器求sin30°时，依次按键
则计算器上显示的结果是( )A
A．0．5 B．0．707 C．0．866 D．1
5、(2007山东东营)王英同学从A地沿北偏西60º方向走100m到B地，再从B地向正南方向走200m到C地，此时王英同学离A地 ( )D
（A）150m （B）m
（C）100 m （D）m
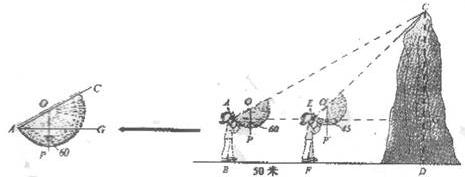
6、（2007浙江台州）一次数学活动中，小迪利用自己制作的测角器测量小山的高度
．已知她的眼睛与地面的距离为1.6米，小迪在
处测量时，测角器中的
（量角器零度线
和铅垂线
的夹角，如图）；然后她向小山走50米到达点
处（点
在同一直线上），这时测角器中的
，那么小山的高度约为（ ）
Ａ．68米 Ｂ．70米 Ｃ．121米 Ｄ．123米
（注：数据
，
供计算时选用）
B
二、填空题
1、（2007山东济宁）计算
的值是
。0
2、（2007湖北黄冈）计算：2sin60°=
.
3、（2007湖北省天门）化简
＝（ ）。A
A、
B、
C、
D、
三、解答题
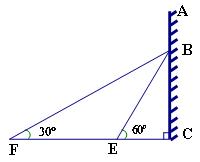1、（2007云南双柏县）如图，在某建筑物AC上，挂着“多彩云南”的宣传条幅BC，小明站在点F处，看条幅顶端B，测的仰角为
，再往条幅方向前行20米到达点E处，看到条幅顶端B，测的仰角为
，求宣传条幅BC的长，（小明的身高不计，结果精确到0.1米）
解： ∵∠BFC =，∠BEC =，∠BCF =
∴∠EBF =∠EBC =
∴BE = EF = 20
在Rt⊿BCE中，
答：宣传条幅BC的长是17.3米。
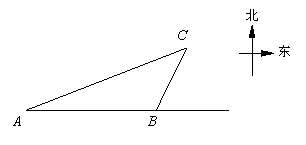
2、（2007山东青岛）一艘轮船自西向东航行，在A处测得东偏北21.3°方向有一座小岛C，继续向东航行60海里到达B处，测得小岛C此时在轮船的东偏北63.5°方向上．之后，轮船继续向东航行多少海里，距离小岛C最近？
（参考数据：sin21.3°≈
，tan21.3°≈
， sin63.5°≈
，tan63.5°≈2）
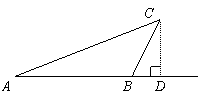解：过C作AB的垂线，交直线AB于点D，得到Rt△ACD与Rt△BCD．
设BD＝x海里，
在Rt△BCD中，tan∠CBD＝
，
∴CD＝x ·tan63.5°．
在Rt△ACD中，AD＝AB＋BD＝(60＋x)海里，tan∠A＝
，
∴CD＝( 60＋x ) ·tan21.3°．
∴x·tan63.5°＝(60＋x)·tan21.3°，即 
．
解得，x＝15．
答：轮船继续向东航行15海里，距离小岛C最近
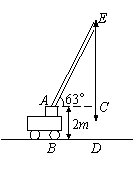
3、（2007福建晋江）如图所示，一辆吊车的吊臂以63°的倾角倾斜于水
平面，如果这辆吊车支点A距地面的高度AB为2m，且点A到铅
垂线ED的距离为AC＝15m，求吊臂的最高点E到地面的高度ED
的长（精确到0.1 m）。
答案：31.4m；
4、（2007湖南怀化）九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度
，标杆与旗杆的水平距离
，人的眼睛与地面的高度
，人与标杆的水平距离
，求旗杆
的高度．
解：
，
，
，即：
，
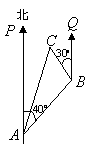
5、（2007山东威海）如图，一条小船从港口
出发，沿北偏东
方向航行
海里后到达处，然后又沿北偏西
方向航行
海里后到达
处．问此时小船距港口多少海里？（结果精确到1海里）
友情提示：以下数据可以选用：
，
，
，
．
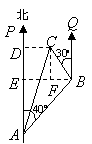
解：过点作
，垂足为点
；过点分别作
，
，垂足分别为点
，则四边形
为矩形．
，…………………………3分
，
．
，
；
．
，
；
．
．
，
．
由勾股定理，得
．
即此时小船距港口约25海里
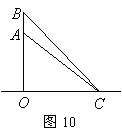6、（2007贵州贵阳）如图10，一枚运载火箭从地面
处发射，当火箭到达点时，从地面处的雷达站测得的距离是
，仰角是
．
后，火箭到达点，此时测得
的距离是
，仰角为
，解答下列问题：
（1）火箭到达点时距离发射点有多远（精确到0.01km）？（4分）
（2）火箭从点到点的平均速度是多少（精确到0.1km/s）？（6分）
（1）在
中，
····················· 1分
（km）······················ 3分
火箭到达点时距发射点约
············································································· 4分
（2）在
中，
············································································ 1分
························································································ 3分
······················································ 5分
答：火箭从点到点的平均速度约为
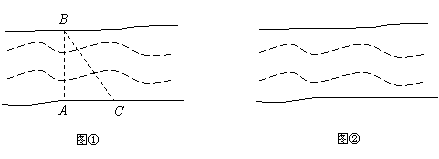
7、（2007湖北潜江）经过江汉平原的沪蓉(上海—成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①，一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得
.
（1）求所测之处江的宽度（
）；
（2）除(1)的测量方案外，请你再设计一种测量江宽的方案，并在图②中画出图形.
 |
解：（1）在
中，，
∴
（米）
答：所测之处江的宽度约为248米……………………………………………………（3分）
（2）从所画出的图形中可以看出是利用三角形全等、三角形相似、解直角三角形的知识
来解决问题的，只要正确即可得分
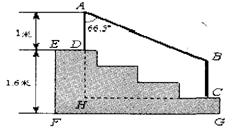8、（2007苏州）某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为l.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D，C)，且∠DAB=66. 5°．
(1)求点D与点C的高度差DH；
(2)求所用不锈钢材料的总长度
(即AD+AB+BC，结果精确到0.1米)．(参考数据：sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30)
解：(1)DH=1.6×
=l.2(米)．(2)过B作BM⊥AH于M，则四边形BCHM是矩形．
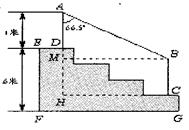MH=BC=1 ∴AM=AH-MH=1+1.2一l=l.2．
在RtAMB中，∵∠A=66.5°
∴AB=
(米)．
∴S=AD+AB+BC≈1+3.0+1=5.0(米)．
答：点D与点C的高度差DH为l.2米；所用不锈钢材料的总长度约为5.0米