初三数学第一学期夜课甲班练习（8）

初三数学第一学期夜课甲班练习（8）　　　　姓名：____________

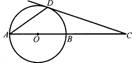1．如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切，切点为D。如果∠A=35°，那么∠C等于

A、20°　　 B、30°　　 C、35°　　 D、55°

2．如果正n边形的一个内角等于一个外角的2倍，那么n的值是

A、4　　 B、5　　 C、6　　　D、7

3．在函数中，自变量x的取值范围是

A、x≠3　　 B、x≠0　　 C、x＞3　　 D、x≠－3

4．小芸所在学习小组的同学们，响应“为祖国争光，为奥运添彩”的号召，主动到附近的7个社区帮助爷爷、奶奶们学习英语日常用语。他们记录的各社区参加其中一次活动的人数如下：33，32，32，31，28，26，32，那么这组数据的众数和中位数分别是

A、32，31　　 B、32，32　　 C、3，31　　 D、3，32

5．下午2点30分时（如图），时钟的分针与时针所成角的度数为

A．90°　　　　　　　　　　　　　　　　　　　 B．105°

C．120°　　　　　　　　　　　　　　　　　　 D．135°

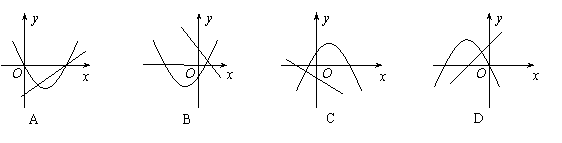6．在同一平面直角坐标系中，一次函数和二次函数的图象可能为

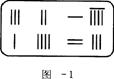
7．《九章算术》是我国东汉初年编订的一部数学经典著作．在它的“方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图3－1、图3－2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图3－1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是类似地，图3－2所示的算筹图我们可以表述为

A．　 B．　 C．　 D．

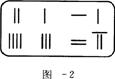
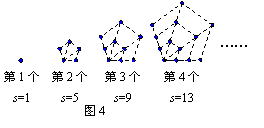8．观察图4给出的四个点阵，s表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n个点阵中的点的个数s为

A．3n－2 　　　　　　　　B．3n－1

C．4n＋1 　　　　　　　 D．4n－3

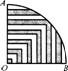
9．将如右图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计)，则围成的圆锥形纸帽是

　　　　

11．如果，，那么的值等于　　　　　  。

12．用“☆”定义新运算： 对于任意实数a、b， 都有a☆b=b²＋1。 例如7☆4=4²＋1=17，那么5☆3=　　　　 ；当m为实数时，m☆(m☆2)=　　　　　　　　　　　 。

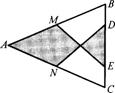13．如图，在△ABC中，AB=AC，M、N分别是AB、AC的中点，D、E为BC上的点，连结DN、EM。若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面积为　　　　　　　  cm²。

14．（本小题满分6分）用换元法解方程：

15．请阅读下列材料：

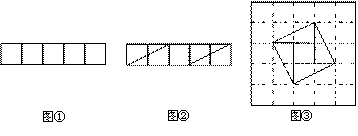
问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形。要求：画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。

小东同学的做法是：设新正方形的边长为x(x＞0)。依题意，割补前后图形的面积相等，有x²=5，解得x=。由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长。于是，画出如图②所示的分割线，拼出如图③所示的新正方形。

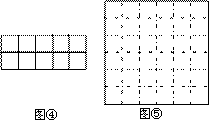
请你参考小东同学的做法，解决如下问题：

现有10个边长为1的正方形，排列形式如图④，请把它们分割后拼接成一个新的正方形。要求：在图④中画出分割线，并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。

16．已知：关于x的方程mx²－14x－7=0有两个实数根x₁和x₂，关于y的方程y²－2(n－1)y＋n²－2n=0有两个实数根y₁和y₂，且－2≤y₁＜y₂≤4。当时，求m的取值范围。

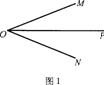
17．如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法，解答下列问题：

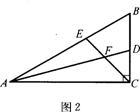
（1）如图②，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系；

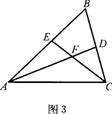
（2）如图③，在△ABC中，如果∠ACB不是直角，而(1)中的其它条件不变，请问，你在(1)中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

18．已知抛物线y=ax²+bx+c与y轴交于点A(0，3)，与x轴分别交于B(1，0)、C(5，0)两点。

（1）求此抛物线的解析式；

（2）若点D为线段OA的一个三等分点，求直线DC的解析式；

（3）若一个动点P自OA的中点M出发，先到达x轴上的某点(设为点E)，再到达抛物线的对称轴上某点(设为点F)，最后运动到点A。求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长。

19．我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形。请解答下列问题：

（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；

（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论。

20．已知：AB是半圆O 的直径，点C在BA的延长线上运动(点C与点A不重合)，以OC为直径的半圆M与半圆O交于点D，∠DCB的平分线与半圆M交于点E。(1)求证：CD是半圆O的切线(图①)；(2)作EF⊥AB于点F(图②)，猜想EF与已有的哪条线段的一半相等，并加以证明；(3)在上述条件下，过点E作CB的平行线CD于点N，当NA与半圆O相切时(图③)，求∠EOC的正切值。

21．已知：抛物线y=－x²+mx+2m²(m＞0)与x轴交于A、B两点，点A在点B的左边，C是抛物线上一个动点(点C与点A、B不重合)，D是OC的中点，连结BD并延长，交AC于点E。

（1）用含m的代数式表示点A、B的坐标；

（2）求的值；

（3）当C、A两点到y轴的距离相等，且时，求抛物线和直线BE的解析式。