初三数学第一学期夜课甲班练习（11） 姓名：____________
1．下列判断中正确的是（ ）
（A）四边相等的四边形是正方形 (B) 四角相等的四边形是正方形
(C) 对角线互相垂直的平行四边形是正方形
(D) 对角线互相垂直平分且相等的四边形是正方形
2．下列图形中，为轴对称图形的是（ ）
3．已知
，则
的值等于（ ）
（A）6
（B）－6 （C）
（D） 
4．若0＜x＜1，则x，x2，x3的大小关系是（ ）
（A）x＜x2＜x3 （B）x＜x3＜x2 （C）x3＜x2＜x （D）x2＜x3＜x
5．如图，在梯形ABCD中，AB//CD，中位线EF与对角线AC、BD交于M、N两点，若EF＝18cm，MN＝8cm，则AB的长等于（
）
（A）10cm （B）13cm（C）20cm （D）26cm
6．若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3，r4，r6，则r3：r4：r6等于（
）
（A）
(B)
(C)
(D) 
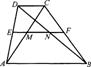
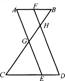
7．如图，AB//CD，AE//FD，AE、FD分别交BC于点G、H，则图中共有相似三角形（ ）
（A）4对 (B) 5对 (C) 6对 (D)7对
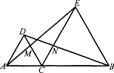8．如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：
① △ACE≌△DCB； ② CM＝CN；③ AC＝DN。其中，正确结论的个数是（ ）
(A) 3个 （B）2个 (C) 1个 （D）0个
9．已知实数a，b，c满足a2＋b2＝1，b2＋c2＝2，c2＋a2＝2，则ab＋bc＋ca的最小值为（ ）
（A）
(B) 
(C) 
(D) 
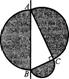10．如图，分别以直角△ABC的三边AB、BC、CA为直径向外作半圆，设直线AB左边阴影部分面积为S1，右边阴影部分面积为S2，则（ ）
A．S1 ＝S2 B．S1 ＜S2 C．S1＞S2 D．无法确定
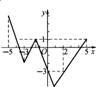11．如图，是某函数的图象，则下列结论正确的是（
）
A．当у＝1时，х的取值是
,5 B．当у＝－3时，х的近似值是0,2
C．当x＝时，函数值у最大 D．当x＝－3时，у随х的增大而增大
12．下列图形是轴对称图形的是
13．根据下表中的规律，从左到右的空格中应依次填写的数字是（
）
|
|
|
|
|
|
|
|
|
| 000 | 110 | 010 | 111 | 001 | 111 |
A．100，011 B．011，100 C．011，101 D．101，110
14．幼儿园小朋友们打算选择一种种形状，大小都相同的多边形塑胶板铺活动室的地面，为了保证铺地时无缝隙又不重叠，请你告诉他们下面形状的塑胶板可以选择的是①三角形②四边形③正五边形④正六边形⑤正八边形（ ）
A．.③④⑤ B．①②④ C．①④ D．①③④⑤
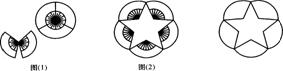
15．下图是由10 把相同的折扇组成的“蝶恋花”（图 l ）和梅花图案（图 2 )（图中的折扇无重叠）, 则梅花图案中的五角星的五个锐角均为（ ）
A . 36º B . 42º C . 45º D . 48º
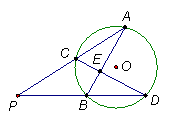
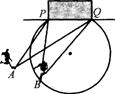16．如图，在世界杯足球比赛中，甲带球向对方球门PQ进攻，当他带球冲到A点时，同伴乙已经助攻冲到B点。有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门，仅从射门角度考虑，应选择 种射门方式。
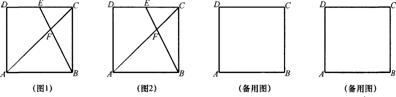
17．将一张纸片沿任何一方翻折,得到折痕AB(如图1);再翻折一次, 得到折痕OC (如图2); 翻折使OA与OC重合, 得到折痕OD(如图3);最后翻折使OB与OC重合, 得到折痕OE(如图4);再恢复到图1形状,则∠DOE的大小是 度
18．北京与纽约的时差为－13(负号表示同一时刻纽约时间与北京时间晚),如果现在是北京时间15:00,那么纽约时间是 .
19．若不等式组
的解集是-1<x<1,则(a+b)2006=
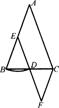
20．在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F.使DF＝DE，连接FC，若∠B＝70°，则∠F＝ 度
21．某圆柱形网球筒，其底部直径是10cm，长为80 cm，将七个这样的网球筒如图所示放置并包装侧面，则需
cm2的包装膜（不计接缝，
取3）
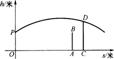22．甲、乙两人进行羽毛球比赛，甲发出一颗十分关键的球，出手点为P，羽毛球飞出的水平距离s（米）与其距地面高度h（米）之间的关系式为
。如图，已知球网AB距原点5米，乙（用线段CD表示）扣球的最大高度为
米，设乙的起跳点C的横坐标为m，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则m的取值范围
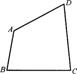23．如图，已四边形纸片ABCD，现需将该纸片剪拼成一个与它面积相等的平行四边形纸片，如果限定裁剪线最多有两条，能否做到：__________（用“能”或“不能”填空）。若填“能”，请确定裁剪线的位置，并说明拼接方法；若填“不能”，请简要说明理由。
____________________________________________________
____________________________________________________
____________________________________________________
24 ．田忌赛马是一个为人熟知的故事．传说战国时期，齐王与田忌各有上、中、下三匹马，同等级的马中，齐王的马比田忌的马强．有一天，齐王要与田忌赛马，双方约定：比赛三局，每局各出一匹，每匹马赛一次，赢得两局者为胜．看样子田忌似乎没有什么胜的希望，但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强 … …
( 1 ）如果齐王将马按上中下的顺序出阵比赛，那么田忌的马如何出阵，田忌才能取胜？ ( 2 ）如果齐王将马按上中下的顺序出阵，而田忌的马随机出阵比赛，田忌获胜的概率是多少？（要求写出双方对阵的所有情况）
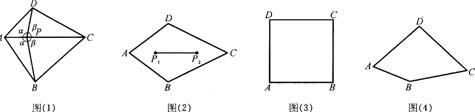
25．如图（ l ) ，凸四边形 ABCD ，如果点P满足∠APD ＝∠APB =α。且∠B P C ＝∠CPD ＝β，则称点P为四边形 ABCD的一个半等角点．
( l ）在图（ 3 ）正方形 ABCD 内画一个半等角点P，且满足α≠β。
( 2 ）在图（ 4 ）四边形 ABCD 中画出一个半等角点P，保留画图痕迹（不需写出画法） .
( 3 ）若四边形 ABCD 有两个半等角点P1 、P2（如图（ 2 ) ) ，证明线段P1 P2上任一点也是它的半等角点 。
26．已知Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8。
（Ⅰ）如图①，若半径为r1的⊙O1是Rt△ABC的内切圆，求r1；
（Ⅱ）如图②，若半径为r2的两个等圆⊙O1、⊙O2外切，且⊙O1与AC、AB相切，⊙O2与BC、AB相切，求r2；
.1230.org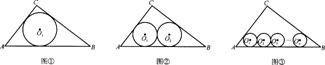
（Ⅲ）如图③，当n大于2的正整数时，若半径rn的n个等圆⊙O1、⊙O2、…、⊙On
依次外切，且⊙O1与AC、BC相切，⊙On与BC、AB相切，⊙O1、⊙O2、⊙O3、…、⊙On－1均与AB边相切，求rn.
27．已知抛物线y＝ax2＋bx＋c的定点坐标为(2,4).
（Ⅰ）试用含a的代数式分别表示b，c；
（Ⅱ）若直线y＝kx＋4（k≠0）与y轴及该抛物线的交点依次为D、E、F，且
，其中O为坐标原点，试用含a的代数式表示k；
（Ⅲ）在（Ⅱ）的条件下，若线段EF的长m满足
，试确定a的取值范围。
28．如图，点E在正方形ABCD的边CD上运动，AC与BE相交于点F（1）如图1，当点E运动到DC的中点时，求△ABF与四边形ADEF的面积之比。
（2）如图2、当点E运动到CE：ED＝2：1时，求△ABF与四边形ADEF的面积之比。
（3）当点E运动到CE：ED＝3：1时，写出△ABF与四边形ADEF的面积之比；当点E运动到CE：ED＝n：1时，（n是正整数）猜想△ABF与四边形ADEF的面积之比（只写结果，不要求写过程）
（4）请你利用上述图形，提出一个类似问题（根据提出的问题给附加分，最多4分，计入总分，但总分不能超过120分）
