初三数学专项复习——视图投影空间几何体

初三数学专项复习——视图投影空间几何体

一、选择题:

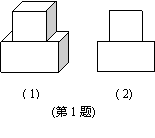1、如图(1)放置的一个机器零件，若其主视图如图(2)，则其俯视图是（　）D

 

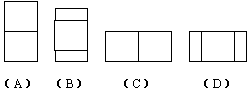
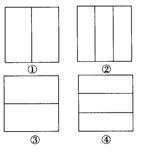2、一物体及其正视图如下图所示，则它的左视图与　 俯视图分别是右侧图形中的（　　）B

(A)①②　　(B)③②

(C)①④　　(D)③④

3、一个几何体的三视图如图所示，那么这个几何　体是（　 ）。C

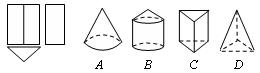
4、如图所示圆柱的左视图是（　　  ）．B

A．　　 　B．　　　　　　 C．　　　　 　D．

5、将如图的Rt△ABC绕直角边AC旋转一周，所得几何体的主视图是（　 ）D

6、如图是小玲在九月初九“重阳节”送给她外婆的礼盒，图中所示礼盒的主视图是（　　）A

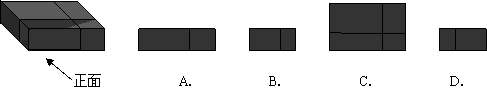7、下面的三个图形是某几何体的三种视图，则该几何体是（　C  ）

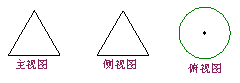A、正方体　 B、圆柱体　　  C、圆锥体　 D、球体

8、下面四个几何体中，主视图、左视图、俯视图是全等图形的几何图形是（　）B

Ａ．圆柱　Ｂ．正方体　 Ｃ．三棱柱　　Ｄ．圆锥

9、一个几何体是由若干个相同的正方体组成的，其主视图和左视图如图所示，则这个几何体最多可由多少个这样的正方体组成？（　　）B

Ａ．12个　　　　　　　 Ｂ．13个　　　　　　

Ｃ．14个　　　　　　　 Ｄ．18个

10、右图表示一个由相同小立方块搭　 成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（　　）C

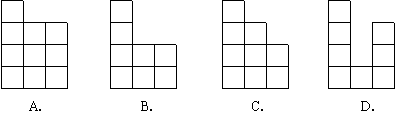11、下图几何体的主视图是（　）C

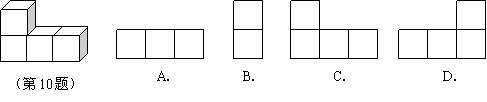
12、如图所示的几何体的右视图（从右边看所得的视图）是　　　　　　　　　　 （　　）A

13、与如图所示的三视图对应的几何体是(　  )B

14、一个几何体的三视图如图所示，这个几何体是（　　）D

Ａ．正方体　　　　　　Ｂ．4

Ｃ．圆锥　　　　 Ｄ．圆柱

15、下列三视图所对应的直观图是（　）C

　A．　　　　　　　　B．　　　　　　 C．　　　　  　　 D．

16、下列四个几何体中，已知某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆，则该几何体是（　　）D

Ａ．球体　　　　　　　Ｂ．长方体　　　　　　　　　Ｃ．圆锥体　　　　　　　　　Ｄ．圆柱体

17、如图，这是一幅电热水壶的主视图，则它的俯视图是（　）D

（第16题图）　　　　　　　　　　A．　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　 D．

18、桌面上放着1个长方体和1个圆柱体，按如图所示的方式摆放在一起，其左视图是（　　）C

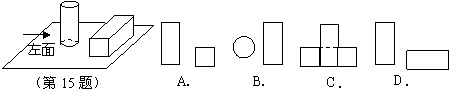
19、小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能是（　　）A

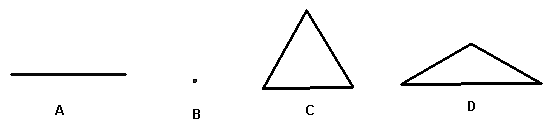20、小明拿一个等边三角形木框在阳光下玩，等边三角形木框在地面上形成的投影不可能是（　　 ）B

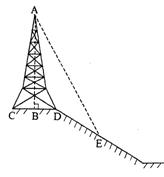21、如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为(　　)A

(A)24m　　(B)22m　　(C)20 m　　(D)18 m

22、如图10，晚上小亮在路灯下散步，在小亮由处走到处这一过程中，他在地上的影子（　　）

Ａ．逐渐变短　　　　　　　　Ｂ．逐渐变长　　　　　　　

Ｃ．先变短后变长　　　　 Ｄ．先变长后变短

二、填空题

1、如果一个立体图形的主视图为矩形，则这个立体图形可能是　　　　　　　  （只需填上一个立体图形）．

答案不唯一如：长方体、圆柱等

2、星期天小川和他爸爸到公园散步，小川身高是160cm，在阳光下他的影长为80cm，爸爸身高180cm，则此时爸爸的影长为＿＿＿＿cm.。　90

3、当太阳光与地面成角时，直立于地面的玲玲测得自己的影长为1.16m，则玲玲的身高约为　　　　 m．（精确到0.01m）　1.66

4、小华在距离路灯6米的地方，发现自己在地面上的影长是2米，如果小华的身高为1.6米，那么路灯离地面的高度是　　　 米.　6.4

5、某同学的身高为1.4米，某一时刻他在阳光下的影长为1.2米，此时，与他相邻的一棵小树的影长为3.6米，则这棵树的高度为　　　　米．4.2

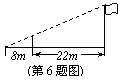6、如图，为了测量学校旗杆的高度，小东用长为3.2的竹竿做测量工具。移动竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为__________m。12

三、解答题

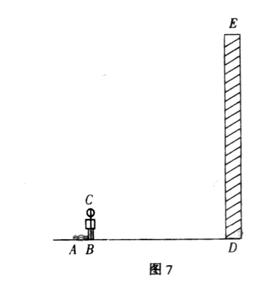
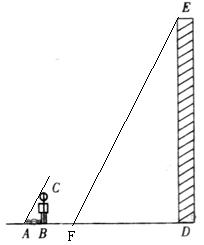1、在一次数学活动课上，李老师带领学生去测教学楼的高度。在阳光下，测得身高1.65米的黄丽同学BC的影厂BA为1.1米，与此同时，测得教学楼DE的影长DF为12.1米。

（1）请你在图7中画出此时教学楼DE在阳光下的投影DF。

（2）请你根据已测得的数据，求出教学楼DE的高度（精确到0.1米）。

解：（1）如左图，注意AC与EF平行；

（2）由，解得：DE＝18.15≈18.2

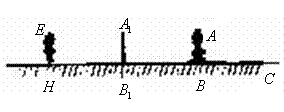
2、学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为的小明的影子长是，而小颖刚好在路灯灯泡的正下方点，并测得．

（1）请在图中画出形成影子的光线，交确定路灯灯泡所在的位置；

（2）求路灯灯泡的垂直高度；

（3）如果小明沿线段向小颖（点）走去，当小明走到中点处时，求其影子的长；当小明继续走剩下路程的到处时，求其影子的长；当小明继续走剩下路程的到处，…按此规律继续走下去，当小明走剩下路程的到处时，其影子的长为　　　　  m（直接用的代数式表示）．

解：（1）

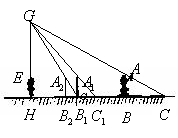
（2）由题意得：，

，，（m）．

（3），，

设长为，则，解得：（m），即（m）．

同理，解得（m），．

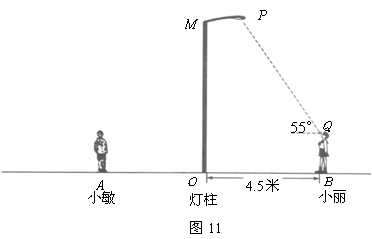
3、（2007广西南宁）如图11所示，点表示广场上的一盏照明灯．

（1）请你在图中画出小敏在照明灯照射下的影子（用线段表示）；

（2）若小丽到灯柱的距离为4.5米，照明灯到灯柱的距离为1.5米，小丽目测照明灯的仰角为，她的目高为1.6米，试求照明灯到地面的距离（结果精确到0.1米）．

（参考数据：，，）

解：（1）如图线段是小敏的影子，

　　（画图正确）

（2）过点作于，

　　过点作于，交于点，

　　则

　　在中，，

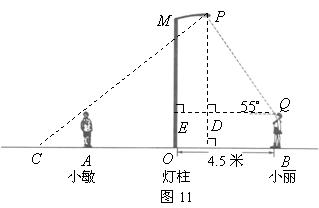
　　　　（米）

　　

　　（米）

　　米

　　（米）

　　答：照明灯到地面的距离为5.9米.

4、如图，某居民小区内两楼之间的距离米，两楼的高都是20米，楼在楼正南，楼窗户朝南．楼内一楼住户的窗台离小区地面的距离米，窗户高米．当正午时刻太阳光线与地面成角时，楼的影子是否影响楼的一楼住户采光？若影响，挡住该住户窗户多高？若不影响，请说明理由．

（参考数据：，，）

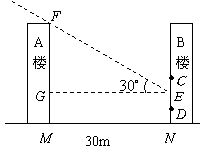解：如图，设光线影响到楼的处，

　　作于，

由题知，，，

　　则，

　　则，

　　因为，所以，

　　即楼影子影响到楼一楼采光，挡住该户窗户米．

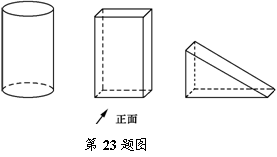
5、如图所给的A、B、C三个几何体中，按箭头所示的方向为它们的正面，设A、B、C三个几何体的主视图分别是A₁、B₁、C₁；左视图分别是A₂、B₂、C₂；俯视图分别是A₃、B₃、C₃．

（1）请你分别写出A₁、A₂、A₃、B₁、B₂、B₃、C₁、C₂、C₃图形的名称；

（2）小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上，并将画有A₁、A₂、A₃的三张卡片放在甲口袋中，画有B₁、B₂、B₃的三张卡片放在乙口袋中，画有C₁、C₂、C₃的三张卡片放在丙口袋中，然后由小亮随机从这三个口袋中分别抽取一张卡片．

① 通过补全下面的树状图，求出小亮随机抽取的三张卡片上的图形名称都相同的概率；

② 小亮和小刚做游戏，游戏规则规定：在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时，小刚获胜；三张卡片上的图形名称完全不同时，小亮获胜．这个游戏对双方公平吗？为什么？

解：（1）　　　　 Ａ　　　　　　Ｂ　　　　　　Ｃ

（2）①树状图：

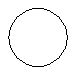
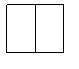
解：（1）由已知可得A₁、A₂是矩形，A₃是圆；B₁、B₂、B₃都是矩形；

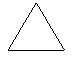
C₁是三角形，C₂、C₃是矩形．　

（2）①补全树状图如下：

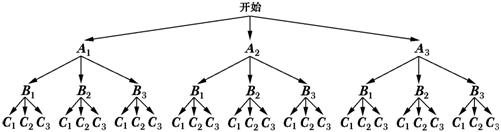
由树状图可知，共有27种等可能结果，其中三张卡片上的图形名称都

相同的结果有12种，∴三张卡片上的图形名称都相同的概率是＝　　

②游戏对双方不公平．由①可知，三张卡片中只有两张卡片上的图形

名称相同的概率是＝，即P_{（小刚获胜）}＝

三张卡片上的图形名称完全不同的概率是＝，即P_{（小亮获胜）}＝

∵＞　∴这个游戏对双方不公平．