初中数学毕业会考考试试卷

初中数学毕业会考考试试卷

数　 学（非课改区：东兴区、资中县）

会考卷（100分）

（考试时间：2006-6-12上午9：00—11：00）

第Ⅰ卷（选择题　共36分）

一、选择题（每小题3分，共计36分）

1、的倒数是(　 )　　

A. -2006　　　 B. 2006　　　 C. 　　　D.

2、台湾是我国最大的岛屿，总面积为35989.76平方千米。用科学记数法应表示为（保留三个有效数字）

A.3.59×10⁶平方千米　　 B.3.60×10⁶平方千米 　C. 3.59×10⁴平方千米　　 D. 3.60×10⁴平方千米

3、一个角的余角比它的补角的少20°，则这个角为(　)

A.30 °　B.40°　　C.60°　　D.75°

4、下列运算正确的是(　 )

 A.a⁵·a³=a¹⁵　　B. a⁵-a³=a² 　　C. (-a⁵)² =a¹⁰ 　　 D. a⁶÷a³=a²

5、在Rt△ABC中，∠C=90°，AB=12，AC=5，则sinA的值是(　　)

A.　　　　  B.　　　　C.　　　　 D.

6、不等式组的解集在数轴上表示正确的是(　　)

7、若一组数据1，2，x，3，4的平均数是3，则这组数据的方差是(　 )

A. 2　　　 B. 　　　C. 10　　　　　　 D.

8、下列方程没有实数根的是(　 )

A. x²-x-1=0　　　　B. x²-6x+5=0　　　 C.　　  D.2x²+x+1=0

9、一辆汽车由内江匀速驶往成都，下列图像中能大致反映汽车距离成都的路程s（千米）和行驶时间t（小时）的关系的是(　 )

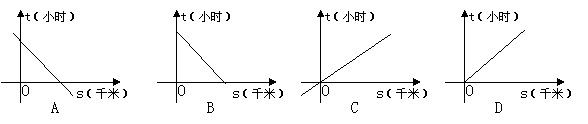10、方程的解是(　 )　

 A.x=1　　 B.x=-4　　 C. x₁=1,x₂=-4　　 D.以上答案都不对

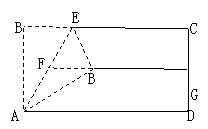
11、如图（1）将矩形纸片ABCD沿AE折叠，使点B落在直角梯形AECD的中位线FG上，若AB=，则AE的长为(　 )

A.　 B. 3　　C. 2　　D.

12、已知⊙O的半径OA=2，弦AB、AC的长分别是、，则∠BAC的度数为(　 )

A.15°　　　B.75°　　 C.15°或75°　　D.15°或45°

第二卷（非选择题　 共64分）

二、填空题（每小题3分，共计12分）

13、函数中，自变量x的取值范围为　　　　　 .

14、方程（x-2）（x-3）=6的解为　　　　　　  .

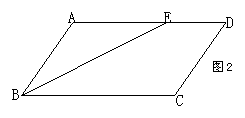
15、如图（2），在中，∠ABC的角平分线BE交AD于E点

AB=5，ED=3，则的周长为　　　　　　　　　  .

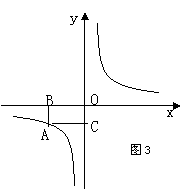
16、如图（3），反比例函数图像上一点A与坐标轴围成的矩形ABOC

的积是8 ，则该反比例函数的解析式为　　　　　　 .

三、解答下列各题（本大题2小题，共计14分）

17、（7分）;

18、（7分）先化简，再求值： ，其中a=，b=1.

四、解答下列各题（本大题2小题，共计15分）

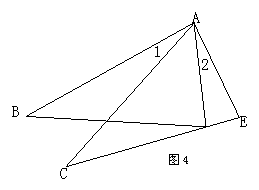
19、（8分）如图（4），在△ABD和△ACE中，有下列四个等式：

1AB=AC 2AD=AE 31=∠24BD=CE.

请你以其中三个等式作为题设，余下的作为结论，

写出一个真命题（要求写出已知，求证及证明过程）

20、（7分）为了了解某校初三年级500名学生的视力情况，

现从中随机抽测了若干名学生的视力作为样本进行数据处理，

并绘出频率分布直方图如下：

已知学生的视力都大于3.95而小于5.40（均为3个有效数字），

图中从左到右五个小长方形的高的比为1：2：3：5：1.视力最好

的一组的频数为5，请你回答以下问题：

(1)共抽测了多少名学生？

(2)若视力不低于4.85属视力正常，低于4.85属视力不正常，

(3)在抽测的学生当中，视力正常的占百分之几？

(4)根据抽样调查结果，清理估算该校初三年级学生当中，

大约有多少名学生视力不正常？

五、解答下列各题（本大题2小题，共15分）

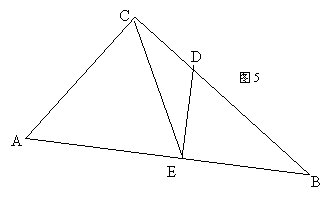21、（7分）如图（5），已知：在Rt△ABC中，∠ACB=90°，sinB=，D是BC上一点，DE⊥AB，垂足为E，CD=DE，AC+CD=9.求：BC的长

22、某学校要印刷一批宣传材料，甲印务公司提出售制版费900元，另外每份材料收印刷费0.5元；乙印务公司提出不受制版费，每份材料收印刷费0.8元。

（1）分别写出两家印务公司的收费y（元）与印刷材料的份数x（份）之间的函数关系式.

（2）若学校预计要印刷5000份以内的宣传材料，请问学校应选择哪一家印务公司更合算？

六、证明题（本大题共8分）

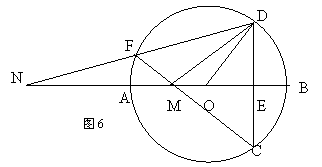23、如图（6）AB是⊙O的直径，弦DC⊥AB于点E，在上取一点F，连结CF交AB于点M，连结DF并延长交BA的延长线于点N.

求证：（1）∠DFC=∠DOB;（2）MN·OM=MC·FM.

加试卷（50分）

一、填空题（本大题5个小题，每小题4分，共20分）

1、已知点P（x-1,x+3）,那么点P不可能在第　　　　象限.

2、某广告公司准备设计衣服形状为梯形的广告牌，要求梯形的四条边长分别为1米、4米、4米、5米，则该广告牌的面积为　　　　　  ___________平方米.

3、若a+2b+3c=12，且a²+b²+c²=ab+bc+ca，则a+b²+c³=　　　　　 .

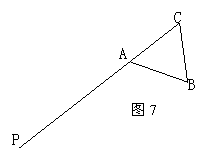
4、如图（7）有一边长为6的正三角形ABC木块（厚度不计），以A为端点，在CA的延长线上拉一条长为15的细绳（细绳的伸缩不计），握住点P拉直细绳，把它全部紧紧缠绕在△ABC木块上（缠绕时木块不动），点P与拉动的路线长为　　　　.

5、对于正数x，规定f（x）= ,

例如f（3）=，f（）=，

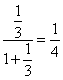计算f（）+ f（）+ f（）+ …f（）+ f（x）+ f（1）+ f（1）+ f（2）+ f（3）+ … + f（2004）+ f（2005）+ f（2006）=　　　　  .

二、解答题（本大题4个小题，共计30分）解答题必须写出必要的文字说明、证明过程或推演步骤.

6、（7分）内江市对城区沿江两岸的部分路段进行亮化工程建设，整个工程拟由甲、乙两个安装公司共同完成。从两个公司的业务资料看到：若两个公司合做，则恰好用12天完成；若甲、乙合做9天后，由甲再单独做5天也恰好完成。如果每天需要支付甲、乙两公司的工程费用分别为1.2万元和0.7万元。

试问：（1）甲、乙两公司单独完成这项工程各需多少天？

（2）要使整个工程费用不超过22.5万元，则乙公司最少应施工多少天？

7、（7分）已知实数x、y、a满足：，试问长度分别为a、y、a的三条线段能否组成一个三角形？如果能，请求出该三角形的面积；如果不能，请说明理由.

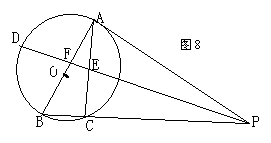8、（8分）如图（8）AB是⊙O的直径，PA切⊙O于点C，∠BPA的角平分线交AC于点E，交AB于点F，交⊙O于点D，∠B=60°，线段BF、AF是一元二次方程的两根（k为常数）

（1）求证：PB·AE=PA·BF.

(2)求证：⊙O的直径是常数k.

（3）求tan∠DPB.

9、（8分）已知，二次函数与x轴交于A、B两点，（A在B的左边），与y轴交于点C，且∠ACB=90°.

(1)求这个二次函数的解析式.

(2)矩形DEFG的一条边DG在AB上，E、F分别在BC、AC上，设OD=x，矩形DEFG的面积为S，求S关于x的函数解析式.

（3）将（1）中所得抛物线向左平移2个单位后，与x轴交于，矩形的一条边在上 ，分别在抛物线上，矩形的周长是否存在最大值，若存在，请求出最大值；若不存在，请说明理由.