| 座位号 |
初中数学毕业诊断考试试卷
数 学
| 题号 | 一 | 二 | 三 | 总分 |
| 得分 |
本试卷满分150分,考试用时120分钟。
| 得分 | 评卷人 |
一、选择题(本大题共12个小题,每小题4分,共计48分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1、点A(2,-3)关于x轴的对称点的坐标为 ( )
(A) (2,3) (B) (-2,-3)(C) (-2,3)(D) (2,-3)
2、如果反比例函数![]() 的图象经过点(-2,3),那么
的图象经过点(-2,3),那么![]() 的值是
(
)
的值是
(
)
(A) ![]() (B)
(B) ![]() (C)
6 (D) -6
(C)
6 (D) -6
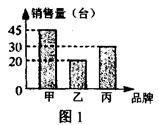
3、如图1是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售之和为 ( )
(A) 50台 (B) 65台 (C) 75台 (D) 95台
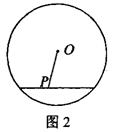
4、如图2,⊙O的直径为10,弦AB的长为6,P为弦AB上的动点,则OP的长的取值范围是 ( )
(A) 4≤OP≤5 (B) 3≤OP≤5 (C) 4<OP<5 (D) 3<OP<5
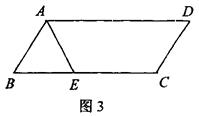
5、如图3,在平行四边形ABCD中,AD=5,AB=2,AE平分∠BAD交BC于E,则线段BE、EC的长分别为 ( )
(A)3和2 (B) 2和3 (C) 4和1 (D) 1和4
6、已知⊙O1与⊙O2的半径长分别是方程![]() 的两根,且O1O2=
的两根,且O1O2=![]() ,则⊙O1与⊙O2的位置关系是
( )
,则⊙O1与⊙O2的位置关系是
( )
(A) 相交 (B) 内切 (C) 内含 (D) 外切
7、矩形分别按以下虚线剪开能拼成三角形、梯形,又能拼成平行四边形的是 ( )
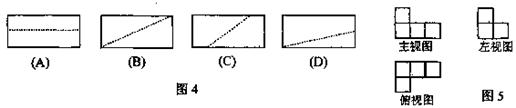
8、由一些大小相同的小正方形组成的几何体的三视图如图5所示,那么,组成这个几何体的小正方体有 ( )
(A)6块 (B)5块 (C)4块 (D)3块
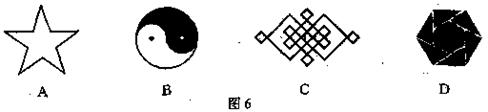
9、下面给出的是产品的图案,从几何图形的角度看,这些图案既是中心对称图形又是轴
对称图形的是 ( )
10、把一个正方形的一边增加
(A)1 (B)2 (C)3 (D)6
11、将抛物线![]() 绕原点按顺时针方向旋转180°后,再分别向下、向右平移1个单位,此时该抛物线的解析式为 ( )
绕原点按顺时针方向旋转180°后,再分别向下、向右平移1个单位,此时该抛物线的解析式为 ( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
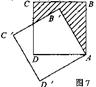
12、如图7,边长为a的正方形ABCD绕点A逆时针方向旋转30°得到正方形AB′C′D′,图中阴影部分的面积为 ( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
| 得分 | 评卷人 |
二、填空题(本大题共8个小题,每小题4分,共计32分)
13、函数![]() 中自变量的取值范围是
,函数
中自变量的取值范围是
,函数![]() 中,自变量
中,自变量![]() 的取值范围是
。
的取值范围是
。
14、在5张卡片上分别写有实数![]() ,
,![]() ,
,![]() ,3.14,
,3.14,![]() ,从中随机抽取一张卡片,抽到无理数的概率是
。
,从中随机抽取一张卡片,抽到无理数的概率是
。
15、如图8,粮仓的顶部是一圆锥形,这个圆锥底面半径为![]() m,母线长为
m,母线长为
 16、如图9,已知两点A(2,0),B(0,4),且
16、如图9,已知两点A(2,0),B(0,4),且![]() ,则点C的坐标为 。
,则点C的坐标为 。
17、四个容量相等的容器形状如图1,以同一流量的水管分别注水到这四个容器,所需时间都相同,图2的图象显示注水时,容器水位(h)与时间(t)的关系,请分别把图象序号与相应容器形状的字母代号用线段相连接: 。
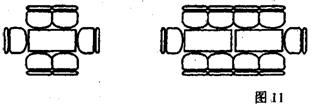
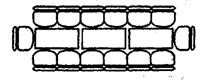
18、某学校图书馆阅览室按下列方式(图11)摆放桌子和椅子,当摆放儿n+1张桌子时,椅子应摆放 张。
 19、已知二次函数
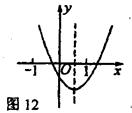
19、已知二次函数![]() 的图象如图12所示,以下关于a,b,c的不等式中正确的序号是
。
的图象如图12所示,以下关于a,b,c的不等式中正确的序号是
。
①![]() ②
②![]() ③
③![]() ④
④![]()
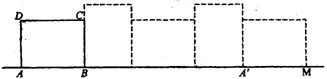
20、已知矩形ABCD的长AB=8,宽AD=6,按如图13放置在直线AM上,然后不滑动地转动,当它转动一周时(A→A′),顶点A所经过的路线长等于 。
| 得分 | 评卷人 |
三、计算题(本大题共10个小题,共计70分)
21、(5分)计算:![]()
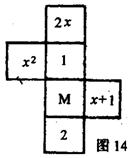
22、(6分)如图14是一个正方形的展开图,标注了字母M的面是正方体的正面,如果正方体的左面与右面所标注的代数式的值相等,求x的值。
23、(6分)方程![]() 与二元一次方程组
与二元一次方程组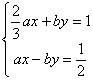 有相同的解,且
有相同的解,且![]() ,求锐角
,求锐角![]() 的大小。
的大小。
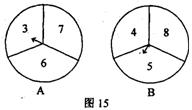
24.(6分)如图15,由转盘和箭头组成的两个装置,装置A、B的转盘分别被分成三个面积相等的扇形,装置A上的数字分别是3,6,7,装置B上的数字分别是4,5,8,这两个装置除了表面数字不同外,其他构造完全相同,现在你和另外一个人分别同时同力转动A、B两个转盘中的箭头,如果我们规定箭头停留在较大数字的一方获胜(若箭头恰好停留在分解线上,则重新转动一次,直到箭头停留在某一数字为止),那么你会选择哪个装置呢?请借助列表法或树状图法说明理由。
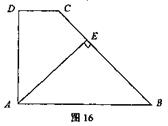
25、(7分)如图16,已知:在直角梯形ABCD中,AB∥CD, AD⊥CD,AB=BC,又AE⊥BC于
E。求证:AD=AE.
26、(7分)已知反比例函数![]() 的图象经过点M(4,
的图象经过点M(4,![]() ),若函数
),若函数![]() 的图象平移后经过反比例函数图象上一点A(2,m),求平移后的函数图象与反比例函数
的图象平移后经过反比例函数图象上一点A(2,m),求平移后的函数图象与反比例函数![]() 图象的另一个交点B的坐标。
图象的另一个交点B的坐标。
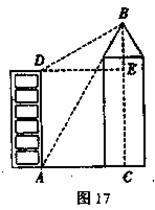
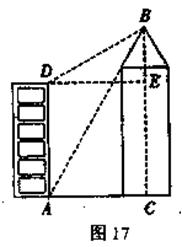
27、(8分)小强的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小强想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离.于时小强在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°,已知公寓楼AD的高为
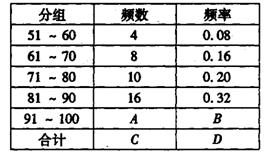
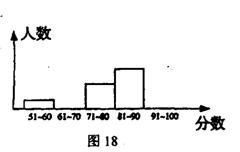
28、(8分)为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加,为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取整数,满分100分)进行统讨。请你根据下面尚未完成的图表和频数分布直方图(如图18),解答下列问题:
(1)求出表中A、B、C、D的值;
(2)补全频数分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)
(4)若成绩在90分(不含90分)以上为优秀,则该校成绩优秀的约为多少人?
29、(8分)如图19,AB是⊙o的直径,BC是⊙o 的切线,D是⊙o 上的一点,且AD∥OC,
(1)求证△ADB∽△OBC; .
(2)若AO=2,BC=2![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)

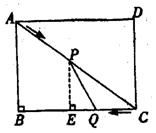
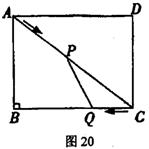
30、(9分)如图20,在矩形ABCD中,AB=
沿AC向点C移动,同时动点Q为lm/s的速度从点C出发,沿CB向点B移动,设P、Q两点分别移动ts(0<t<5)后,P点到BC的距离为dm,四边形ABQP的面积为S㎡
(1)求距离d关于时间t的函数关系式;
(2)求面积S关于时间t的函数关系式;
(3>在P、Q两点移动的过程中,四边形ABQP的面积能否是△CPQ面积的3倍?若能,求出此时点P的位置;若不能,请说明理由.
2007年初中毕业诊断考试试题
数学参考答案及评分标准
一、选择题(本大题共12个小题,每小题4分,共计48分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1、A 2、D 3、C 4、A 5、B 6、A 7、D 8、B 9、C 10、D 11、A 12、C
二、填空题(本大题共8个小题,每小题4分,共计32分)
13、![]()
![]() 14、
14、![]() 15、90 16、(0,1)
15、90 16、(0,1)
17、A—(3) B—(4) C --(2) D—(1) 18、![]() 19、
①②③ 20、
19、
①②③ 20、![]()
三、计算题(本大题共10个小题,共计70分)
21、解:原式=![]() ……………………4分
……………………4分
=![]() ……………………5分
……………………5分
22、解:由图可知:![]() 即
即 ![]() ……………………2分
……………………2分
∵ ![]() ……………………4分
……………………4分
∴![]()
![]()
∴![]() 的值为
的值为![]() 或
或![]() ……………………6分
……………………6分
23、解:方程![]() 的解为
的解为![]() ……………………2分
……………………2分
由题意得,此解也是方程组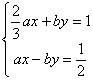 的解,
的解,
故有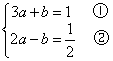 ……………………4分
……………………4分
①-②得![]() ……………………5分
……………………5分
由已知![]() ,且
,且![]() 为锐角,所以
为锐角,所以![]() =30°
……………………6分
=30°
……………………6分
24、解:列表:
|
| 4 | 5 | 6 |
| 3 | (3,4) | (3,5) | (3,8) |
| 6 | (6,4) | (6,5) | (6,8) |
| 7 | (7,4) | (7,5) | (7,8) |
……………2分
∴P(A)=![]() P(B)=
P(B)=![]() ……………4 分
……………4 分
∵P(A)< P(B) ,所以选择B ……………6 分
25、证明:连结AC
∵AB=BC
∴∠BAC=∠BCA ……………2分
又∵AB∥CD
∴∠BAC=∠ACD
∴∠ACD=∠ACE ……………4分
∵∠ADC=∠AEC=90°
又AC=AC
∴△ACD≌△ACE ……………6分
∴AD=AE ……………7分
26、解:∵点M(4,![]() )在反比例函数
)在反比例函数![]() 的图像上,
的图像上,
∴![]() ,故反比例函数解析式为
,故反比例函数解析式为![]() ……………2分
……………2分
又点A(2,m)在反比例函数的图像上
∴m=1,故点A坐标为(2,1) ……………4分
设y=x图象平移后的解析式为y=x+b又已知y=x+b的图象过点A(2,1)
∴1=2+b ∴ b=-1
故得y=x图象平移后所得图象的函数解析式为一次函数![]() ……6分
……6分
由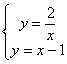 解得另一交点为(-1,-2)
……………7分
解得另一交点为(-1,-2)
……………7分
27、解:如图,由题意知:四边形ACED是矩形,
∴AC=DE,DA=EC=
设DE=![]() ,在Rt△BDE中,∵
,在Rt△BDE中,∵![]() ∠BDE=
∠BDE=![]()
∴BE=![]() …………4分
…………4分
在Rt△BAC中,∵![]() ,即
,即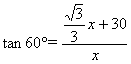
∴![]() ,解得
,解得![]() …………6分
…………6分
∴![]() …………8分
…………8分
28、解:(1)A=12 B=
(2)如图:
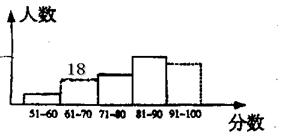
(3)成绩落在81—90分数段内的学生最多. ……(6分)
(4)该校成绩优秀的约为:0.24×900=216(人) ……(8分)
29、证明:(1)∵AB是⊙O的直径 ∴∠ADB=90°
∵BC是⊙O的切线,OB为半径, ∴∠OBC=90°
又∵AD∥OC,∴∠A=∠COB ……(2分)
∴在Rt △ADB和△OBC中∠ADB=∠OBC=90。,∠A=∠COB
∴△ADB∽△OBC ……(4分)
(2)由(1)得![]() ,即=
,即=![]()
∵AO=2,BC=2![]() ,OC=
,OC=![]() ……(6分)
……(6分)
∴![]() ……(8分)
……(8分)
30.解:(1)过点P作PE⊥BC于E,Rt△ABC中,AC=![]() (m)
(m)
由题意知:AP=2t,CQ=t,则PC=10—2t. ……(1分)
由AB⊥BC,PE⊥BC,得PE∥AB,
∴![]() ,即
,即![]() …………(2分)
…………(2分)
∴![]()
即![]() …··(3分)
…··(3分)
(2)∵![]() ……(4分)
……(4分)
∴S=![]()
![]() =
=![]() 即
即![]() ……(6分)
……(6分)
(3)假设四边形ABQP的面积是△CPQ面积的3倍,则有:![]() ,
,
即![]() ..。..(7分)
..。..(7分)
∵![]() ,方程无解,
… ……(8分)
,方程无解,
… ……(8分)
∴在P,Q两点移动的过程中,四边形ABQP的面积不可能是△CPQ面积的3倍……(9分)