高中提前招生数学模拟题
一、选择题（本题有12小题，每小题3分，共36分，请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
1.下列计算正确的是（ ）
A、2
·
B、
C、
D、（
2．抛物线
的顶点坐标是 （ ）
A、（2，8） B、（8，2） C、（—8，2） D、（—8，—2）
3．已知圆锥的底面半径为9㎝，母线长为30㎝，则圆锥的侧面积为（ ）
A、270π
B、360π C、450π D、540π
4．如图，已知AB∥CD，AB=CD,AE=FD,则图中的全等三角形有 （ ）
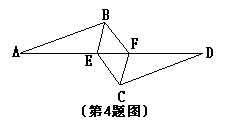A、1对
B、2对
C、3对
D、4对
5．现有2008年奥运会福娃卡片20张，其
中贝贝6张，京京5张，欢欢4张，迎迎3张，
妮妮2张，每张卡片大小、质地均匀相同，将
画有福娃的一面朝下反扣在桌子上，从中随机
抽取一张，抽到京京的概率是 （ ）
A、
B、
C、
D、
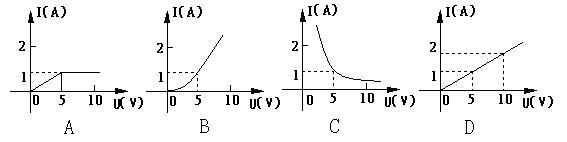
6．如果一个定值电阻R两端所加电压为5伏时，通过它的电流为1安培，那么通过这一电阻的电流I随它的两端电压U变化的图像是 （ ）
7．如图是5×5的正方形网络，以点D、E为两个顶点作位
置不同的格点三角形，使所作的格点三角形与△ABC全等，
这样的格点三角形最多可以画出 （ ）
A、2个 B、4个 C、6个 D、8个
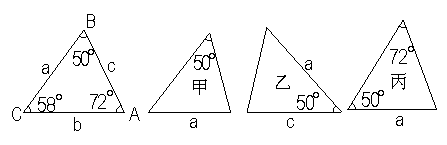8.如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是（ ）
A、甲乙 B、甲丙 C、乙丙 D、乙
9．如图，∠ACB＝60○，半径为2的⊙0切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为 （ ）
A、2π
B、4π C、
D、4
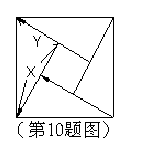
10．如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用X、Y表示直角三角形的两直角边（x＞y），请观察图案，指出以下关系式中不正确的是 （ ）
A、x2＋y2＝49 B、x－y＝2 C、2xy＋4＝49 D、x＋yY＝13
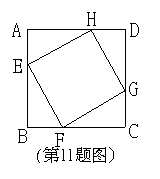
11．如图，正方形ABCD边长为1，E、F、G、H分别为各边上的点，且AE=BF=CG=DH,设小正方形EFGH的面积为Y，AE为X，则Y关于X的函数图象大致是 （ ）
12．先作半径为
的圆的内接正方形，接着作上述内接正方形的内切圆，再作上述内切圆的内接正方形，…，则按以上规律作出的第7个圆的内接正方形的边长为 （ ）
A、（
B、（
C、（
D、
二、填空题（第小题4分，共24分）
13．我们知道，1纳米=10—9米，一种花粉直径为35000纳米，那么这种花粉的直径用科学记数法可记为 米。
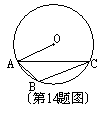
14．如图，A、B、C为⊙0上三点，∠ACB＝200,
则∠BAO的度数为 0。
15. 如图，△ABC的外接圆的圆心坐标为 。
16．如图，用同样规格的黑白两色的正方形瓷砖铺设矩形地面，
请观察图形并解答下列问题。
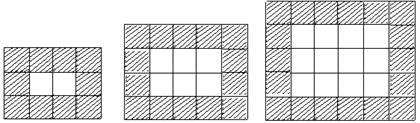
n=1
n=2
n=3
在第n个图中，共有 白块瓷砖。
（用含n的代数式表示）
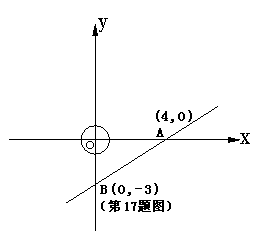
17．直角坐标系中直线AB交x轴，y轴于点A（4，0）
与 B（0，-3），现有一半径为1的动圆的圆心位
于原点处，以每秒1个单位的速度向右作平移运动，
则经过 秒后动圆与直线AB相切。
18．小明设计了一个电子游戏：一电子跳蚤从横坐
标为t(t＞0)的P1点开始，按点的横坐标依次
增加1的规律，在抛物线
＞0)上向
右跳动，得到点P2、P3，这时△P1P2P3的面积为 。
三．解答题（第19题第小题5分，第20题8分，
第21、22、23题各为10分，第24题12分）
19.（1）计算
（2）化简
| 降价次数 | 一 | 二 | 三 |
| 销售件数 | 10 | 40 | 一抢而光 |
20.本商店积压了100件某种商品，为使这批货物尽快出售，该商店采取了如下销售方案，先将价格提高到原来的2.5倍，再作三次降价处理；第一次降价30%标出了“亏本价”，第二次降价30%，标出“破产价”，第三次又降价30%,标出“跳楼价”，三次降价处理销售情况如右表。
问：（1）跳楼价占原价的百分比是多少？
（2）该商品按新销售方案销售，相比原价全部售完，哪一种方案更盈利，请通过计算加以说明.
21.如图，在5×5的正方形网格中，每个小正方形的边长都为1，
请在所给网格中按下列要求画出图形。
（1）从点A出发的一条线段AB，使它的另一个端点
落在格点（即小正方形的顶点）上，且长度为
；
（2）以（1）中的AB为边的一个等腰三角形ABC，
使点C在格点上，且另两边的长都是无理数；
（3）以（1）中的AB为边的两个凸多边形，使它
们都是中心对称图形且不全等，其顶点都在格点上，各边长都是无理数。
22.如图，正方形ABCD和正方形EFGH的边长分别为
，对角线BD、FH都在直线L上，O1、O2分别是正方形的中心，线段O1O2的长叫做两个正方形的中心距。当中心O2在直线L上平移时，正方形EFGH也随平移，在平移时正方形EFGH的形状、大小没有改变。
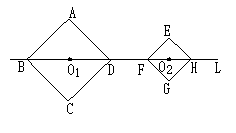（1）计算：O1D= ，O2F= 。
（2）当中心O2在直线L上平移到两个正方
形只有一个公共点时，中心距O1O2= 。
（3）随着中心O2在直线L上的平移，两个正方形的公共
点的个数还有哪些变化？并求出相对应的中心距的值或取 （第22题图）
值范围（不必写出计算过程）。
23．据某气象中心观察和预测：发生于M地的沙尘暴一直向正南方向移动，其移动速度V（km/h）与时间t（h）的函数图象如图所示，过线段OC上一点T（t,O）作横轴的垂线L，梯形OABC在直线L左侧部分的面积即为t（h）内沙尘暴所经过的路程S（km）.
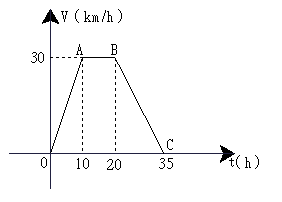(1)当t=4时，求S的值；
（2）将S随t变化的规律用数学关系式表示出来；
（3）若N城位于M地正南方向，且距M地
650km，试判断这场沙尘暴是否会侵袭到N
城，如果会，在沙尘暴发生后多长时间它将
侵袭到N城？如果不会，请说明理由。
24.如图，点A在Y轴上，点B在X轴上，且OA=OB=1，经过原点O的直线L交线段AB于点C，过C作OC的垂线，与直线X=1相交于点P，现将直线L绕O点旋转，使交点C从A向B运动，但C点必须在第一象限内，并记AC的长为t，分析此图后，对下列问题作出探究：
（1）当△AOC和△BCP全等时，求出t的值。
（2）通过动手测量线段OC和CP的长来判断它们之间的大小关系？并证明你得到的结论。
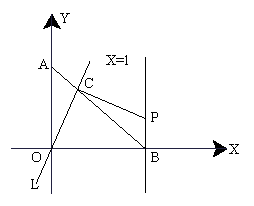（3）①设点P的坐标为（1,b）,试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
参考答案
一．选择题
DBACC DBCCD BA
二、填空题
13.3.5×10-5 14.70○ 15.（6.2） 16.n(n＋1) 17.
18.1
三、解答题
19.（1）原式=8＋1＋9（3分） （2）原式=
（2分）
=18 （5分）
=
（3分）
=
（5分）
20.设原价为1
（1）亏本价=1×2.5（1－30%）=1.75 （1分）
破产价=1.75（1－30%）=1.225 （2分）
跳楼价=1.225（1－30%）=0.8575
跳楼价占原价的百分比为85.75% （4分）
（2）原价销售额：100×1=100 （5分）
实际销售额：10×1.75＋40×1.225＋50×0.8575=109.375（7分）
∴按新销售方案销售更盈利。 （8分）
21.（1）AB为所作线段 （3分）
（2）△ABC或△ABC2都可 （6分）
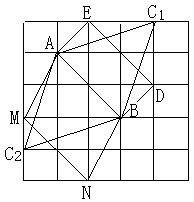（3）ABDE或者四边形ABNM等 （10分）
22.（1）O1D=2 O2F=1 （3分）
（2）O1O2=3 （5分）
（3）两个公共点 1＜O1O2＜3 （6分）
无数个公共点 O1O2=1 （7分）
1个公共点 O1O2=3 （8分）
无公共点 O1O2＞3或0≤O1O2＜1（10分）
23.（1）UOA=3t
S=
(3分)
（2）S1=
（0≤t≤10）
S2=30t－150 (10＜t≤20）
S3=-t2＋70t－550（20＜t≤35） （7分）
（3）S1=
≤t≤10)最大值为150≤650
S2=30t－150=650 ∴t=
＞20不可能
S3=－
∴t1=30，t2=40，∵20＜t≤35 ∴t=30 （10分）
24．（1）t=
（3分）
（2）OC=CP （4分）
过点C作X轴的平行线，交OA与直线BP于点T、H，
证△OTC≌△CHP即可 （7分）
（3）①
（0≤t≤1）
（10分）
②当t=0或1时，△PBC为等腰三角形，
即P（1.1）, P（1，1－
） （12分 ）