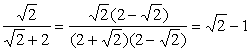中考数学总复习专题训练（二)粤教

中考数学总复习专题训练（二)　

 （代数式）

考试时间：120分钟 满分150分

一、选择题（每小题3分，共45分）

1.下列式子中，符合代数式的书写格式的是（　 ）。

A.　　　 B.3x²y　　　　C.a÷2b　　　 D.x+y小时

2、下列运算中，结果正确的是（　 ）。

A．　　　　　　 B．

C．　　　　　　 D．

3、计算 a^m÷aⁿ÷a^p 等于（　 ）。

　　A． a^m-n-p　　　 B. a^m+n-p　 　　 C.　a^m-n+p D.  a^m+n+p　　　

4、计算 (－2a²)²的结果是（　 ）。

A. 2a⁴ 　　　　B. －2a⁴　　　　C. 4a⁴ 　　　　 D．－4a⁴

5、下列式子中，正确的是（　 ）。　　　　　　　　　　　　　　　　　　  　 

　　A.　( - a² b )²·a = a⁵ b²　　　　　B. ( - b⁸ )· ( - b )²　= b¹⁰　

　　C．〔 ( -1

) a⁴〕²= - a⁸　　　　 　D. ( - a³ b c² )²　=  a⁶ b c⁴　　

6、使式子有意义的x取值范围为（　 ）。

A.x>0　　　　　  B.x≠1　　　　 C.x≠-1　　　　D．x≠±1

7．等式＝成立的条件是（　 ）。

A.－2<x≤3　 　　B.－2≤x≤3　 　C.x>－2　 　　 D．x≤3

8．把分式中的x,y都扩大两倍,那么分式的值（　 ）。

A.扩大两倍　　　　B. 不变　 　　　C. 缩小　　　　D． 缩小两倍

9．在二次根式， ， ， ， 中，最简二次根式个数是（　 ）。

A.1个　　　　  　B.2个 　　　　　 C.3个 　　　　D．4个

10．当1<x<2时，化简∣1－x∣＋的结果是（　 ）。

A.－1　　　　　　 B.2x－1　　　　　 C.1　 　　　　D．3－2x

11．＋()²的值一定是（　 ）。

A.0　 　　　　　　B.4－2x　　　　　 C.2x－4 　　　D．4

12、已知下列四个根式:①②③④，其中是同类二次根式的有（　 ）。

A.①②③　　　　　 B.①②④　　　　  C.①③④　　 D．②③④

13、 化简的结果是（　 ）。

A.　 　　　　　 B. 　　　　  C.2x　　　D．

14、设P是关于x的五次多项式，Q是关于x的三次多项式，则（　 ）。

A.P+Q是关于的八次多项式　　　B.P-Q是关于的二次多项式

C.P·Q是关于的八次多项式　　 D．是关于的二次多项式

15．不论ａ为何值，代数式－ａ²＋4ａ－5值（　 ）。

A.大于或等于0　　　　B.0　　　　　　 C.大于0　　　D．小于0

二、填空题（每小题3分，共45分）

1、－的系数是_________，是_________次单项式。

2、分解因式2x²-4xy +2y²=__________________。

3、分解因式: ab－a+b－1=_________________________________。

4、计算的结果是______________。

5、若x²+kx－6有一个因式是(x－2)，则k的值是_________。

6、比较大小：_________．（填“”、“”或“”）

7、通过计算可知：，，，则下一个类似的式子是_________。　　

8、单项式与是同类项，则的值为_________。

9、一个十位数字是a，个位数字是b的两位数表示为10a＋b，交换这个两位数的十位数字和个位数字，又得一个新的两位数，它是_________，这两个数的差是_________。

10．代数式y²＋my＋是一个完全平方式，则m的值是_________。

11．(x²＋y²)(x²－1＋y²)－12＝0,则x²＋y²的值是_________。

12.已知2a－b＝4,　2(b－2a)²－3(b－2a)＋1＝_________。

13、一张纸片，第一次把它撕成3片， 第二次把其中一片又撕成3片，…如此下去，第n次撕后共得小纸片_________片。

14、某音像公司对外出租光盘的收费标准是：每张光盘出租后的前3天每天收费0.5元，以后每天收费0.3元，那么一张光盘在出租后第n天（n＞3且为整数）应收费_________元。

15、将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_________条折痕,如果对折n次,可以得到_________条折痕。

三、解答下列各题（每小题6分，共 60 分）

1、先化简，再求值：，其中。

2、如图，化简x－y+1－2y－x－3+y－x+5。

3、若3，ｍ，5为三角形三边，化简：－。

4、邮购一种图书，每本定价m元，不足100本时，每本书要加书价的10℅作为邮资。

（1）要邮购x（x＜100的正整数）本，总计金额是多少元？

（2）当一次购书超过100本时，书店除免付邮资外，还给予10℅的优惠。计算当m=3元时，邮购本数x为120时的总计金额是多少元？

5、在现实生活中有两种表示温度的方法：摄氏（C）和华氏(F)，它们之间有如下的关系：  C=（F-32）。

⑴请问，一个人的体温可以达到100℉吗？

⑵某一天早晨我国上海的气温是12℃，澳大利亚的气温是59℉，你能知道这天早晨哪个地方的气温高吗？高多少摄氏度？

6、求多项式：10X³-6X²+5X-4与多项式-9X³+2X²+4X-2的差。

7、化简(–　)÷。

8、已知代数式3ｙ²－2ｙ＋6的值为8，求代数式ｙ²－ｙ＋1的值。

9、＝求的值。

10、化简求值: , 其中x=。

参考答案

一、1、A　2、C　3、A　4、C　5、A　 6、D　7、A　8、B　9、B　10、 C　

　11、B　 12、C　 13、B　 14、C　 15、D

二、1、，5； 2、； 3、(a+1)(b－1)； 4、； 5、1； 6、； 7、　； 8、4； 9、10b＋a, 9a-9b； 10、±5； 11、4； 12、45； 13、2n+1； 14、0.3n+0.6； 15、15，。

三、1、原式=,当时，原式=-8；　2、0； 3、2 m-10；

4、(1)(1+10℅)mx，(2)（1-10℅）mx，当m=3，x=120时，（1-10℅）mx=（1-10℅）×3×120=324（元）。

5、⑴当F=100时，C=（F-32）=（100-32）≈37.8℃ 所以，一个人的体温可以达到100℉。

(2)当F=59时，C=（F-32）=（59-32）=15℃，

因为12℃＞15℃，所以，澳大利亚的气温高，高3℃。

6、；7、；8、2；

9、由已知得，则，所以原式=；

10、原式==

==

当x=时, 原式=