中考数学总复习专题训练（十三)
（中考模拟一）
考试时间：120分钟 满分150分
一、选择题（本题共10小题，每小题4分，满分40分）
每一个小题都给出代号为Ａ，Ｂ，Ｃ，Ｄ的四个结论，其中只有一个是正确的，把正确结论的代号写在题后的括号内．每一小题：选对得4分，不选、选错或选出的代号超过一个的（不论是否写在括号内）均不得分。
1．已知点P（3，－2）与点Q关于x轴对称，则Q点的坐标为（ ）
A．（－3，2） B.（－3，－2） C.（3，2） D.（3，－2）
2．如图（1），在等腰直角△ABC中，
B＝90°，将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′则
等于（ ）
A． 60° B. 105° C.120° D. 135°
3．下列四个函数中，y随x增大而减小的是( )
A．y=2x B．y=―2x+5 C．y=―
D．y=―x2+2x―1
4．据“保护长江万里行”考察队统计，仅2003年长江流域废水排放量已达163.9亿吨！治长江污染真是刻不容缓了！请将这个数据用四舍五入法，使其保留两个有效数字，再用科学记数法表示出来是（ ）
A．
亿吨 B.
亿吨 C.
亿吨 D.
亿吨
5．直线
经过第二、三、四象限那么下列结论正确的是（ ）
A．
B.点（a，b）在第一象限内
C.反比例函数
当
时函数值
随
增大而减小
D.抛物线
的对称轴过二、三象限
6、如图（2），CD是
斜边AB上的高，将
BCD沿CD折叠，B点恰好落在AB的中点E处，则A等于（ ）
A．25
B．30
C．45
D．60
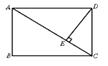
7．如图（3），在矩形ABCD中，DE⊥AC于E，设∠ADE＝α，且cosα＝
，AB＝4，则AD的长为( )
A．3 B．
C．
D．
图（2） 图（3）
8．如图（4）所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a，较短直角边为b，则a3＋b4的值为( )
A．35 B．43 C．89 D．97
9．一位美术老师在课堂上进行立体模型素描教学时，把14个棱长为 1 分米的正方体摆在课桌上成如图5形式，然后他把露出的表面都涂上不同的颜色，则被他涂上颜色部分的面积为( )
A． 33分米2
B．24分米2
C．21分米2 D．42分米2
图（4） 图（5）
10．已知：关于x的一元二次方程x2-(R＋r)x＋
d2＝0无实数根，其 中R、r分别是⊙O1、⊙O2的半径，d为此两圆的圆心距，则⊙O1，⊙O2的位置关系为( )
A．外离 B．相切 C．相交 D．内含
二、填空题（本题共4小题，每小题5分，满分20分）
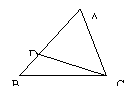
11、如图（6），请你补充一个你认为正确的条件，使
∽
：______
。
12、写出一个解为
的二元一次方程组______
。
13．如图（7），两建筑物AB和CD的水平距离为30米，从A点测得D点的俯角为30°，测得C点的俯角为60°，则建筑物CD的高为
米。
图（6）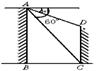 
图（7）
14．先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB、AD分别落在x轴、y轴上(如图8)，再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图9)，若AB＝4，BC＝3，则图8和图9中B点的坐标为 点C的坐标 。
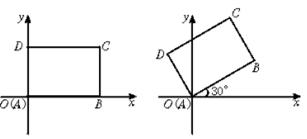
图（8） 图（9）
三、（本题共2小题，每小题8分，满分16分）
15．
计算： 
－sin60°＋（－
）0－
。
16．如图10，一次函数
的图象与反比例函数
图象交于
A（－2，1）、B（1，n）两点。
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。
 |
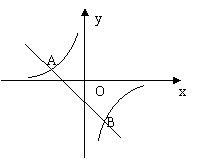四、（本题共2小题，每小题8分，满分16分）
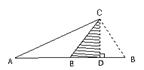
17．如图11（单位：m），等腰三角形ABC以2米/秒的速度沿直线L向正方形移动，直到AB与CD重合。设x秒时，三角形与正方形重叠部分的面积为y
。
（1）写出y与x的关系式；
（2）当x＝2，3.5时，y分别是多少？
（3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？
 |
18、下表是某居民小区五月份的用水情况：
| 月用水量(米3) | 4 | 5 | 6 | 8 | 9 | 11 |
| 户数 | 2 | 3 | 7 | 5 | 2 | 1 |
(1)计算20户家庭的月平均用水量；
(2)画出这20户家庭月用水量的频数分布直方图；
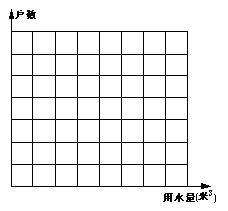(3)如果该小区有500户家庭，根据上面的计算结果，
估计该小区居民每月共用水多少立方米?
五、（本题共2小题，每小题10分，满分20分）
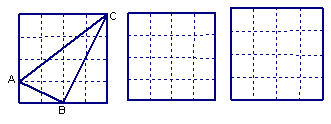19．正方形网格中，小格的顶点叫做格点。小华按下列要求作图：①在正方
形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等。
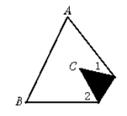20．如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，求∠2的度数。
六、（本题满分12分）
21、如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直经BD=6，连结CD、AO。
（1）求证：CD∥AO；
（2）设CD=x，AO=y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3分）
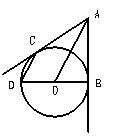（3）若AO+CD=11，求AB的长。
七、（本题满分12分）
22．如图1，O为圆柱形木块底面的圆心，过底面的一条弦AD，沿母线AB剖开，得剖面矩形ABCD，AD＝24 cm，AB＝25 cm．若
的长为底面周长的
，如图2所示．
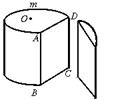
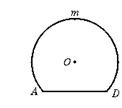
图1 图2
(1)求⊙O的半径；
(2)求这个圆柱形木块的表面积 (结果可保留根号)。
八、（本题满分14分）
23、如图，已知抛物线L1: y=x2-4的图像与x有交于A、C两点，
（1）若抛物线l2与l1关于x轴对称，求l2的解析式；
（2）若点B是抛物线l1上的一动点（B不与A、C重合），以AC为对角线，A、B、C三点为顶点的平行四边形的第四个顶点定为D，求证：点D在l2上；
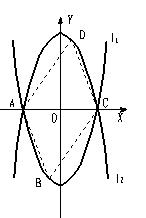（3）探索：当点B分别位于l1在x轴上、下两部分的图像上时，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由。
参考答案
一、1、C 2、B 3、B 4、B 5、D 6、B 7、B 8、B 9、A 10、A
二、11略 12 略 13、
； 14、B（4，0）、（ 
，2）、 C（4，3）、
（
）
三、
15、原式＝
＝2．
16、（1）
；y＝－x－1
（2）x<-2或0<x<1
17、（1）y＝2x2
（2）8；24.5
（3）5秒
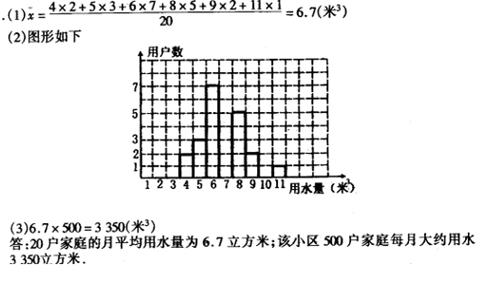18、
19、
 |  |
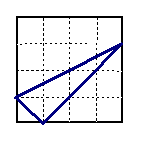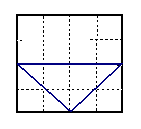
20、60°
21、（1）连接BC交OA于E点。
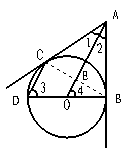∵AB、AC是⊙O的切线，
∴AB=AC, ∠1=∠2
∴AE⊥BC
∴∠OEB=90O。
∵BD是⊙O的直径
∴∠DCB=90O
∴∠DCB=∠OEB
∴CD∥AO。
(2)∵CD∥AO
∴∠3=∠4
∵AB是⊙O的切线，DB是直径
∴∠DCB=∠ABO=90O
∴△BDC∽△AOB。
∴=
∴=
∴y
=
，
∴0<x<6 。
(3)由已知和(2)知：
，
∴ 
，
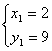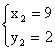（舍去）
∴AB===
。
22、(1)连结OA、OD作OE⊥AD于E，易知∠AOD＝120°，AE＝12 cm，可得
AO＝r＝
＝8
cm．
(2)圆柱形表面积2S圆＋S侧＝(384＋400) cm2．
23、解：设l2的解析式为y=a(x-h)2+k
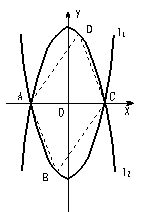∵l1与x轴的交点A(-2,0),C(2,0),顶点坐标是(0，-4),l2与l1关于x轴对称，
∴l2过A(-2,0),C(2,0),顶点坐标是（0，4） ∴y=ax2+4 。
∴0=4a+4 得 a=-1
∴l2的解析式为y=-x2+4
(2)设B(x1 ,y1)
∵点B在l1上
∴B(x1 ,x12-4)
∵四边形ABCD是平行四边形，A、C关于O对称
∴B、D关于O对称
∴D(-x1 ,-x12+4)。
将D(-x1 ,-x12+4)的坐标代入l2：y=-x2+4
∴左边=右边
∴点D在l2上。
(3)设平行四边形ABCD的面积为S,则
S=2S△ABC =ACy1=4y1
a.当点B在x轴上方时，y1＞0
∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大，
∴S既无最大值也无最小值。
b.当点B在x轴下方时，-4≤y1＜0
∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小，
∴当y1 =-4时，S有最大值16，但它没有最小值
此时B(0,-4)在y轴上，它的对称点D也在y轴上。