中考数学专题复习6:图象信息问题
Ⅰ、综合问题精讲:
图象信息题是指由图象(表)来获取信息.从而达到解题目的的题型,这类问题来源广泛,形式灵活,突出对考生收集、整理和加工信息能力的考查.是近几年中考的热点.解图象信息题的关键是“识图”和“用图”.解这类题的一般步骤是:(1)观察图象,获
取有效信息;(2)对已获信息进行加工、整理,理清各变量之间的关系;(3)选择适当的数学工具,通过建模解决问题.
Ⅱ、典型例题剖析
【例1】(2005,衢州)改革开放以来,衢州的经济得到长足发展近来,衢州市委市政府又提出“争创全国百强城市"的奋斗目枥己下面是衢州市1999--2004年的生产总值与人均生产总值的统计资料:

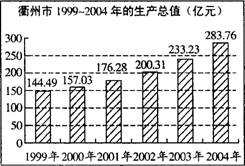
请你根据上述统计资料回答下列问题:
(1)1999—2004年间,衢州市人均生产总值增长速度最快的年份是 .这一年的增长率为 .
(2)从1999年至2004年衢州市的总人口增加了约 万人(精确到O.01).(3)除以上两个统计图中直接给出的数据以外,你还能从中获取哪些信息?请写出两条.
解:(1)2004,21.03%(2)4.51(3)参考信息例举:
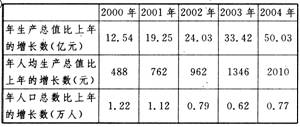 ①
①
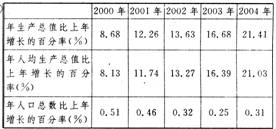 |
②
 ③
③
④跨年度比较的增长度和增长率的数据;
⑤从增长趋势分析的数据.
点拨:此题属于图表信息题,读懂两图的区别与联系,是解决此题的关键.
 【例2】(2005,河北课改区)在一次蜡烛燃烧实验中,甲、乙 两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图2-1-2所示。请根据图象所提供的信息解答下列问题:
【例2】(2005,河北课改区)在一次蜡烛燃烧实验中,甲、乙 两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图2-1-2所示。请根据图象所提供的信息解答下列问题:
⑴甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是_____;
⑵分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
⑶当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
解:⑴30cm,25cm;2h,2.5h;
⑵设甲蜡烛燃烧时y与x之间的函数关系式为![]() ,
,
由图可知,函数的图象过点(2,0),(0,30),
∴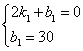 解得
解得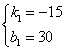
![]()
设乙蜡烛燃烧时y与x之间的函数关系式为![]() ,
,
由图可知,函数的图象过点(2.5,0),(0,25),
∴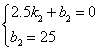 解得
解得
![]()
⑶由题意得![]() ,解得
,解得![]()
∴ 当甲、乙两根蜡烛燃烧1h的时候高度相等。
 点拨:要想求出一次函数解析式,关键是要找出图象上的两个关键点的坐标.这样我们就可以用待定系数法求出此函数的解析式了.
点拨:要想求出一次函数解析式,关键是要找出图象上的两个关键点的坐标.这样我们就可以用待定系数法求出此函数的解析式了.
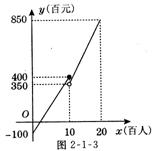
【例3】一次时装表演会预算中,票价定为每张 100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图2-1-3所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险费5000元(不列人成本费用人请解答下列问题:
(1)求当观众人数不超过1000人时,毛利润y关于观众人数的函数解析式和成本费用S(百元)关于观众人数x的函数解析式;
(2)若要使这次表演会获得36000。元的毛利润,那么需售出多少张门票?需支付成本费用多少元?
注:当观众人数不超过1000人时,表演会的毛利润一门票收人一成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入-成本费用-平安保险费.
解:(1)由图2-1-3知,当 0≤x≤10与10<x≤20时,y都是x的一次函数.
当0≤x≤10时,设y关于x的函数解析式为y=kx+b,把点(0,-100),(10,400)代入函数解析式,得
![]()
所以y=50x-100(0≤x≤10),
S=100x-(50x-100)=50x+100(0≤x≤10)
(2)当10<x≤20时,由题意,知 50x-100=360.
所以x=9.2,S=50x+100 =50×9.2+100=560.
当10<x≤2 0时,设y=mx+n.
把点(10,350)(20,850)代入函数解析式,得
![]()
所以y=50x-150(10<x≤20),
S=100x-(50x-150)-50=50x+100(10<x≤20)
当y=360时,50x-150=360,解得x=10.2.
所以S=50×10.2+100=610.
答:需售门票 920张或 1020张,相应地需支付成本费用分别为56000元或 61000元.
点拨:正确理解题意,注意单位的统一.
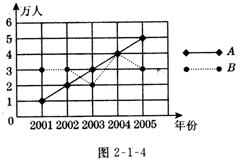 【例4】(2005,重庆)如图2-1-4所示,A、B两个旅游点从2001年至2005年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:
【例4】(2005,重庆)如图2-1-4所示,A、B两个旅游点从2001年至2005年“五、一”的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2001到2005年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人 数为4万人,为控制游客数量,A旅游点决定提高门票价格.已知门票价格x(元)与游客人数y(万人)满足函数关系![]() .若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
解:(1)B旅游点的旅游人数相对上一年增长最快的是2004年.
(2)![]() =
=![]() =3(万元)
=3(万元)
![]() =
=![]() =3(万元)
=3(万元)
![]() =
=![]() [(-2)
[(-2)![]() +(-1)
+(-1)![]() +0
+0![]() +1
+1![]() +2
+2![]() ]=2
]=2
![]() =
=![]() [0
[0![]() +0
+0![]() +(-1)
+(-1)![]() +1
+1![]() +0
+0![]() ]=
]=![]()
从2001至2005年,A、B两个旅游点平均每年的旅游人数均为3万人,但A旅游点较B旅游点的旅游人数波动大. (3)由题意,得5-![]() ≤4;
≤4;
解得x≥100, 100-80=20
答:A旅游点的门票至少要提高20元.
Ⅲ、综合巩固练习:(10分 90分钟)
一、选择题(每题3分,共24分)
1、一次函数y=kx+b和y=bx+k在同一坐标系内的图象大致是图2-l-5中的( ) (图2-l-5)

2.一次函数y=kx+b的图象如图2-1-6所示,则k中的值分别为( )
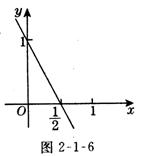 A、k=- b=1 B、k=-2 b=1
A、k=- b=1 B、k=-2 b=1
C、k= b=1 D、k=2 b=1
3.小明的父亲饭后出去散步,从家中走20分钟到一个离家900m的报亭看10分钟报纸后,用15分钟返回家里观图2d河中表示小明的父亲离家的时间与距离之间关系的是( ) (图2-l-7)
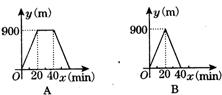
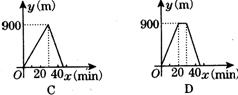
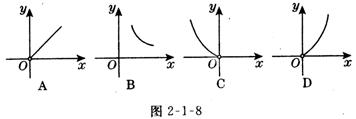
4.如图2-l-8所示,正方形的面积y与边长x之间的函数关系的大致图象是( )、
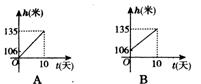
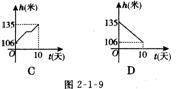
5.三峡工程在6月l日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡平湖初现人间,假设水库水位匀速上升,那么图2-l-8中,能正确反映这10天水位 h(米)随时间t(天)变化的是( )
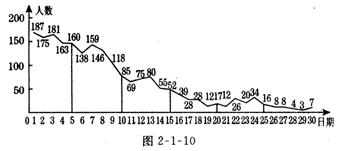
6.2003年春季,我国部分地区SARS流行,党和政府采取果断措施,防治结合,很快使病情得到控制.图2-l-10是某同学记载的5月1日到30日每天全国的SARS新增确诊病例数据图.将图中记载的数据每5天作为一组,从左至右分为第一组至第六
组,下列说法:①第一组的平均数最大,第六组的平均数最小;②第二组的中位数为138;③第四组的众数为28.其中正确的有( )
A.0个 B.l个 C.2个 D.3个
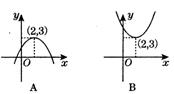
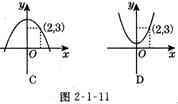
7.图2-l-11四个二次函数的图象,函数在x=2时有最大值3的是( )

8.图2-l-12是某报纸公布的我国“九·五”期间国内生产总值的统计图,那么“九·五”期间我国国内生产总值平均每年比上一年增长( )
A.0.575万亿元; B、0.46万亿元
C.9.725万亿元; D.7.78万亿元
二、填空题(每题4分,共28分)
9.二次函数y=x2+bx+c的图象如图2-l-13所示,则函数值y<0时,对应x的取值范围是_______.
10 二次函数y=ax2+(a-b)x—b的图象如图2-l-14所示,那么化简
![]() 的结果是_________________.
的结果是_________________.
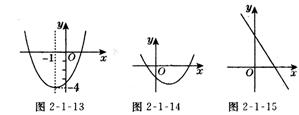
11若一次函数 y=kx+b的图象如图2-l-15所示,则抛物线 y=x2+kx+b的对称轴位于y轴的_____侧;反比例函数y= 的图象在_______象限内,
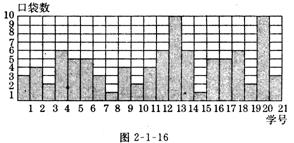
12图2-l-16表示某班21位同学衣服上口袋的数目,若任选一位同学,则其衣服上口袋数目为5的概率是___________.
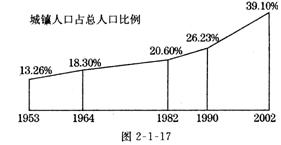
13 城镇人口占总人口比例的大小表示城镇化水平的高低,由图2-l-17的统计图可知,我国城镇化水平提高最快的时期是___________.
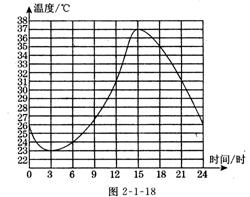
14 图2-l-18表示长沙市2003年6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
⑴ 这天的最高气温是_________℃;
⑵ 这天共有________个小时的气温在3loC以上;
⑶ 这天在________(时间)范围内温度在上升;
⑷ 请你预测一下,次日凌晨1点的气温大约是_____.
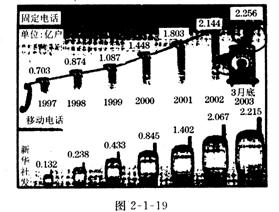
15 据信息产业部2003年4月公布的数字显示,我国固定电话和移动电话用户近年来都有大幅度增加,移动电话用户已接近固定电话用户.根据图2-l-19所示,我国固定电话从_______年至_______年的年增加量最大;移动电话从_______年至_______ 年的年增加量最大.
三、解答题(48分)
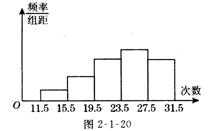 16.(9分)如图 2-l-20是某校初三年级部分学生做引体向上的成绩,进行整理后,分成五组画出的频率分布直方图,已知从左到右前四个小组的频率分别是0.05,0.15,0.25,0.30,第五小组的频数是25,根据已知条件回答下列问题:
16.(9分)如图 2-l-20是某校初三年级部分学生做引体向上的成绩,进行整理后,分成五组画出的频率分布直方图,已知从左到右前四个小组的频率分别是0.05,0.15,0.25,0.30,第五小组的频数是25,根据已知条件回答下列问题:
⑴ 第五小组的频率是多少?
⑵ 参加本次测试的学生总数是多少?
⑶ 如果做 20次以上为及格(包括20次),求此次测试及格的人数是多少?
17.(8分)某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、‘“优秀”三个等级,为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图 如图2-l-21所示.试结合图示信息回答下列问题:
如图2-l-21所示.试结合图示信息回答下列问题:
⑴ 这32名学生培训前考分的中位数所在的等级是_____,培训后考分的中位数所在的等级是_______;
⑵ 这32名学生经过培训,考分等级“不合格”的百分比由_______下降到_______;
⑶ 估计该校整个初二年级中,培训后考分等级为“合格”与“优 秀”的学生共有_______名;
⑷ 你认为上述估计合理吗?理由是什么?
答:_________.理由:_____________________.
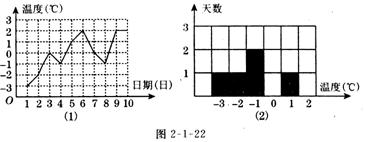
18.(5分)如图2-1-22⑴是某城市三月份1至10日的最低气温随时间变化的图象.
⑴ 根据图门)提供的信息,在图门)中补全直方图;
⑵ 这 10大最低气温的众数是℃,最低气温的中位数是______ ℃,最低气温的平均数是_______℃.
19.(6分)小亮家最近购买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知:用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)分别做了预算,通过列表,并用x(m)表示铺设地面的面积,用y(元)表示铺设费用,制成图2-1-23.
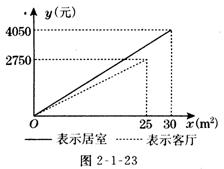
请你根据图中所提供的信息,解答下列问题:
⑴ 预算中铺设居室的费用为______元/m2,铺设客厅的费用为_________元/m2;
⑵ 表示铺设居室的费用y(元)与面积x(m)之间的函数解析式为___________,表示铺设客厅的费用y(元)与面积x(m)之间的函数解析式为________________;
⑶ 已知小亮在预算中,铺设1m2的瓷砖比铺设1m2木质地板的工钱多 5元;购买1m2的瓷砖是购买1m2木质地板费用的,那么,铺设每平方米木质地板、瓷砖的工钱各是多少元?购买每平方米的木质地板、瓷砖的费用各是多少元?
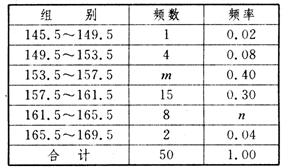
20. (8分)为了了解初三学生身体发育情况,某中学对初三女学生的身高进行了一次测量,所得数据整理后列出了频率分布表:
⑴ 表中m和n所表示的数分别是多少?
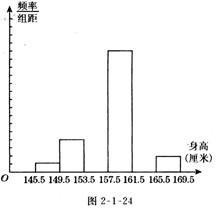
⑵ 补全图2-l-24中频率分布直方图.

21 (12分)某班同学进行数学测验,将所得成绩(得分取整数)进行整理后分成五组,并绘制成频率分布直方图(图2-l-25所示).请结合直方图提供的信息,回答下列问题:
⑴ 该班共有多少名学生?
⑵ 用0.5~90.5这一分数段的频数,频率分别是多少?
⑶ 这次成绩中的中位数落在哪个分数段内?
⑷ 从左到右各小组的频率比是多少?