《整式的乘除》基础测试

《整式的乘除》基础测试

（一）填空题（每小题2分，共计20分）

1．x¹⁰＝（－x³）²·_________＝x¹²÷x^（　　）【答案】x⁴；2．

2．4（m－n）³÷（n－m）²＝___________．【答案】4（m－n）．

3．－x²·（－x）³·（－x）²＝__________．【答案】x⁷．

4．（2a－b）（）＝b²－4a²．【答案】－2a－b．

5．（a－b）²＝（a＋b）²＋_____________．【答案】－4ab．

6．（）^－2＋p⁰＝_________；4¹⁰¹×0.25⁹⁹＝__________．【答案】10；16．

7．20×19＝（　　）·（　　）＝___________．【答案】20＋，20－，399．

8．用科学记数法表示－0.＝___________．

　　【答案】－3.08×10^－5．

9．（x－2y＋1）（x－2y－1）²＝（　　）²－（　　）²＝_______________．

　　【答案】x－2y，1x²－4xy＋4y．

10．若（x＋5）（x－7）＝x²＋mx＋n，则m＝__________，n＝________．【答案】－2，35．

（二）选择题（每小题2分，共计16分）

11．下列计算中正确的是…………………………………………………………………（　　）

（A）aⁿ·a²＝a²ⁿ （B）（a³）²＝a⁵ （C）x⁴·x³·x＝x⁷ （D）a^2n－3÷a^3－n＝a^3n－6

　　【答案】D．

12．x^2m＋1可写作…………………………………………………………………………（　　）

（A）（x²）^m＋1 （B）（x^m）^2＋1 （C）x·x^2m （D）（x^m）^m＋1【答案】C．

13．下列运算正确的是………………………………………………………………（　　）

（A）（－2ab）·（－3ab）³＝－54a⁴b⁴

（B）5x²·（3x³）²＝15x¹²

（C）（－0.16）·（－10b²）³＝－b⁷

（D）（2×10ⁿ）（×10ⁿ）＝10²ⁿ【答案】D．

14．化简（aⁿb^m）ⁿ，结果正确的是………………………………………………………（　　）

（A）a²ⁿb^mn （B）　 （C）　 （D）

　　【答案】C．

15．若a≠b，下列各式中不能成立的是………………………………………………（　　）

（A）（a＋b）²＝（－a－b）² （B）（a＋b）（a－b）＝（b＋a）（b－a）

（C）（a－b）²ⁿ＝（b－a）²ⁿ（D）（a－b）³＝（b－a）³

　　【答案】B．

16．下列各组数中，互为相反数的是……………………………………………………（　　）

（A）（－2）^－3与2³ （B）（－2）^－2与2^－2

（C）－3³与（－）³ （D）（－3）^－3与（）³

　　【答案】D．

17．下列各式中正确的是………………………………………………………………（　　）

（A）（a＋4）（a－4）＝a²－4　　　 （B）（5x－1）（1－5x）＝25x²－1

（C）（－3x＋2）²＝4－12x＋9x² （D）（x－3）（x－9）＝x²－27

　　【答案】C．

18．如果x²－kx－ab＝（x－a）（x＋b），则k应为…………………………………（　　）

（A）a＋b　 （B）a－b　 （C）b－a　 （D）－a－b

　　【答案】B．

（三）计算（每题4分，共24分）

19．（1）（－3xy²）³·（x³y）²；　【答案】－x⁹y⁸．

（2）4a²x²·（－a⁴x³y³）÷（－a⁵xy²）；【答案】ax⁴y．

（3）（2a－3b）²（2a＋3b）²；【答案】16a⁴－72a²b²＋81b⁴．

（4）（2x＋5y）（2x－5y）（－4x²－25y²）； 【答案】625y⁴－16x⁴．

（5）（20a^n－2bⁿ－14a^n－1b^n＋1＋8a²ⁿb）÷（－2a^n－3b）；【答案】－10ab^n－1＋7a²bⁿ－4a^n＋3．

（6）（x－3）（2x＋1）－3（2x－1）²．

　　　 【答案】－10x²＋7x－6．

20．用简便方法计算：（每小题3分，共9分）

（1）98²；

　　　 【答案】（100－2）²＝9604．

（2）899×901＋1；

　　　 【答案】（900－1）（900＋1）＋1＝900²＝810000．

（3）（）²⁰⁰²·（0.49）¹⁰⁰⁰．

　　　 【答案】（）²·（）²⁰⁰⁰·（0.7）²⁰⁰⁰＝．

（四）解答题（每题6分，共24分）

21．已知a²＋6a＋b²－10b＋34＝0，求代数式（2a＋b）（3a－2b）＋4ab的值．

【提示】配方：（a＋3）²＋（b－5）²＝0，a＝－3，b＝5，

【答案】－41．

22．已知a＋b＝5，ab＝7，求，a²－ab＋b²的值．

【答案】＝[（a＋b）²－2ab]＝（a＋b）²－ab＝．

a²－ab＋b²＝（a＋b）²－3ab＝4．

23．已知（a＋b）²＝10，（a－b）²＝2，求a²＋b²，ab的值．

　　【答案】a²＋b²＝[（a＋b）²＋（a－b）²]＝6，

ab＝[（a＋b）²＋（a－b）²]＝2．

24．已知a²＋b²＋c²＝ab＋bc＋ac，求证a＝b＝c．

　　【答案】用配方法，a²＋b²＋c²－ab－bc－ac＝0，∴　2（a²＋b²＋c²－ab－ac－bc）＝0，

即（a－b）²＋（b－c）²＋（c－a）²＝0．∴　a＝b＝c．

（五）解方程组与不等式（25题3分，26题4分，共7分）

25．

　　【答案】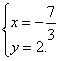

26．（x＋1）（x²－x＋1）－x（x－1）²＜（2x－1）（x－3）．

　　【答案】x＞－．