一元二次方程根与系数之间的关系Ⅱ

中考数学辅导之—一元二次方程根与系数之间的关系Ⅱ

上期,我们学习了一元二次方程根与系数之间的关系.

即若x₁,x₂是ax²+bx+c=0(a≠0)的两根,则有

此定理的应用我们讲了第一种,即不解方程求某些代数式的值,如已知的两实根,求的值.在此专题中,还有一题.

例:已知2x²-3x-1=0的根是x₁,x₂求x₁-x₂的值.

分析:∵由二次根式的性质,反之,因此将可化为求.

解:

有了这个例题,求代数式的值的类型都可解决.第二种用法是利用根与系数间的关系求某些字母的值.

例1. 已知关于x的一元二次方程.

解:

　

　

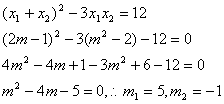
是x²-9x+23=0此时Δ=(-9)²-4×23=81-92=-11<0

方程无实根　∴m=-1

小结:此题的两根之和与两根之积是含m的代数式.由已知条件配方成代入两根之和与两根之积,化为含有m的一元二次方程,解方程求出m的值,还要检验方程的根是否都适合题意.

例2: 已知一元二次方程x²-2kx-5+2k=0的两根是x₁,x₂且求k的值.

解:由韦达定理得:x₁+x₂=2k,x₁·x₂=2k-5

两边平方得:(x₁-x₂)²=32

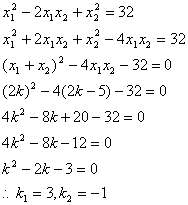
经检验k₁=3和k₂=-1都适合题意.

例3: 已知m是正实数,关于x的方程2x²-mx-30=0的两根是x₁,x₂,且5x₁+3x₂=0且5x₁+3x₂=0求m的值.

解:由根与系数间的关系可得 ①

　　　　　　　　　　　　  ②

　 由已知条件5x₁+3x₂=0 ③

解:①③组成的方程组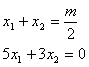

解得: 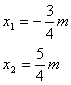将方程组的解代入②得

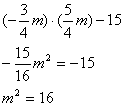
m=4或m=-4　　∵m是正实数  ∴m=4

上述三个例题的已知条件都有一个:例1中是;例2有条件;例3中有5x₁+3x₂=0.

但每题都有隐含条件即.这样每题匀有三个条件,将这三个条件很好运用,就可求出m或k.此种应用是根与系数间的关系习题中经常遇到的,应很好掌握.

第三种应用:求一个新方程,使这个新方程的根与原方程的根有某些关系.

如果方程x²+px+q=0的根是x₁,x₂,那么x₁+x₂=-p,x₁·x₂=q

p=-(x₁+x₂), q=x₁·x₂代入x²+px+q=0

得x²-(x₁+x₂)x+x₁·x₂=0

这就是以两个数x₁,x₂为根的一元二次方程.

(注意:方程的一次项系数是两数和的相反数,常数项是两数之积).

例1. 求一个一元二次方程,使它的两根分别是:

①　　②

分析:就是方程的根x₁,x₂,代入方程公式

①解:以为根的方程是

　　

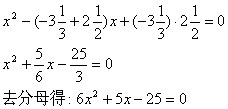
②解:以为根的方程是

　　

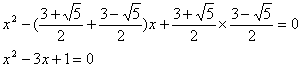
例2. 已知方程

求作一个新方程,使它的根分别是原方程的根的平方.

分析:x₁,x₂是原方程的根,

　　 则

设新方程的根是y₁,y₂(注意设新方程的极是y₁,y₂是因为要与原方程的根x₁,x₂有所区别.)

解:设新方程的极是y₁,y₂,由题意得

　 (新方程的根是原方程根的平方)

以y₁,y₂为根的方程是y²-(y₁+y₂)y+y₁·y₂=0

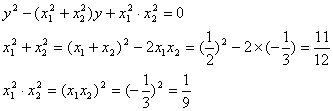
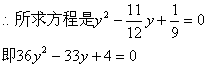
例3. 已知方程5x²+2x=3求作一个方程,使它的根是原方程根的负倒数.

解:设原方程根是

　 新方程的根是

　 所求方程是

　

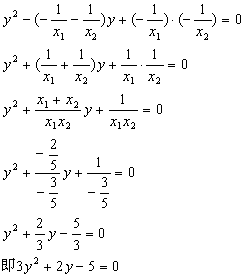
本次练习

一、解答下列问题

1.已知x₁,x₂是方程x²-2(2m+1)x+3m²-4=0的根,且.求m的值.

2.已知方程2x²+mx-2m+1=0的两个根的平方和是.求m的值.

3.已知方程x²+(2k+1)x+k²-2=0的两实根的平方和是11.求k的值.

4.已知方程(m+2)x²-8mx-(2m-1)=0的两根互为负倒数.求m的值(提示:两根互为负倒数,是两根之积是-1).

二、求以下列两数为根的方程

　1.　　2.

三、不解方程求作一个新的一元二次方程,使它的根分别满足下列条件

1.已知方程4x²-3x-1=0,求作一个新方程,使它的根分别是原方程根的相反数.

2.已知方程6x²-3x-2=0,求作一个新方程,使它的根分别是原方程根的倒数.

3.已知方程2x²-5x=2,求作一个新方程,使它的根是原方程根的平方.

4.已知方程2x²=7-5x,求作一个新方程,使它的根比原方程的根大3.

5.已知方程2x²-x-7=0,求作一个新方程,使它的根分别是原方程根的3倍.

6.已知方程x²-3x+1=0,求作一个新方程,使它的根分别是原方程根的平方的倒数.

本期练习答案

一、1.　 2.3(-11舍去)　 3.1(-3舍去)　 4.m=3

二、1.　　2.

三、1.　　2.　　3.

　　4.　 5.　 6.