中考数学模拟试题4

中考数学模拟试题4

班级：_________　姓名：_________　得分：_________

一、填空题(每小题3分，共24分)

1．若二次三项式x²＋4x＋k在实数范围内可以分解为两个一次式的积，则k的取值范围是______．

2．如果a∶3＝b∶4，那么的值是______．

3．如图1，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数为______．

　　

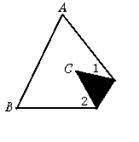
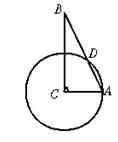
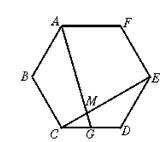
图1　　　　　　  图2　　　　　　　　　  图3

4．观察下列算式：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，2⁶＝64，2⁷＝128，2⁸＝256，…通过观察，用你所发现的规律写出8⁹的末位数字是______．

5．如图2，在△ABC中，∠ACB＝90°，∠B＝25°，以C为圆心，CA为半径的圆交AB于D，则的度数是______．

6．如果实数A、B、C满足A＋B＋C＝0，那么直线Ax＋By＋C＝0一定过点______．

7．如果关于x的一元二次方程2x²＋3x＋5m＝0的两个实数根都小于1，那么实数m的取值范围是______．

8．如图3，G是正六边形ABCDEF的边CD的中点．连结AG交CE于点M，则GM∶MA＝______．

二、选择题(每小题3分，共15分)

9．若函数y＝k₁x(k₁≠0)和函数y＝(k₂≠0)在同一坐标系内的图象没有公共点，则k₁和k₂(　)

　　A．互为倒数　　B．符号相同　　C．绝对值相等　　D．符号相反

10．某村办工厂今年前五个月生产某种产品的总量c(万件)与时间t(月)的函数图象如图4所示，则该厂对这种产品来说(　)

　　A．1月至3月每月生产总量逐月增加，4、5两月每月生产总量逐月减少;

　　B．1月至3月每月生产总量逐月增加，4、5两月生产总量与3月持平;

　　C．1月至3月每月生产总量逐月增加，4、5两月均停止生产;

　　D．1月至3月每月生产总量不变，4、5两月均停止生产.

11．如图5，在矩形ABCD中，DE⊥AC于E，设∠ADE＝a ，且cosa ＝，AB＝4，则AD的长为(　)

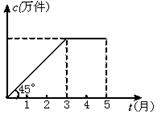
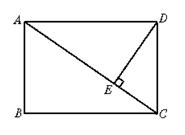
图4　　　　　　　　　　  图5　　　　　　　　　　　  图6

　　A．3　　　　　　　　　　　　　　　　　 B．　　C．　　　　　　　　　　　　　　D．

12．一位美术老师在课堂上进行立体模型素描教学时，把14个棱长为1分米的正方体摆在课桌上成如图6形式，然后他把露出的表面都涂上不同的颜色，则被他涂上颜色部分的面积为(　)

　　A．33分米²B．24分米²　　C．21分米² D．42分米²

13．已知：关于x的一元二次方程x²-(R＋r)x＋d²＝0无实数根，其中R、r分别是

⊙O₁、⊙O₂的半径，d为此两圆的圆心距，则⊙O₁，⊙O₂的位置关系为(　)

　　A．外离 　　　　　　　　　　 B．相切　　C．相交　　　　　　　　　　　　D．内含

三、解答题(14～15每题6分，16～19每题9分，共48分)

14．计算：sin60°----()^-1．

15.化简求值:,其中_.

16．A、B两地间的路程为150千米，甲、乙两车分别从A、B两地同时出发，相向而行，2小时相遇；相遇后，各以原来速度继续行驶，甲车到达B地立即原路返回，返回时的速度是原来的2倍，结果甲乙两车同时到达A地，求甲车的原速度和乙车的速度．

17．已知：关于x的一元二次方程x²＋2x＋2-m＝0(1)，若方程有两个不相等的实数根，求实数m的取值范围；并利用你所得的结论，任取m的一个数值代入方程(1)，并用配方法求出此方程的两个实数根．

18．如图,地面上有不在同一直线上的A、B、C三点，一只青蛙位于地面异于A、B、C的P点，第一步青蛙从P跳到P关于A的对称点P₁，第二步从P₁跳到P₁关于B的对称点P₂，第三步从P₂跳到P₂关于C的对称点P₃，第四步从P₃跳到P₃关于A的对称点P₄……以下跳法类推。问:

（1）青蛙能否跳回到原处P？如果能，请作图并回答至少跳几步回到原处P？

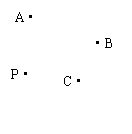（2）青蛙跳完第2005步落在地面什么位置？

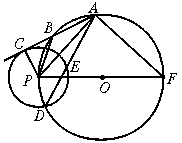
19．如图，点P是⊙O上任意一点，⊙O的弦AB所在的直线与⊙P相切于点C，PF为⊙O的直径，设⊙O与⊙P的半径分别为R和r．

　　(1)求证：△PCB∽△PAF； (2)求证：PA·PB＝2Rr；

　　(3)若点D是两圆的一个交点，连结AD交⊙P于点E，当R＝3r，PA＝6，PB＝3时，求⊙P的弦DE的长．

四、解答题(本大题只有1题，满分13分)

20．某衡器厂的RGZ-120型体重秤，最大称量120千克，你在体检时可看到如图显示盘．已知，指针顺时针旋转角x(度)与体重y(千克)有如下关系：

　　(1)根据表格的数据在平面直角坐标系中描出相应的点，顺次连结各点后，你发现这些点在哪一种图象上？合情猜想符合这图形的函数解析式．

　　(2)验证这些点的坐标是否满足函数解析式，归纳你的结论(写出自变量x的取值范围)；

　　(3)当指针旋转到158.4度的位置时，显示盘上的体重读数模糊不清，用解析式求出此时的体重．

k(度)	0	72	144	216
Y(千克)	0	25	50	75

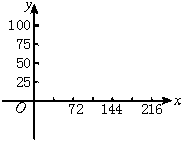
图10　　　　　　  图11

参考答案

一、1．Δ＝16-4k≥0，∴　k≤4　2．　3．60°　4．8　5．50°

6．P(1，1)　

提示：(1)特例法：取满足A＋B＋C＝0的两组数，

如A＝1，B＝0，C＝-1，得x-1＝0，

∴　x＝1，再取A＝0，B＝1，C＝-1，得y-1＝0，

∴　y＝1，∴　过定点即P(1，1)．

　　(2)把A＝-(B＋C)代入Ax＋By＋C＝0中，有(y-x)B＋(1-x)C＝0，

　　∴　得P(1，1)．

7．-1＜m≤　提示：Δ＝9-40m≥0，∴　m≤　　　　　　　　　　　　 ①

　　方法一：x＝＜1，∴　m＞-1

　　方法二：记y＝f(x)＝2x²＋3x＋5m，

　　∴　由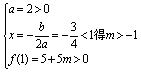　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

　　由①②得：-1＜m≤．

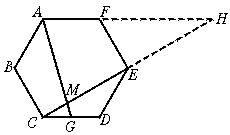
8．1∶6　提示：延长AF与CE的延长线交点H．

　　∵　∠CEF＝90°，∠AFE＝120°，∴　∠H＝30°，得FH＝2EF，

　　∴　AH＝3AF，∵　△AMH∽△GMC，

　　∴　AM∶GM＝AH∶CG＝3∶，

　　即GM∶MA＝1∶6．

二、9．D　10．D　11．B　12．A　13．C

三、14．-2

15．不等式组的解集是2＜x≤4，∴　不等式组的整数解是3，4．

16．设甲车的原速度为x千米/时，乙车的原速度为y千米/时，则

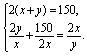　　解得

17．解：∵　方程有两个不相等的实数根，∴　Δ＞0，

　　Δ＝4-4(2-m)＝4m-4＞0，∴　m＞1．

　　例如：取m＝2，则有x²＋2x＝0，配方，得(x＋1)²＝1，解得x₁＝-2，x₂＝0

18．解：在图(1)中，B(4，0)、C(4，3)；

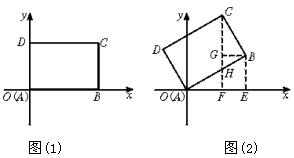
在图(2)中，分别过点B、C作x轴的垂线，垂足分别为E、F，过B作BG⊥CF于G，则有在Rt△ABE中，OE＝ABcos30°＝4×＝2，BE＝ABsin30°＝4×＝2，

∴　B(2，2)．

　　设AB与CF交于点H，

　　则由∠ABC＝∠AFH，∠AHF＝∠CHB，得∠BCG＝∠BAE＝30°，

　　在Rt△BGC中，BG＝BCsin30°＝3×＝

　　∴　OF＝OE-FE＝OE-BG＝2-＝，

　　CF＝CG＋GF＝CG＋BE＝＋2＝，

　　∴　C(，)．

19．(1)略　(2)证△PCB∽△PAF即可．

(3)连PD，过点P作PH⊥DE于H点．

易知△CBP∽△HDPPH·PB＝PC·PD＝r²PH＝．

　　又PA＝6，PB＝3，所以2Rr＝18，易得r＝，R＝3，所以PH＝1，DH＝，所以DE＝2．

四、20．(1)符合这个图形的函数解析式为：y＝kx(k＝0)．

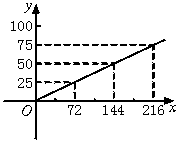
　　(2)将x＝72，y＝25代入，得25＝72k，即k＝，∴　y＝x　　　　　　　　　　　　　　 ①

　　验证：将其他两对分别代入①式，均满足．

　　∴　符合要求的函数解析式是y＝x由题意知， 0≤y≤120，0≤x≤120，解得0≤x≤345.6，即自变量x的取值范围是0≤x≤345.6．

　　(3)当x＝158.4度时，y＝·158.4＝55(千克)，即此时的体重为55千克．