中考数学辅导之—圆及相关定理、概念
继期中考试前我们讲了并且复习了垂径定理后,近期我们又学习圆心角,弧,弦,弦心矩之间的关系定理及推论.圆周角定理及推论.本次,我们将着重学习这两个定理.
一、1.圆心角及它所对的弧,弦,弦心距之间的关系由定理的推论说的很明白.即在同圆和等圆中,两个圆角角它所以的弧,弦,弦心距有一组量相等,基它各组量也分别相同.辟如说:若证明弧相等,即可证两条弧所对的圆心角相等,也可证弦相等.
2.圆周角定理的两个推论很重要.
圆周角定理:
1.一条弧上的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等,在同圆和等圆中,相等的圆周角也相等.此推论是说明在同圆和等圆中,弧等,圆周角等,圆周角相等它们所对的弧相等.在证明中,往往从角找它所对的弧,在从此弧找另一个圆周角,从而证两个圆周角相等.
推论2:直径(半圆)所对的圆周角是直角,90°的圆周角所对的弦是直径.
这个推论一段是若已知是直径,通常做直径上的圆周角,证得是直角.
二、本次练习:
(一)填空题
1.
圆内的一条弦把圆分成度数之比为1:5的两段弧,则该弦的弦心距与半径之比是______.
2.ΔABC内接于⊙O且BC:AC:AB=3:2:4,则∠A=______度,∠B=______度.
3.
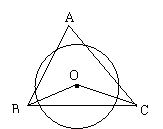⊙O的一弦AB将⊙O分成1:2的两段弧,则弦AB所对的圆心角是______度,所对的圆周角是______度.
4. 如图:在ΔABC中,∠A=70°,⊙O截
ΔABC的三边,截得的三条弦相等,则
∠BDC=______度.
5.
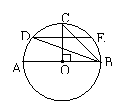如图:AB是⊙O的直径,半径OC⊥AB,
F是OC中点,弦DE∥AB,且F在DE上,则
∠CBD的度数是______度.
6.
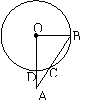
已知⊙O中,OA⊥OB,∠A=40°,
则CD的度数是______度.
 |
7.如图:∠B=25°,∠APB=80°,
则∠D=______度.
 |
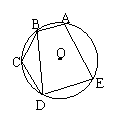8.如图:已知⊙O的内接五边形ABCDE,
AB=BC=DC,∠BDC=25°,则∠ABD的度数
是______度.
 |
9.如图:AD是直径,B是弦AC上一点,且
OB=5,∠ABC=60°,∠COD=60°,则BC的长
是______.
 |
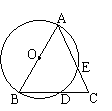10.已知:ΔABC中,AB=AC,以AB为直径
做圆交AC,BC于E,D.∠B=70°,则AE等于
______度,DE等于______度,BD等于______度.
 |
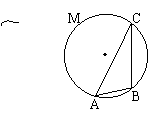
11.已知:ΔABC内接于⊙O,⊙O的半径
是6cm,∠B=45°,则AC=______.
 |
12.弦AB等于⊙O的半径,C是AMB
上任一点,则sinC=______.
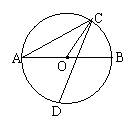
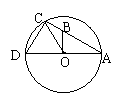
13.直径AB和弦CD相交.若AC和BC的度数
比是2:1,D是AB中点,则∠OCD的度数是______度.
(二)选择填空
1.已知:点O是ΔABC的外心,∠A=
,则∠BOC等于:
A.2 B.360°-2 C.2或360°-2
D.180°-2
2.
在⊙O中,AB=2CD,则AB与CD的关系是:
A.AB=2CD B.AB>2CD C.CD<AB<2CD D.不确定
3.在ΔAOB中,∠O=90°,以OB为半径的⊙O分别交AB,AO与C,D.∠A=28°,则CD的度数是:
A.28° B.56° C.62° D.34°
4.ΔABC内接于⊙O,OD⊥BC于D,∠BOD=38°,则∠A等于:
A.19° B.38°或142° C.19°或161° D.38°
5.在⊙O中,两条直径AB⊥CD于O,弦AP交CD于Q,则AP·AQ等于:
A.AO·OB B.CQ·QD C.AO·AB D.OQ·BP
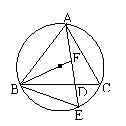(三)证明题
1.ΔABC中,∠A的平分线交BC于D.交
ΔABC外接圆于E.∠ABC的平分线交AD于F.
求证:BE=EF.
2.
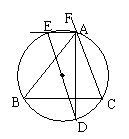已知在ΔABC中,∠A的内,外角平分线
分别交ΔABC的外接圆于D,E.
求证:DE垂直平分BC.
 |
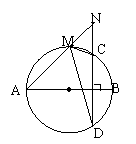3.AB是⊙O的直径,弦CD⊥AB,M是AC
上一点,延长AM,DC交于N.
求证:∠AMD=∠NMC
三、本次练习答案
(一)填空题
1.
2.60°,40° 3.120°,60°或120° 4.125° 5.30°
6.10° 7.55° 8.105° 9.5 10.100°,
40°, 40° 11.
12.
13.15°
(二)选择填空
1.C 2.C 3.D 4.B 5.C
(三)证明题
1.
略
2.证ED是直径,∵AD平分∠BAC,∴BD=CD 结论成立.
3.连MB,证∠BMC=∠DMB.