中考数学模拟试卷（一）

中考数学模拟试卷（一）

（满分：150分　　时间：120分钟）

一、选择题（本题共12小题，下列各小题的四个选项中，只有一个符合题意.每小题3分，共36分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

1．－2的倒数是

A．－2　　　　　  B．2　　　　　  　　 C．　　　　　　  D．－

2．方程x²＝x的根是

A．0　　　　　　  B．1　　　　　　 　 C．0，1　　　　　  D．0，－1

3．A车站到B车站之间还有3个车站，那么从A车站到B车站方向发出的车辆，一共有多少种不同的车票

A．8　 　　　　 　　　B．9　　　　　　 　　　C．10 　　　　　　　　　　D．11

4．实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为0.m，则这个数用科学记数法表示是

A．0.156×10^－5　　 B．0.156×10⁵　　 　C．1.56×10^－6　 　　　　D．1.56×10⁶

5．已知直角三角形的两条直角边的长恰好是方程x²－5x＋6＝0的两根，则此直角三角形的斜边长为

A．　　 　　　　　　B．3　　　　 　　　　 C．　　　　 　　　 D．13

6．已知∠AOB＝30°，点P在∠AOB内部，P₁与P关于OB对称，P₂与P关于OA对称，则P₁，O，P₂三点所构成的三角形是

A．等边三角形　　 B．等腰三角形　　 C．钝角三角形　　 　 D．直角三角形

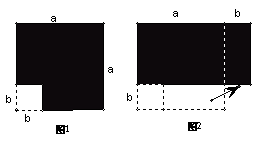7．在边长为a的正方形中挖去一个边长为b的小正方形（a>b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证

A．(a＋b)²＝a²＋2ab＋b²　　　　

B．(a－b)²＝a²－2ab＋b²　　 　　　　

C．a²－b²＝(a＋b)(a－b)　　　　 

第7题图

D．(a＋2b) (a－b)＝a²＋ab－2b²

8．如图是用直尺和圆规作角的平分线的示意图，说明射线OC

是∠AOB的平分线的根据是（　  ）

A．SAS　　　　　 　　　　　　 B．SSS

C．AAS　　　　 　　　　　　　　D．ASA

9．二次函数y＝－2（x－1）（x＋3）图象的顶点坐标为

A．（－1，8）　　　B．（－1，－8）　　　　C．（－2，－8）　　D．（－2，－8）

10．不等式组的解集在数轴上可以表示为

A．　　　　　 　 B．　　　　　　 　　　 C．　　　　　　 　　　 D．

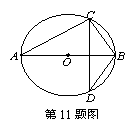11．如图，已知AB是⊙O的直径，CD是弦且CD⊥AB，BC＝6，

AC＝8，则sin∠ABD的值是

A．　　　　　　　　　　　 B．　

C．　　　　　　　　　　D．

12．在“五·一”黄金周期间，某超市推出如下购物优惠方案：（1）一次性购物在100元（不含100元）以内时，不享受优惠；（2）一次性购物在100元（含100元）以上，　300元（不含300元）以内时，一律享受九折的优惠；（3）一次性购物在300元（含300元）以上时，一律享受八折的优惠．王茜在本超市两次购物分别付款80元、252元．如果王茜改成在本超市一次性购买与上两次完全相同的商品，则应付款

　 Ａ．332元　　 Ｂ．316元或332元　　　　 Ｃ．288元　　Ｄ．288元或316元

二、填空题（本题共6小题，每小题4分，共24分）

13．写出一个你熟悉的且满足条件2＜a＜4的无理数a＝　　　　　 ．

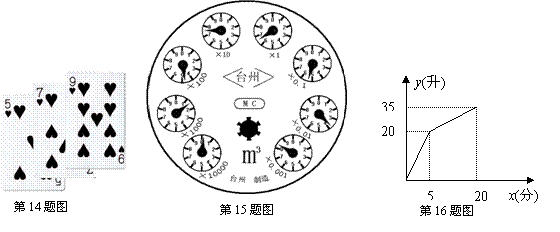
14．如图，在这三张扑克牌中任意抽取一张，抽到“红桃7”的概率是　　　．

15．小明家的水表如图所示，该水表的读数为　　　　　　　 （精确到0.1）．

16．有一个附有进水管和出水管的容器，在单位时间内的进水量和出水量分别一定．设从某时刻开始的5分钟内只进水不出水，在随后的15分钟内既进水又出水,得到容器内水量 (升)与时间 (分)之间的函数图象如上图．若20分钟后只放水不进水,这时(≥20时) 与之间的函数关系式是　　　　　　　　　　　　 　　　　　　 .

(请注明自变量的取值范围)

17．已知“”是一种运算符号，若______.

18．糖果盒是长方体，若长10厘米，宽6厘米，高2厘米，李明买了2盒，若外加包装，则最省外包装的用纸是　　　　　　 平方厘米(压边不算)．

三、解答题（解答应写出必要的计算过程、推演步骤或文字说明，共90分）

19．（本题满分6分）

先化简后求值：，其中．

20．（本题满分6分）

在平面直角坐标系中，已知点A（－1，3），B（－3，1），某函数y的图象经过点A、B．试写出经过A、B两点的函数解析式（要求：①写出2个不同类型的函数解析式；②写出必要的求解过程）．

21．（本题满分8分）

如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你在其中选3个作为题设，余下的1个作为结论，写一个真命题，并加以证明．

①AB=DE，②AC = DF，③∠ABC=∠DEF，④BE=CF．

已知：

求证：

证明：

22．（本题满分8分）

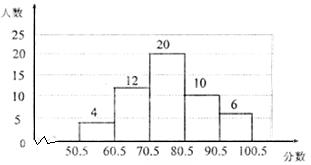
某校为了推动信息技术的发展，举行了电脑设计作品比赛，各班派学生代表参加，现将所有比赛成绩（得分取整数，满分为100分）进行处理然后分成五组，并绘制了频数分布直方图，请结合图中提供的信息，解答下列问题：

　　（1）参加比赛学生的总人数是多少?

　　（2）80.5～90.5这一分数段的频数、频率是多少?

　　（3）这次比赛成绩的中位数落在哪个分数段内?

（4）根据统计图，请你也提出一个问题，并做出回答.

23．（本题满分8分）

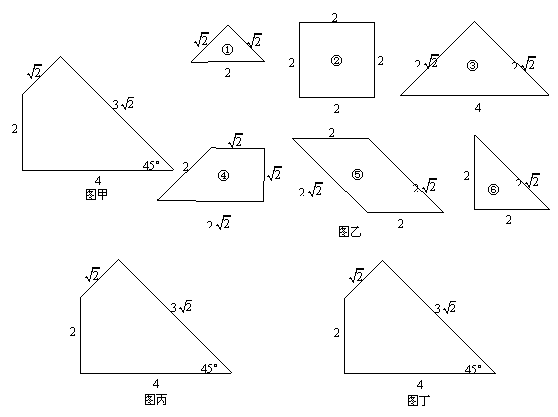小明家用瓷砖装修卫生间，还有一块墙角面未完工（如图甲所示），他想在现有的六块瓷砖余料中（如图乙所示）挑选2至3块余料进行辅设，请帮助小明设计两种不同的设计方案（在下图丙、丁中画出辅设示意图，并标出所选用每块余料的编号）．

 

24．（本题满分10分）

某厂生产一种零件，每个零件的成本为40元，出厂单价为60元，该厂为鼓励销售商订购，决定当一次订购超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.

（1）当一次订购量为多少个时，零件的出厂单价恰好降为51元？

（2）设一次订购量为x个，零件的实际出厂单价为P元，写出P与x的函数关系式；

（3）当销售商一次订购500个零件时，该厂获利润是多少元？如果订购1000个时，利润又是多少元？（工厂售出一个零件的利润=实际出厂单价－成本）

 

25．（本题满分10分）

如图，△AOB沿轴向右平移3个单位后，得到△A₁O₁B₁．

（1）求△A₁O₁B₁的三个顶点坐标；

（2）求经过O、A₁、_、B₁三点的抛物线解析式；

（3）画出△A₁O₁B₁以点O₁为中心，旋转180°以后的图形.

 

26．（本题满分10分）

PA、PB切⊙O于A、B，AC为⊙O的直径，AC与PB的延长线相交于M．

（1）若⊙O的半径为R，用R的代数式表示BC·OP；

（2）设MB＝a，MC＝b，PA＝c，请你思考后，选用一组适当的a、b、c的值，设计出计算⊙O半径R的一种方案．

你选用的a、b、c的值是　　　　 　　　　　．

27．（本题满分12分）

为了奋战十运会，有男、女两名运动员在长为50m的泳池中进行训练，他们分别以不同的泳姿同时同向出发，下图中的实线、虚线分别为男、女两运动员与出发点的距离随游泳时间的变化而变化的图象（转身时间不计），那么，

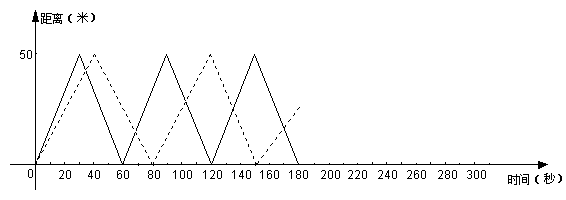
（1）男运动员游泳的平均速度是　　　　  ；女运动员游泳的平均速度是　　　 ．

（2）他们第一次相遇时，一共游了　　　 米；

（3）如果他们继续匀速游下去，请你预测一下：在　　　 秒时，他们会在起点处第一次相遇，在此之前，他们在途中先后相遇　　  次．并请你将此时的图象补充完整；

（4）求出发多少时间两名运动员第四次相遇？此时距出发点多远？

28．（本题满分12分）

矩形ABCD中，AD=8厘米，AB=24厘米，半径都是5厘米的圆⊙O₁、⊙O₂同时分别以2厘米／秒和1厘米／秒的速度从A、C两点出发，⊙O₁的运动路线是A→B→C→D→A，⊙O₂的运动路线C→D→A，设两圆运动的时间为t秒．

（1）当t取何值时，⊙O₁和⊙O₂第一次相切？

（2）在0≤t≤32的范围内⊙O₁和⊙O₂一共相切了几次？分别求出相应的t值；

（3）在0≤t≤32的范围内，当t取何值时⊙O₁和⊙O₂相交？