中考数学模拟试题(二)A
班级 座号 姓名 成绩
一、填空题(本题共10小题,每小题3分,满分30分)
1.用科学记数法表示62500的结果是 。
2、顺次连结任意四边形各边中点所得的四边形是__________;
3、函数![]() 中,自变量x的取值范围是__________;
中,自变量x的取值范围是__________;
4、不等式组![]() 的整数解是______ ____;
的整数解是______ ____;
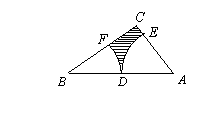 5、分解因式:
5、分解因式:![]() .
.
6、直角三角形的两边长为5,12,则其外接圆半径是 .
7、已知点P(m,2)与点Q(3,n)关于原点对称,则m= ;n=
8、如图,直角![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,分别以
的中点,分别以
点A、B为圆心,AD长为半径作弧,分别交AC、BC于点E、F,则图中阴影部分面积是 .
9、一个抛物线开口向上,其顶点坐标是(2,3),试写出符合要求的抛物线解析式___________(填写一个即可)。
10、从鱼塘捕得同时放养的草鱼240尾,从中任选9尾,称得每尾鱼的质量分别是1.5,1.6,1.4,1.6,1.3,1.4,1.2,1.7,1.8(单位:千克).依此估计这240尾鱼的总质量大约是 。
二、选择题(本题共5小题,每小题3分,满分15分)
11、下列计算正确的是( )
A.a2+a2=2a4 B.a6÷a3=a2
C.(-a3)2=-a6 D.a3·a2=a5
12、下列二次根式中,最简二次根式是( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
13、下列图形既不是轴对称图形也不是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.菱形 D.直角梯形
14、两圆的半径长分别为4和6,圆心距为2,那么这两个圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
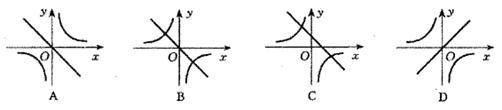 15、函数y=kx与y=
15、函数y=kx与y=![]() (k≠0)在同一坐标系中的图象大致是( )
(k≠0)在同一坐标系中的图象大致是( )
三、解答题(每小题6分,满分24分)
16.解不等式组,并在数轴上表示出解集:
![]() 3x+5>-2x …………………①
3x+5>-2x …………………①
x+4 ≥2x-1 …………②
17.若关于x的方程x2-mx+2=0与x2-(m+1)x+m=0有一个相同的实数根,求m的值和相同的实数根.
 |
18.有一块三角形的地,现要平均分给四农户种植(即四等分三角
形面积).请你在图中上作出分法. (不写作法,保留作图痕迹)
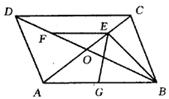 19、如图,在□ABCD中,对角线AC、BD相交于O点,BD=2AD,E、F、G分别是OC、OD、AB的中点.求证:EG=EF.
19、如图,在□ABCD中,对角线AC、BD相交于O点,BD=2AD,E、F、G分别是OC、OD、AB的中点.求证:EG=EF.
四、本大题共4小题,20~21小题各7分,22~23小题各8分,满分30分。
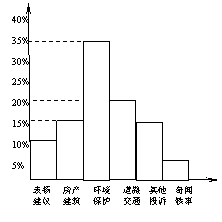 20.如图,是一个城市某晚报“百姓热线”一周内接到的热线电话的统计图,其中有关环境保护问题有70个,请回答下列问题:
20.如图,是一个城市某晚报“百姓热线”一周内接到的热线电话的统计图,其中有关环境保护问题有70个,请回答下列问题:
(1)本周“百姓热线”共接到热线电话多少个?
(2)你对这个城市的看法如何?用自己的话简要地概括出来。
21.某学校要向山区同学捐赠3500册图书,实际共捐赠了4125册,其中初中学生捐赠了原计划的120%,高中学生捐赠了原计划的115%.问初中学生和高中学生分别比原计划多捐赠多少册.
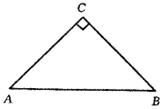 22.如图,AB是等腰直角三角形ABC的斜边.若点M在AC上,点N中BC上,以直线MN为轴将△MCN翻折,使点C落在AB上,设其落点为P(不与A、B重合).
22.如图,AB是等腰直角三角形ABC的斜边.若点M在AC上,点N中BC上,以直线MN为轴将△MCN翻折,使点C落在AB上,设其落点为P(不与A、B重合).
(1)当点P是AB的中点时,求证:PA∶PB=CM∶CN;
(2)当点P不是AB的中点时,PA∶PB=CM∶CN是否仍然成立?请证明你的结论.
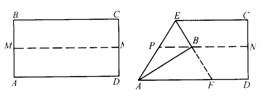
23.如图,先把矩形纸片ABCD对折, 折痕为MN,恢复原状后,再把点B叠折到折痕MN上(如图),设EB的延长线交AD于F试判断AEF的形状,并说明理由。
五、本题共2小题,其中24题10分,25题11分
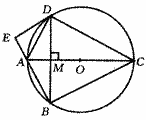 24.已知:如图,四边形ABCD内接于⊙O,AC为⊙O的直径,弦DB⊥AC,垂足为M,过点D作⊙O的切线,交BA的延长线于点E.若AC=10,tan∠DAE=
24.已知:如图,四边形ABCD内接于⊙O,AC为⊙O的直径,弦DB⊥AC,垂足为M,过点D作⊙O的切线,交BA的延长线于点E.若AC=10,tan∠DAE=![]() ,求DB和DE的长.
,求DB和DE的长.
25.本题各小题均不必证明.
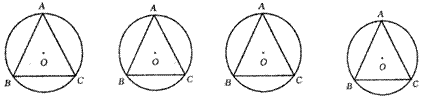 如图1,一个圆形街心花园,有三个出口A、B、C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一个亭子.为使亭子与原有的道路相通,需再修三条小路OD、OE、OF,使出口D、E、F分别落在△ABC的三边上,且这三条小路把△ABC分成三个全等的多边形,以备种植不同品种的花草.
如图1,一个圆形街心花园,有三个出口A、B、C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一个亭子.为使亭子与原有的道路相通,需再修三条小路OD、OE、OF,使出口D、E、F分别落在△ABC的三边上,且这三条小路把△ABC分成三个全等的多边形,以备种植不同品种的花草.
图1 图2 图3 图4
(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1、图2中.
(2)要使三条小路把△ABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长;
(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法(图4供你探究时使用);