九年级数学中考模拟试题(华师大)
一、选择题(每小题4分,共40分)
1、下列各组数中,互为相反数的是( )
A、3与 B、-1与![]() C、
C、![]() 与-1 D、3与│-3│
与-1 D、3与│-3│
2、下列各式与![]() 相等的是(
)
相等的是(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、下列运算正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知M是⊙O内一点,过M点的⊙O的最长弦为10㎝,最短弦为8㎝,则OM的长度是( )
A、2㎝ B、5㎝ C、4㎝ D、3㎝
5、在下面四种正多边形中用同一种图形不能平面镶嵌的是( )
A、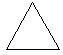 B、
B、 C、
C、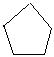 D、
D、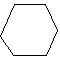
6、已知a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数y=x2图像上,则( )
A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y1<y3
7、螺旋藻是一种营养特别丰富的保健品,已知1克的螺旋藻相当于1000克蔬菜营养的综合,那没么3吨重的螺旋藻相当于( )千克蔬菜营养的综合。
A、3×![]() B、3×
B、3×![]() C、3×
C、3×![]() D、3×
D、3× ![]()
8、如图,是正方体表面展开图,如果将其合成原来的正方体时,与点P重合的两点应是( )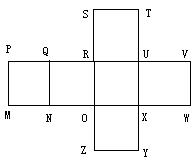
A、S和E B、T和Y C、V和Y D、T和V
9、一个袋中装有两个黄球和两个红球,任意摸出一个球后放回,再任意摸出一个球,则两次都摸到红球的机会大小是( )
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
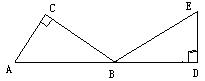 10、如图在Rt△ABC中,∠C=60°,AC=
10、如图在Rt△ABC中,∠C=60°,AC=![]() ㎝,将△ABC绕点B旋转至△BDE位置,且使点A、B、D三点在同一直线上,则点A经过的最短路线长度是( )
㎝,将△ABC绕点B旋转至△BDE位置,且使点A、B、D三点在同一直线上,则点A经过的最短路线长度是( )
A、![]() ㎝ B、
㎝ B、![]() ㎝ C、
㎝ C、![]() ㎝ D、
㎝ D、![]() ㎝
㎝
二、填空题(每题4分,共20分)
11、分解因式:![]() 。
。
12、等腰△ABC中,已知∠A=40°,则另两角大小是 。
 13、观察一列数:3,8,13,18,23,……依此规律,在此数列中比2005大的最小整数是 。
13、观察一列数:3,8,13,18,23,……依此规律,在此数列中比2005大的最小整数是 。
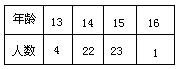
14、某班50名学生的年龄统计结果如右表所示:这个班学生年龄的众数是 ,中位数是 。
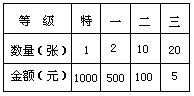
15、一家商店搞促销活动,发奖券一万张,每购100元物品,得奖券1张。设奖情况如右表,结果一位顾客购物后得到1张奖券,那么他获奖的机会是
。
三、(每小题8分,共16分)
16、当![]() 时,求代数式
时,求代数式![]() 的值。
的值。
17、若方程组![]() 的解满足x+y>0,求m的取值范围。
的解满足x+y>0,求m的取值范围。
四、(每小题8分,共16分)
18、已知![]() 的值。
的值。
19、已知:如图,正方形ABCD中,AC与BD相交于O点,E、F分别是DB、BD延长线上一点,且BE=DF。试说明:∠E=∠F。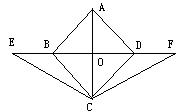
五、(每题10分,共20分)
20、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同。随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元(不足100元不返券)。他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
21、货轮以每小时40海里的速度沿南偏东30°方向航行,在B处观测灯塔A位于南偏东75°方向上,货轮航行半小时后到达C处,观测灯塔A位于北偏东60°方向上。画图并求出货轮到达C处与灯塔A的距离。
六、(满分12分)
22、某同学想计算出15°角的三角函数值,利用平面几何的知识设计了一种图形(如图所示):△ABC中,∠C=90°,∠ABC=30°,延长CB至D使BD=AB,连结AD。请你根据该同学设计的图形计算出15°角的正切值。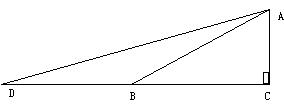
七、(满分12分)
23、为了了解学生的身高情况,抽测了某校17岁50名男生的身高,数据如下(单位:米)
| 身高 | 1.57 | 1.59 | 1.60 | 1.62 | 1.63 | 1.64 | 1.65 | 1.66 | 1.68 |
| 人数 | 1 | 1 | 2 | 2 | 3 | 2 | 1 | 6 | 5 |
| 身高 | 1.69 | 1.70 | 1.71 | 1.72 | 1.73 | 1.74 | 1.75 | 1.76 | 1.77 |
| 人数 | 8 | 7 | 2 | 3 | 2 | 1 | 2 | 1 | 1 |
若将数据分成7组,取组距为0.03米。相应的频率分布表是:
| 分组 | 频数 |
| 1.565~1.595 | 2 |
| 1.595~1.625 | 4 |
| 1.625~1.655 | 6 |
| 1.655~1.685 | 11 |
| 1.685~1.715 | 17 |
| 1.715~1.745 | 6 |
| 1.745~1.775 | 4 |
| 合计 | 50 |
(1) 样本数据中,17岁男生身高的众数、中位数分别是多少?
(2) 依据样本数据,估计这所学校17岁的男生中,身高不低于1.65米且不高于1.70米的学生所占的百分比?
(3) 观察频数分布表,指出该校17岁的男生中,身高在哪个数据范围内的频数最大。如果该校17岁的男生共有350人,那么在这个身高范围内的人数估计有多少人?
八、(本题满分14分)
24、如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答下列问题:
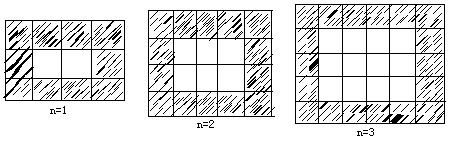
(1)在第n个图中,每一行共有 块瓷砖,每一竖列共有 块瓷砖。(均用含n的代数式表示);
(2)设铺设地面所用的瓷砖的总块数为y,请写出y与(1)中的n的函数关系式(不要求写自变量n的取值范围);
(3)按上述铺设方案,铺一块这样的矩形地面共用506块瓷砖,求此时n的值;
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明。