《线段、角》基础测试

《线段、角》基础测试

（时间90分）

一、判断题（每小题1分共8分，对的在括号内画“√”，错的画“×”）．

1．经过三点中的每两个，共可以画三条直线…………………………………（　　）

【提示】

平面内三点可以在同一条直线上，也可以不在同一条直线上．

【答案】

×．

【点评】

要注意，三个点的相互位置共有两种情况，如图

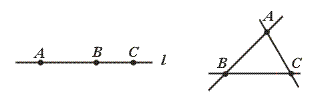
（1）　　　　　　　　　　（2）

因此，平面内经过三点中每两个的直线可以是同一条，也可以是三条，必须把上面两种情况全部考虑到，再分类解决，若只考虑其中的第二种情况，判断就会出错．

2．射线AP和射线PA是同一条射线………………………………………………（　　）

【提示】

表示射线端点的字母要写在前，另一个字母写在后，端点不同的射线不是同一条射线．

【答案】

×．

3．连结两点的线段，叫做这两点间的距离…………………………………………（　　）

【提示】

连结两点的线段的长度，叫做这两点的距离．

【答案】

×．

【点评】

“线段”表示的是“图形”，而“距离”指的是线段的“长度”，指的是一个“数”，两者不能等同．

4．两条直相交，只有一个交点……………………………………………………（　　）

【提示】

两条不同的直线，如果它们有一个公共点，我们就说它们相交，若两条直线相交，有两个公共点，那么根据直线公理：经过两点有且只有一条直线，则这两条直线实际上是同一条直线了．同样两条不同的直线不能有三个或更多的公共点．

【答案】

√．

5．两条射线组成的图形叫做角……………………………………………………（　　）

【提示】

有公共端点的两条射线组成的图形叫做角．

【答案】

×．

【点评】

“角”的构成有两个条件：①有公共端点；②两条射线组成的图形．两者缺一不可，按题中的叙述，可以画出这样的图形（如下图），显然这个图形不是角．

6．角的边的长短，决定了角的大小．

【提示】

角的大小，与组成角的两条射线张开的程度相关，或者说与射线绕着它的端点旋转过的平面部分的大小相关，与角的边画出部分的长短无关．

【答案】

×．

【点评】

我们在现实生活中看到的直线或射线，其实大多数以线段的形式出现的，所以在运用直线或射线概念时，千万别忘了它们的几何意义，否则就要出错．

7．互余且相等的两个角都是45°的角…………………………………………（　　）

【提示】

“互余”即两角和为90°．

【答案】

√．

【点评】

设相等的两个角为x°，由“互余”得，2x＝90，∴ x＝45（度），以正确的计算为依据，也是作判断题的方法之一．注意，角度是一个带单位的数．设未知数时，未知量带单位，则列式中即可不用带单位．这与解其他类型的应用题格式相同．

8．若两个角互补，则其中一定有一个角是钝角……………………………………（　　）

【提示】

“互补”即两角和为180°．想一想：这里的两个角可能是怎样的两个角？

【答案】

×．

【点评】

两角互补，这里的两角有两种情形，如图：

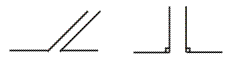
图（1）　　　　　 图（2）

因此，互补的两个角中，可能有一个是钝角，也可能两个角都是直角，因此在作出判断前必须全面地考虑，这就要求有“分类讨论”的思想，“分类讨论”是数学中重要的思想方法之一．

二、填空题（每空1分，共28分）

1．过平面内的三个点中的每两个画直线，最少可画____条直线，最多可画_____条直线．

【提示】

分三点在一条直线上和三点不在同一条直线上两种情况．

【答案】

1，3．

2．如图，线段AB上有C、D、E、F四个点，则图中共有_____条线段．

【提示】

方法一：可先把点A作为一个端点，点C、D、E、F、B分别为另一个端点构成线段，再把点C作为一个端点，点D、E、F、B分别为另一个端点构成线段……依此类推，数出所有线段求和，即得结果．

方法二：先数出相邻两点间线段的条数，再数出中间隔一点或隔二点、或隔三点……数出各种情况线段的条数，将它们相加，即得结果．

【答案】

15．

【点评】

一条线段上有4个点，则共有5＋4＋3＋2＋1条线段；若线段上再增加一个点，即有5个点，则共有6＋5＋4＋3＋2＋1条线段；若一条线段上有n个点呢？则有(n＋1)＋n＋(n－1)＋…＋3＋2＋1＝条线段，每增加一个点，就增加(n＋1)条线段．

3．线段AB＝6 cm，BC＝4 cm，则线段AC的长是______．

【提示】

分点C在AB的延长线上或点C在AB上两种情形．

【答案】

10 cm或2 cm．

【点评】

（1）当点C在AB延长线上时，如图，则AC＝AB＋BC＝6＋4＝10（cm）；

（2）当点C在AB上时，如图，则AC＝AC－BC＝6－4＝2（cm），点有位置不同，故应有两种情形．

4．把线段AB延长到点C，使BC＝AB，再延长BA到点D，使AD＝2AB，

则DC＝_____AB＝____AC；BD＝_____AB＝_____DC．

【提示】

根据题意，画出符合条件的图形，如图，答案是否明白了？

【答案】

4，2；3，．

【点评】

判断线段间的数量关系，应画出符合题意的图形，结合图形正确分析方能得出正确的结论，这里要注意“延长线段AB”与“延长线段BA”的区别．

5．45°＝______直角＝_____平角＝____周角．

【提示】

1直角＝90°，且1直角＝平角＝周角．

【答案】

，，．

6．18.26°＝___°___′___″；12°36′18″______°．

【提示】

1°＝60′，1′＝60″，高一级单位化成低一级单位，用乘法，乘以60；低一级单位化成高一级单位，用除法，除以60．

【答案】

18，15，36；12.605．

7．只有_____角有余角，而且它的余角是_____角．

【提示】

①互余的两角和为90°；

②0°＜锐角＜90°．

【答案】

锐、锐．

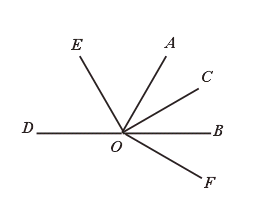
8．如图，∠AOC＝∠COE＝∠BOD＝90°，则图中与∠BOC相等的角为_____；

与∠BOC互余的角为______，与∠BOC互补的角为______．

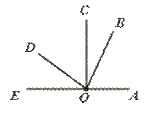
【提示】

互余的两角和为90°，互补的两角和为180°；同角或等角的余角相等，同角或等角的补角相等．

【答案】

∠DOE，∠AOB、∠COD；∠AOD．

【点评】

互补两角，图形上并非一定出现相邻两角为平角，而只要求和为180°，类似地，也应这样去理解互为余角的概念．

9．∠a 与它的余角相等，∠b与它的补角相等，则∠a＋∠b＝____°．

【提示】

互余且相等的角是45°，互补且相等的角是90°．

【答案】

135°．

10．互为余角两角之差是35°，则较大角的补角是_____°．

【提示】

先根据互余两角和为90°，差是35°，求出较大角，然后再求较大角的补角．

【答案】

117.5°．

【点评】

设互余两角为a，b，且a＞b，则．解这个方程组，即可求出∠a的度数，这种和用方程组解决几何计算题的方法以后还会经常用到．

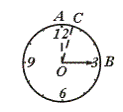
11．钟表在12时15分时刻的时针与分针所成的角是_____°．

【提示】

钟面上时针每小时旋转1大格为30°，则每分旋转0.5°；分针每小时旋转12大格为

360°，则每分转6°．

【答案】

如图，∠BOC＝∠AOB－∠AOC

＝30°×3－0.5°×15

＝90°－7.5°

＝82.5°

12．用定义、性质填空：

（1）如下图，

∵ M是AB的中点，

∴ AM＝MB＝AB．（　　　　　　　　　　）

（2）如下图，

∵ OP是∠MON的平分线，

∴ ∠MOP＝∠NOP＝∠MON．（　　　　　　　　　　　　  ）

（3）如下图，

∵ 点A、B、C在一条直线上，

∴ ∠ABC是平角（　　　　　　　　　　　　  ）

（4）如下图，

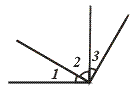
∵ ∠1＋∠2＝90°，∠3＋∠2＝90°，

∴ ∠1＝∠3（　　　　　　　　　　　　　  ）

【提示】

根据线段中点、角平分线概念、互为余角的性质填写．

【答案】

线段中点的定义，角平分线的定义，平角的定义，同角的余角相等．

【点评】

定义性质是推理的依据，要学会定义、性质的符号表达式，为后面的进一步学习做好准备．

三、选择题（每小题2分，共16分）

1．如图，B、C、D是射线AM上的一个点，则图中的射线有………………（　　）

（A）6条　 （B）5条　　（C）4条　　 （D）1条

【提示】

射线是指直线上一点和它一旁的部分，射线有一个端点，可以向一方无限延伸．

【答案】

B．

2．下列四组图形（其中AB是直线，CD是射线，MN是线段）中，能相交的一组是（　　）

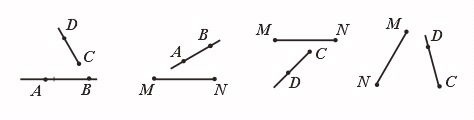
（A）　　　　 （B）　　　　 （C）　　　　　 （D）

【提示】

直线没有端点，可以向两方无限延伸；射线有一个端点，可以向一方无限延伸；线段有两个端点，题中四组图形，画出部分都没相交、要找出能相交的一组，就看直线、射线可延伸出部分能否与另一条线相交．

【答案】

B．

3．如图，由AB＝CD，可得AC与BD的大小关系是…………………………（　　）

（A）AC＞BD　　（B）AC＜BD　　（C）AC＝BD　　 （D）不能确定

【提示】

由AB＝CD，两边同时减去CB，即可找出答案．

【答案】

C．

4．如图，M是线段AB的中点，N是线段AB上一点，AB＝2a，NB＝b，下列说法中

错误的是…………………………………………………………………………（　　）

（A）AM＝a　　（B）AN＝2a－b　　（C）MN＝a－b　　（D）MN＝a

【提示】

由“M是线段AB的中点，AB＝2a”，可得AM＝MB＝AB＝a．

【答案】

D．

5．下列说法中正确的是…………………………………………………………（　　）

（A）角是由一条射线旋转而成的

（B）角的两边可以度量

（C）一条直线就是一个平角

（D）平角的两边可以看成一条直线

【提示】

角是由一条射线绕着它的端点旋转而成的图形，角的边是射线，角有顶点．

【答案】

D．

【点评】

平角的两边互为反向延长线，可以构成一条直线，但不可把直线当作直角，因为直线没有明确角的顶点．

6．下列四个图形中，能用∠，∠O，∠AOB三种方式正确表示同一个角的图形是（　　）

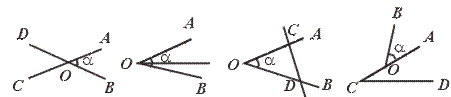
（A）　　　　　　　　 （B）　　　　　  （C）　　　　　　　 （D）

【提示】

当且仅当顶点处只有一个角时，可用顶点的大写字母表示这个角．

【答案】

C．

7．如图，∠AOB是一直角，∠AOC＝40°，OD平分∠BOC，则∠AOD等于（　　）

（A）65°　 （B）50°　 （C）40°　　（D）25°

【提示】

∠AOD＝∠AOB－∠BOD或者∠AOD＝∠AOC＋∠COD．

【答案】

A．

【点评】

观察图形，确定角与角之间的关系是解决此题的关键．

8．下列说法中正确的是…………………………………………………………（　　）

（A）一个角的补角一定比这个角大

（B）一个锐角的补角是锐角

（C）一个直角的补角是直角

（D）一个锐角和一个钝角一定互为补角

【提示】

0°＜锐角＜90°，1直角＝90°，90°＜钝角＜180°，互补两角的和是180°．

【答案】

C．

四、计算（每小题2分，共8分）

1．37°28′＋44°49′；　　2．108°18′－52°30″；

3．25°36′×4；　　　　　 4．40°40′÷3．

【提示】

1°＝60′，1′＝60″，低一级单位满“60”，要向高一级单位进“1”，由高一级单位借“1”要化成“60”加入低一级单位参与运算．

【答案】

1．82°17′；　2．56°17′30″；　3．102°24′；　 4．13°33′20″．

五、画图题（共15分）

1．（４分）读句画图：如图，A、B、C、D在同一平面内．

（1）过点A和点D画直线；

（2）画射线CD；

（3）连结AB；

（4）连结BC，并反向延长BC．

【答案】

如图：

【点评】

画直线AD时，要画出向两方延伸的情况，画射线CD时，要画出向D的一旁延伸的情况，画线段AB时，则不要画出向任何一旁延伸的情况，线段是射线、直线的一部分，射线又是直线的一部分．

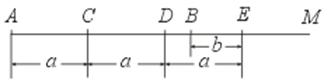
2．（４分）已知线段a、b（如图），画出线段AB，设AB＝3a－b，并写出画法．

【答案】

方法一：

①量得a＝1.9 cm，b＝2.6 cm；

②算AB的长，AB＝3×1.9－×2.6＝4.4（cm）；

③画线段AB＝4.4 cm．

则线段AB就是所要画的线段．

方法二：

①画射线AM，并在射线AM上顺次截取AC＝CD＝DE＝a；

②在线段EA上截取EB＝b．

则线段AB就是要画的线段．

【点评】

①写画法就是按照画图的顺序，交代清楚在什么位置（在射线AM上）上画什么样的线段，怎样画（顺次截取），哪一条线段就是要画的线段．

②涉及到的概念用语（是射线还是线段），位置术语（在……上），动作术语（截取还是顺次截取）等都要仔细体会，正确运用．

3．（４分）用三角板画15°与135°的角．

【提示】

15°＝45°－30°＝60°－45°；135°＝90°＋45°＝180°－45°．

【答案】

如图：

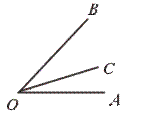或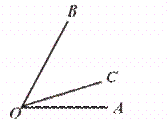　　　

则∠AOC就是所要画的15°角．

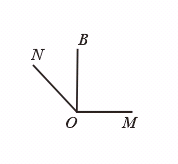或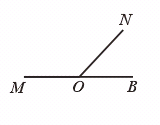　

则∠MON就是所要画的135°的角．

4．（3分）已知：∠1与∠2，且∠1＞∠2，画∠AOB，使∠AOB＝（∠1－∠2）．

【答案】

方法一

①量得∠1＝120°，∠2＝44°；

②算∠AOB＝(120°－44°)＝38°；

③画∠AOB＝38°．

则∠AOB就是所要画的38°角．

方法二

①画∠AOC＝120°；

②以O为顶点OC为一边在∠AOC的内部画∠COD＝44°；

③量得∠AOD＝76°，则∠AOD＝38°；

④以O为顶点，OA为一边，在∠AOD的内部画∠AOB＝38°．

则∠AOB就是所要画的38°的角．

【点评】

无论方法一还是方法二，都要使用量器画角，有一定的局限性，常常会有误差．以后，我们还要学习“尺规作图”的方法，从而能提高画图能力．

5．读句画图填空（每空1分，共10分）

（1）画∠AOB＝60°．

（2）画∠AOB的平分线OC，则∠BOC＝∠____＝∠____＝____°．

（3）画OB的反向延长线OD，则∠AOD＝∠____－∠AOB＝_____°．

（4）画∠AOD的平分线OE，则∠AOE＝∠____＝_____°，∠COE＝_____°．

（5）以O为顶点，OB为一边作∠AOB的余角∠BOF，则∠EOF＝____°，射线OC、OB将∠____三等分．

【答案】

（2）AOC、AOB、30；（3）BOD、120；（4）DOE、60，90；（5）150，AOF．

【点评】

读句画图，看图填空，把几何图形与语句表示，符号书写融为一体，看到了图形形成的过程，利于识图．

六、解答题（每小题5分，共15分）

1．如图，M是线段AB的中点，点C在线段AB上，且AC＝4 cm，N是AC的中点，

MN＝3 cm，求线段CM和AB的长．

【提示】

CM＝MN－NC，AB＝2 AM．

【答案】

∵ N是AC中点，AC＝4 cm，

∴ NC＝AC＝×4＝2（cm），

∵ MN＝3 cm，

∴ CM＝MN－NC＝3－2＝1（cm），

∴ AM＝AC＋CM＝4＋1＝5（cm），

∵ M是AB的中点，

∴ AB＝2 AM＝2×5＝10（cm）．

答：线段CM的长为1 cm，AB的长为10 cm．

【点评】

在进行线段的有关计算时，要依据已知，仔细看图，找出已知线段与所求线段的关系，关于线段中点的三种表达方式，应结合图形灵活运用．

2．已知∠a与∠b 互为补角，且∠b 互为补角，且∠b 的比∠a大15°，求∠a的余角．

【提示】

互补两角和为180°，根据题意可知列出关于∠a、∠b的方程组，求出∠a，再根据“互余两角和为90°”，求出∠a的余角．

【答案】

由题意可得：

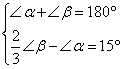
解之得：

∴ ∠a的余角＝90°－∠a＝90°－63°＝27°．

答：∠a的余角是27°．

3．如图，∠AOB是直角，∠AOC等于46°，OM平分∠AOC，ON平分∠BOC，求∠MON的度数．

【提示】

∠MON＝∠CON－∠COM．

【答案】

∵　∠AOB是直角．

∴　∠AOB＝90°（直角的定义），

∵　∠AOC＝46°，

∴　∠BOC＝∠AOB＋∠AOC＝90°＋46°＝136°，

∵　ON平分∠BOC，

∴  ∠CON＝∠BOC＝×136°＝68°（角平分线定义），

∵　OM平分∠AOC，

∴　∠COM＝∠AOC＝×46°＝23°（角平分线定义），

∴　∠MON＝∠CON－∠COM＝68°－23°＝45°．

答：∠MON＝45°．

【点评】

和线段计算一样，在进行有关角度计算时，也要根据已知，仔细看图，找出已知角与所求角的关系，此题中的∠MON还可看成是∠BOM与∠BON的差，∠MON也可看成是∠AOM与∠AON之和，请试一试怎么算，比一比哪种方法较简便．关于角平分线的三种表达式，也应结合图形灵活运用．