《相似形》基础测试
（一）选择题：（每题2分，共24分）
1．已知5y－4x＝0，那么（x＋y）︰（x－y）的值等于………………………………（ ）
（A）
（B）－9 （C）9 （D）－
【提示】将5y－4x＝0改写成
＝
，用比例性质得
＝
．【答案】C．
【点评】本题要求运用比例性质进行计算．
2．已知线段d是线段a、b、c的第四比例项，其中a＝2 cm，b＝4 cm，c＝5 cm，则d等于……（ ）
（A）1 cm（B）10 cm（C）
cm（D）
cm．
【提示】列出比例式：a︰b＝c︰d，解出d．【答案】B．
【点评】本题要求运用比例的概念和求第四比例项的基本方法．
3．如图，DE∥BC，在下列比例式中，不能成立的是………………………………（ ）
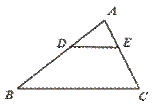
（A）
＝
（B）
＝ （C）
＝
（D）
＝
【提示】用特殊值法来筛选出选项，D、E分别为AB、AC的中点，计算每个线段比．【答案】B．
【点评】本题要求运用平行线分线段成比例定理和三角形一边平行线的性质定理，选B的原因是，当E为AC的中点时，
＝1，D为AB的中点，
＝
．
4．下列判断中，正确的是………………………………………………………………（ ）
（A）各有一个角是67°的两个等腰三角形相似
（B）邻边之比都为2︰1的两个等腰三角形相似
（C）各有一个角是45°的两个等腰三角形相似
（D）邻边之比都为2︰3的两个等腰三角形相似
【提示】设计出反例淘汰错误的选项．【答案】B．
【点评】本题要求运用相似三角形的判定定理．A不成立的原因是当底角为67°时，顶角为46°，另一个三角形的顶角为67°时，底角为66.5°，这两个等腰三角形不相似．C不成立的原因也是顶角不等．D不成立的原因是当一个等腰三角形的腰与底的比是2︰3时，另一个等腰三角形的腰与底的比为3︰2，它们三边之比分别为2︰2︰3与3︰3︰2．
5．如图，在Rt△ABC中，CD是斜边AB上的高，则图中的相似三角形共有………（ ）
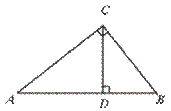
（A）1对 （B）2对 （C）3对 （D）4对
【提示】考虑Rt△ABC与Rt△ACD和Rt△CBD相似情况．
【答案】C．
【点评】本题要求运用直角三角形被斜边上的高所分割成两个直角三角形这种基本图形．
6．已知：如图，∠ADE＝∠ACD＝∠ABC，图中相似三角形共有………………（ ）
（A）1对 （B）2对 （C）3对 （D）4对
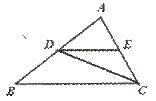
【提示】分别把CD、DE擦去，考察△ADE和△ABC、△ACD和△ABC的关系．【答案】C．
【点评】本题要求运用三角形相似的基本定理与判定定理的运用．
7．如图，□ABCD中，E是AD延长线上一点，BE交AC于点F，交DC于点G，则下列结论中错误的是…………………………………………………………………（ ）
（A）△ABE∽△DGE （B）△CGB∽△DGE
（C）△BCF∽△EAF （D）△ACD∽△GCF
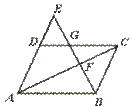
【提示】考察两个三角形中是否有对应边互相平行．【答案】D．
【点评】本题要求运用三角形相似的基本定理．
8．如图，在△ABC中，D为AC边上一点，∠DBC＝∠A，BC＝
，AC＝3，则CD的长为…………………………………………………（ ）
（A）1 （B）
（C）2 （D）
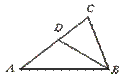
【提示】由△ABC∽△BDC，列出对应边的比例式．【答案】C．
【点评】本题要求运用相似三角形的判定定理与性质定理．
9．如图，D是△ABC的边AB上一点，在条件（1）∠ACD＝∠B，（2）AC2＝AD·AB，（3）AB边上与点C距离相等的点D有两个，（4）∠B＝∠ACB中，一定使
△ABC∽△ACD的个数是………………………………………………………（ ）
（A）1 （B）2 （C）3 （D）4
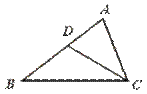
【提示】由于∠A为公共角，所以考虑另一个对应角相等或∠A的两边对应成比例，才能有△ABC∽△ACD．【答案】B．
【点评】本题要求运用相似三角形的判定定理．题中条件（4），∠B与∠ACB都不是
△ACD的内角，不可能成为△ABC和△ACD的对应角．由下图可见，条件（3）不一定能使△ABC∽△ACD．
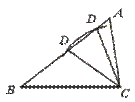
10．如图，在Rt△ABC中，∠C＝90°，CD⊥AB于D，且AD︰BD＝9︰4，则
AC︰BC的值为………………………………………………………………（ ）
（A）9︰4 （B）9︰2 （C）3︰4 （D）3︰2
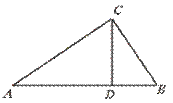
【提示】先设AD＝9k，BD＝4k，求出CD或AB，再求出AC和BC．【答案】D．
【点评】本题要求运用直角三角形被斜边上的高分成两个三角形与原三角形相似的定理．也可利用射影定理，由
，
，得
．
11．如图，点A1、A2，B1、B2，C1、C2分别是△ABC的边BC、CA、AB的三等分点，且ABC的周长为l，则六边形A1A2B1B2C1C2的周长为…………………………（ ）
（A）
l （B）3l （C）2l （D）l
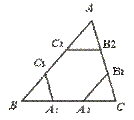
【提示】C1B2＝A1A2＝BC，B1A2＝C1C2＝AB，A1C2＝B1B2＝AC．【答案】D．
【点评】本题要求运用相似三角形的周长比等于相似比（即 对应边的比）．
12．如图，将△ABC的高AD四等分，过每一个分点作底边的平行线，把三角形的面积分成四部分S1、S2、S3、S4，则S1︰S2︰S3︰S4等于……………………………（ ）
（A）1︰2︰3︰4 （B）2︰3︰4︰5 （C）1︰3︰5︰7 （D）3︰5︰7︰9
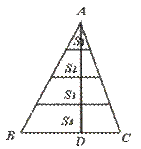
【提示】
＝（
）2，
＝（
）2．
【答案】C．
【点评】本题要求运用相似三角形的面积比等于相似比的平方（即对应边上的高的比的平方）．
（二）填空题：（每题2分，共20分）
13．如果x︰y︰z＝1︰3︰5，那么
＝___________．
【提示】取x＝1，y＝3，z＝5代入，或设x＝k，则y＝3k，z＝5k．
【答案】－
．
【点评】本题要求运用比例性质求值．
14．已知数3、6，再写出一个数，使这三个数中的一个数是另外两个数的比例中项，这个数是___________（只需填写一个数）．
【提示】将b2＝ac中任意两个字母用3、6代替，求出第三个字母所表示的数．
【答案】±12或±3
或±．
【点评】本题要求运用比例的有关概念．它是一道开放性问题，用数3、5、6代替不同字母，答数也就不同．
15．如图，l1∥l2∥l3，BC＝3，
＝2，则AB＝___________．
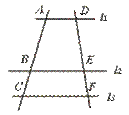
【提示】
＝
．
【答案】6．
【点评】本题要求运用平行线分线段成比例定理．
16．如图，已知DE∥BC，且BF∥EF＝4︰3，则AC︰AE＝__________．
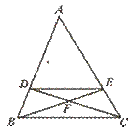
【提示】△BCF∽△EDF和△ABC∽△ADE构成两种基本图形.
【答案】4︰3．
【点评】本题要求运用三角形一边平行线的性质定理．
17．如图，在△ABC中，∠BAC＝90°，D是BC中点，AE⊥AD交CB延长线于点E，则△BAE相似于______．
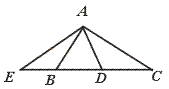
【提示】∠BAE＝∠DAC＝∠C．
【答案】△ACE．
【点评】本题要求灵活运用三角形相似的判定定理．
18．如图，在矩形ABCD中，E是BC中点，且DE⊥AC，则CD︰AD＝__________．
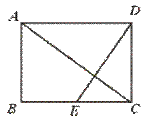
【提示】Rt△CDE∽Rt△DCA，并设AD为a，用a表示出EC和CD的长，或
．
【答案】
．
【点评】本题要求运用直角三角形的判定定理．
19．如图∠CAB＝∠BCD，AD＝2，BD＝4，则BC＝__________．
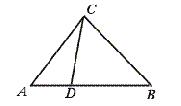
【提示】由△ABC∽△CBD，得BC2＝BD·AB．
【答案】2．
【点评】本题要求运用相似三角形的判定定理与性质．
20．如图，在△ABC中，AB＝15 cm，AC＝12 cm，AD是∠BAC的外角平分线，
DE∥AB交AC的延长线于点E，那么CE＝__________cm．
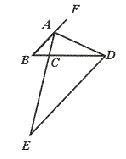
【提示】∠EAD＝∠FAD＝∠ADE，
∴ ED＝AE＝AC＋CE．
再利用△ABC∽△EDC．
【答案】48．
【点评】本题要求灵活运用相似三角形的判定定理和性质．
21．如图，在△ABC中，M、N是AB、BC的中点，AN、CM交于点O，那么
△MON∽△AOC面积的比是____________．
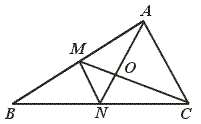
【提示】利用三角形中位线定理．
【答案】1︰4．
【点评】本题要求运用相似三角形的判定、相似三角形的面积比等于相似比的平方，以及三角形的中位线定理．
22．如图，在正方形ABCD中，F是AD的中点，BF与AC交于点G，则△BGC与四边形CGFD的面积之比是_____________．
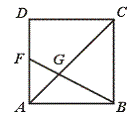
【提示】△BGC∽△FGA，推出FG＝
BG，得连结FC．S△BCF＝S正方形，再列出
S△CDF与S正方形的关系式．或由△BGC∽△FGA得
，所以
S△AFG＝
S△BCG＝S△AGB，又 S△ACD＝S△ACB，从而得出S四边形CGFD＝5S△AFG，
S△BCG＝4S△AFG．
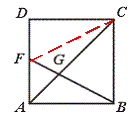
【答案】4︰5．
【点评】本题要求运用相似三角形的基本定理与性质．
（三）计算题（每题6分，共24分）
23．如图，DE∥BC，DF∥AC，AD＝4 cm，BD＝8 cm，DE＝5 cm，求线段BF的长．
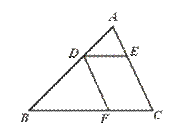
【提示】先求出FC．
【答案】∵ DE∥BC，DF∥AC，
∴ 四边形DECF是平行四边形．
∴ FC＝DE＝5 cm．
∵ DF∥AC，
∴ 
＝
．
即 
＝
，
∴ BF＝10（cm）．
【点评】本题要求运用平行四边形判定定理和性质定理、平行线分线段成比例定理．
24．如图，已知△ABC中，AE︰EB＝1︰3，BD︰DC＝2︰1，AD与CE相交于F，求
＋
的值．
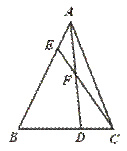
【提示】作EG∥BC交AD于G．
【答案】作EG∥BC交AD于G，则由
＝，即
＝，得
EG＝BD＝CD，
∴ ＝
＝．
作DH∥BC交CE于H，则DH＝BE＝AE．
∴ ＝
＝1，
∴ ＋＝＋1＝．
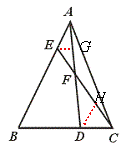
【点评】本题要求灵活运用三角形一边平行线的性质定理．
25．如图，点C、D在线段AB上，△PCD是等边三角形．
（1）当AC、CD、DB满足怎样的关系时，△ACP∽△PDB？
（2）当△ACP∽△PDB时，求∠APB的度数．
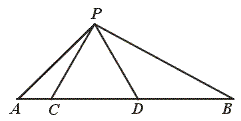
【提示】（1）考虑AC、PD、PC、DB之间比例关系．
（2）利用相似三角形的性质“对应角相等”．
【答案】∵ ∠ACP＝∠PDB＝120°，
当
＝
，即
＝
，也就是CD2＝AC·DB时，△ACP∽△PDB．
∴ ∠A＝∠DPB．
∴ ∠APB＝∠APC＋∠CPD＋∠DPB
＝∠APC＋∠A＋∠CPD
＝∠PCD＋∠CPD
＝120°．
【点评】本题要求运用相似三角形判定定理和性质的运用．
26．如图，矩形PQMN内接于△ABC，矩形周长为24，AD⊥BC交PN于E，且BC＝10，AE＝16，求△ABC的面积．
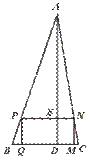
【提示】利用相似三角形的性质，列出关于ED的方程，求ED的长，即可求出S△ABC．
【答案】∵ 矩形PQMN，
∴ PN∥QM，PN＝QM．∵ AD⊥BC，
∴ AE⊥PN．∵ △APN∽△ABC，
∴ 
＝
．
设ED＝x，又 矩形周长为24，则
PN＝12－x，AD＝16＋x．
∴ 
＝
．即 x2＋4x－32＝0．解得 x＝4．
∴ AD＝AE＋ED＝20．∴ S△ABC＝BC·AD＝100．
【点评】本题要求运用相似三角形对应高线的比等于相似比．
（四）证明题：（每题6分，共24分）
27．已知：如图，在正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点．求证：△ADQ∽△QCP．
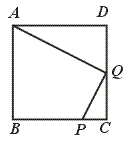
【提示】先证
＝
．
【答案】在正方形ABCD中，
∵ Q是CD的中点，∴ ＝2．
∵ 
＝3，∴ 
＝4．
又 BC＝2DQ，∴ 
＝2．
在△ADQ和△QCP中，＝，∠C＝∠D＝90°，
∴ △ADQ∽△QCP．
【点评】本题要求运用相似三角形的判定定理．
28．已知：如图，△ABC中，AB＝AC，AD是中线，P是AD上一点，过C作CF∥AB，延长BP交AC于E，交CF于F．求证：BP2＝PE·PF．
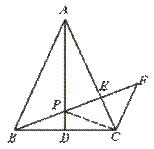
【提示】先证PB＝PC，再证△EPC∽△CPF．
【答案】连结PC．
∵ AB＝AC，AD是中线，∴ AD是△ABC的对称轴．
∴ PC＝PB，∠PCE＝∠ABP．∵ CF∥AB，
∴ ∠PFC＝∠ABP．∴ ∠PCE＝∠PFC．
又 ∠CPE＝∠EPC，∴ △EPG∽△CPF．
∴ 
＝
．即 PC2＝PE·PF．∴ BP2＝PE·PF．
【点评】本题要求运用等腰三角形的性质以及相似三角形的判定与性质．
29．如图，BD、CE为△ABC的高，求证∠AED＝∠ACB．
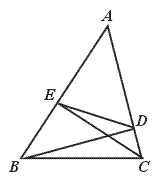
【提示】先证△ABD∽△ACE，再证△ADE∽△ABC．
【答案】∵ ∠ADB＝∠AEC＝90°，∠A＝∠A，
∴ △ABD∽△ACE．∴ 
＝．
又 ∠A＝∠A，∴ △ADE∽△ABC．∴ ∠AED＝∠ACB．
【点评】本题要求运用相似三角形的判定与性质．
30．已知：如图，在△ABC中，∠C＝90°，以BC为边向外作正方形BEDC，连结AE交BC于F，作FG∥BE交AB于G．
求证：FG＝FC．
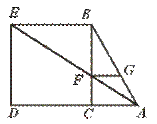
【提示】证明
＝
．
【答案】∵ FG∥BE，∴ ＝
．∵ FC∥ED，∴ ＝．
∴ ＝．又 EB＝ED，∴ FG＝FC．
（五）解答题（8分）
31．（1）阅读下列材料，补全证明过程：
已知：如图，矩形ABCD中，AC、BD相交于点O，OE⊥BC于E，连结DE交
OC于点F，作FG⊥BC于G．求证：点G是线段BC的一个三等分点．
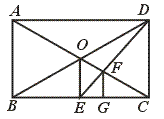
证明：在矩形ABCD中，OE⊥BC，DC⊥BC，
∴ OE∥DC．∵ 
＝，∴ 
＝＝．∴ 
＝．
……
（2）请你仿照（1）的画法，在原图上画出BC的一个四等分点（要求保留画图痕迹，可不写画法及证明过程）．
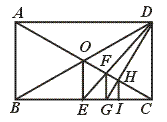
【提示】先证FG∥DC，再证
＝或
＝
．
【答案】（1）补全证明过程，方法一：
∵ FG⊥BC，DC⊥BC，
∴ FG∥DC．
∴ 
＝＝．
∵ AB＝DC，
∴ ＝．
又 FG∥AB，
∴ 
＝＝．
方法二：
∵ FG⊥BC，DC⊥BC，
∴ FG∥DC．
∴ 
＝＝．
∴ ＝．
∵ E是BC的中点，
∴ 
＝
＝
＝．
∴ 点G是BC的一个三等分点．
（2）如图，中点I．