《一元一次不等式》基础测试

《一元一次不等式》基础测试

（一）填空题（每空2分，共32分）

1．已知a＜b＜0，用不等号连结下列各题中的两式：

（1）a－5_____b－5；　　（2）－a_____－b；　　（3）b－a_____0；

（4）a_____b；　　　　（5）a³_____b³； 　　　　　（6）_____．

【提示】根据不等式的基本性质及式子的意义判断．

【答案】（1）＜；（2）＞；（3）＞；（4）＞；（5）＜；（6）＞．

2．x的与5的差不小于－4的相反数，用不等式表示为_____．

【提示】“不小于”就是“大于或等于”．【答案】x－5≥4．

3．若x＜a＜0，则把x ² ，a² ，ax从小到大排列是_______．【答案】a²＜ax＜x ²．

4．已知不等式mx－n＞0，当m____时，不等式的解集是x＜；当m____时，不等式的解集是x＞．【答案】m＜0；m＞0．

5．当x____时，代数式的值是负数；当x_____时，代数式的值是非负数．

【答案】x＜；x≤．

6．不等式4 x－3≤7的正整数解是_______．【答案】2，1．

7．不等式组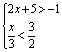的整数解的和是_______，积是_______．【答案】7，0．

8．不等式－1＜≤4的解集是_______．【答案】－＜x≤3．

（二）选择题（每小题3分，共24分）

9．下列各式中一定成立的是……………………………………………………………（　　）

（A）a＞－a 　（B）－4a＜－a　 （C）a－3＜a＋3　 （D）a²＞－a²

【提示】（D）中当a＝0时，不等式不成立．换言之，此不等式仅当a≠0时才成立．【答案】C．

10．由m＞n，得am≤an的条件是……………………………………………………（　　）

（A）a＞0　　 （B）a＜0　　 （C）a≥0　　（D）a≤0【答案】D．

11．若2 x－5＝5－2 x，则x的取值是…………………………………………………（　　）

（A）x＞　　（B）x≥　　（C）x＜　　（D）x≤

【提示】根据绝对值的意义，得5－2 x≥0．【答案】D．

12．若方程5 x－2a＝8的解是非负数，则a的取值是…………………………………（　　）

（A）a＞－4　　（B）a＜－4　　（C）a≥－4　　（D）a≤－4

【提示】根据题意，得≥0．【答案】C．

13．若a＜b，则不等式组………………………………………………………（　　）

（A）解集是x＜a　（B）解集是x＞b　（C）解集是b＜x＜a　（D）无解【答案】D．

14．使不等式x＋1＞4 x＋5成立的最大整数是………………………………………（　　）

（A）1　　（B）0　　（C）－1　　（D）－2【提示】根据题意，得≥0．

【答案】D．

15．不等式组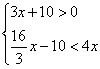的最小整数解是………………………………………（　　）

（A）－4　　（B）－3　　（C）－2　　（D）7

【提示】先解不等式组，再找出解集中的最小整数．【答案】B．

16．若不等式组有解，则k的取值范围是…………………………………（　　）

（A）k＜2　　 （B）k≥2　　 （C）k＜1　　 （D）1≤k＜2【答案】A．

（三）解下列不等式或不等式组（每小题4分，共20分）

17．5－≥3－．【答案】x≥－10．

18．－1＜＋．【答案】y＞．

19．【答案】－1＜x＜．

20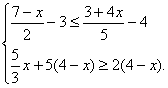．【答案】3≤x≤9．

21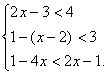．【答案】＜x＜3．

（四）解答题（每小题8分，共24分）

22．当2（k－3）＜时，求关于x的不等式＞x－k的解集．

【提示】先解关于k的不等式，求出k的取值，再根据k的取值，解关于x的不等式．

【答案】解2（k－3）＜，得k＜4，所以x＜．

23．求满足3－≤5－且小于－7的整数y．

【提示】即求不等式组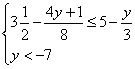的整数解．

【答案】－9≤y＜－7，所以　y＝－8，－9．

24．已知满足不等式3（x－2）＋5＜4（x－1）＋6的最小整数是方程2 x－ax＝3的解，求代数式4a－的值．

【提示】先求不等式解集中的最小整数，再代入方程求出a的值．

【答案】x＞－3，最小整数x＝－2，a＝，10．