中考数学全真模拟试题(二)
一、选择题(每题3分,共33分)
1、抛物线![]() 的对称轴是( )
的对称轴是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、二次函数![]() 的图象如图所示,则( )
的图象如图所示,则( )
A、![]() ,
,![]() B、
B、![]() ,
,![]()
C、![]() ,
,![]() D、
D、![]() ,
,![]()
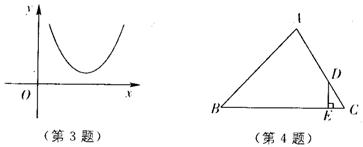
4、如图,在![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,垂足为点
,垂足为点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、给出下列命题:
①平行四边形的对角线互相平分;②对角线互相平分的四边形是平行四边形;③菱形的对角线互相垂直;④对角线互相垂直的四边形是菱形。其中真命题的个数为( )
A、4 B、3 C、2 D、1
6、给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中,
。其中,![]() 随
随![]() 的增大而减小的函数是( )
的增大而减小的函数是( )
A、①② B、①③ C、②④ D、②③④
7、已知一次函数![]() 与
与![]() ,它们在同一坐标系内的大致图象是( )
,它们在同一坐标系内的大致图象是( )
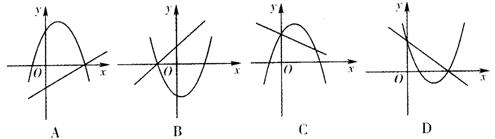
8、如图,![]() 是不等边三角形,
是不等边三角形,![]() ,以点
,以点![]() 、
、![]() 为两个顶点作位置不同的三角形,使所作三角形与
为两个顶点作位置不同的三角形,使所作三角形与![]() 全等,这样的三角形可以作出( )
全等,这样的三角形可以作出( )
A、2个 B、4个 C、6个 D、8个
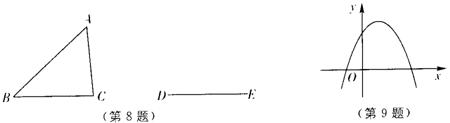
9、二次函数![]() 的图象如图所示,那么下列四个结论:①
的图象如图所示,那么下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,正确的结论有( )
中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个
10、如图,在梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则此梯形的面积是( )
,则此梯形的面积是( )
A、24 B、20 C、16 D、12
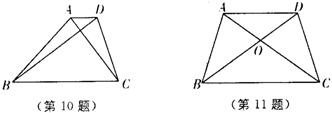
11、如图,线段![]() 、
、![]() 相交于点
相交于点![]() ,欲使四边形
,欲使四边形![]() 成为等腰梯形,应满足的条件是( )
成为等腰梯形,应满足的条件是( )
A、![]() ,
,![]() B、
B、![]() ,
,![]() ,
,![]()
C、![]() ,
,![]() D、
D、![]() ,
,![]()
 二、填空题(每题3分,共30分)
二、填空题(每题3分,共30分)
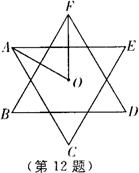
12、如图,点![]() 是正
是正![]() 和正
和正![]() 的中心,且
的中心,且![]() ∥
∥![]() ,则
,则![]() =_______。
=_______。
13、某次数学测验满分为100(单位:分),某班的平均成绩为75,方差为10。若把每位同学的成绩按满分120进行换算,则换算后的平均成绩与方差分别是_________。
14、李好在六月月连续几天同一时刻观察电表显示的度数,记录如下:
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | … | 30号 |
| 电表显示(度) | 120 | 123 | 127 | 132 | 138 | 141 | 145 | 148 | … |
估计李好家六月份总月电量是___________。
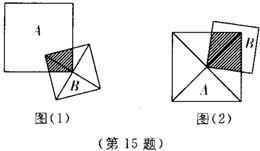
15、将正方形![]() 的一个顶点与正方形
的一个顶点与正方形![]() 的对角线交叉重合,如图⑴位置,则阴影部分面积是正方形
的对角线交叉重合,如图⑴位置,则阴影部分面积是正方形![]() 面积的
面积的![]() ,将正方形
,将正方形![]() 与
与![]() 按图⑵放置,则阴影部分面积是正方形
按图⑵放置,则阴影部分面积是正方形![]() 面积的____________。
面积的____________。
16、抛物线![]() 的顶点关于
的顶点关于![]() 轴对称的点的坐标为_________。
轴对称的点的坐标为_________。
17、在![]() 中,
中,![]() ,
,![]() 是斜边
是斜边![]() 上的中线,将
上的中线,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,如果
处,如果![]() 恰好与
恰好与![]() 垂直,那么
垂直,那么![]() 等于________度。
等于________度。
18、已知![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,连结
的中点,连结![]() 、
、![]() ,在不再连结其他线段的前提下,要使四边形
,在不再连结其他线段的前提下,要使四边形![]() 成为菱形,还需添加一个条件,这个条件可以是__________。
成为菱形,还需添加一个条件,这个条件可以是__________。
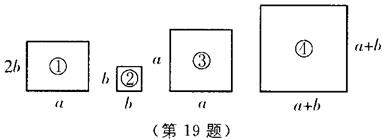
19、下列四个图形中,图①是长方形,图②、③、④是正方形。把图①、②、③三个图形拼在一起(不重合),其面积是![]() ,则
,则![]() _________,图④的面积
_________,图④的面积![]() _________,则
_________,则![]() ________
________![]() (填“>”“=”或“<”)。
(填“>”“=”或“<”)。
20、已知方程![]() (
(![]() ,
,![]() ,
,![]() 是常数),请你通过变形把它写成你所熟悉的一个函数表达式的形式,则函数表达式为______________,成立的条件是________,是_____________函数。
是常数),请你通过变形把它写成你所熟悉的一个函数表达式的形式,则函数表达式为______________,成立的条件是________,是_____________函数。
21、如图,在平行四边形![]() 中,点
中,点![]() 、
、![]() 在对角线
在对角线![]() 上,且
上,且![]() 。请你以点
。请你以点![]() 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)。
为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)。
⑴连结:___________;
⑵猜想:___________=__________;
⑶证明:______________。
三、解答题(22~26题每题6分,27题7分,共37分)
22、如图,矩形![]() 中,点
中,点![]() 是
是![]() 与
与![]() 的交点,过点
的交点,过点![]() 的直线与
的直线与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() 。
。
⑴求证:![]() ;
;
⑵当![]() 与
与![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形?并证明你的结论。
是菱形?并证明你的结论。
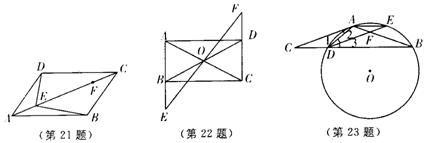
23、如图,![]() 是
是![]() 的弦,
的弦,![]() 切
切![]() 于点
于点![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连结
的中点,连结![]() ,在不添加辅助线的情况下,
,在不添加辅助线的情况下,
⑴找出图中存在的全等三角形,并给出证明;
⑵图中存在你所学过的特殊四边形吗?如果存在,请你找出来并给出证明。
24、操作:将一把三角尺放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() 。
。
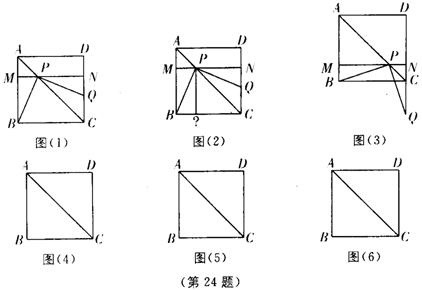
探究:设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() 。
。
⑴当点![]() 在
在![]() 上时,线段
上时,线段![]() 与线段
与线段![]() 之间有怎样的大小关系?试证明你观察得到的结论(如图⑴)。
之间有怎样的大小关系?试证明你观察得到的结论(如图⑴)。
⑵当点![]() 在边
在边![]() 上时,设四边形
上时,设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域(如图⑵)。
之间的函数解析式,并写出函数的定义域(如图⑵)。
⑶当点![]() 在线段
在线段![]() 上滑动时,
上滑动时,![]() 是否可能成为等腰三角形?如果可能,指出所有能使
是否可能成为等腰三角形?如果可能,指出所有能使![]() 成为等腰三角形的点
成为等腰三角形的点![]() 的位置,并求出相应的
的位置,并求出相应的![]() 的值;如果不可能,试说明理由(如图⑶)。(图⑷、图⑸、图⑹的的形状、大小相同,图⑷供操作、实验用,图⑸和图⑹备用)
的值;如果不可能,试说明理由(如图⑶)。(图⑷、图⑸、图⑹的的形状、大小相同,图⑷供操作、实验用,图⑸和图⑹备用)
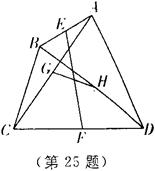 25、如图,已知四边形
25、如图,已知四边形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,并且点
的中点,并且点![]() 、
、![]() 、
、![]() 、
、![]() 有在同一条直线上。
有在同一条直线上。
求证:![]() 和
和![]() 互相平分。
互相平分。
26、已知:抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() 。
。
⑴求抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标。
的坐标。
⑵点![]() 是抛物线与
是抛物线与![]() 轴的交点,点
轴的交点,点![]() 是抛物线上的一点,且以
是抛物线上的一点,且以![]() 为一底的梯形
为一底的梯形![]() 的面积为9,求此抛物线的解析式。
的面积为9,求此抛物线的解析式。
⑶点![]() 是第二象限内到
是第二象限内到![]() 轴、
轴、![]() 轴的距离的比为5:2的点,如果点
轴的距离的比为5:2的点,如果点![]() 在⑵中的抛物线上,且它与点
在⑵中的抛物线上,且它与点![]() 在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点
在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
27、在平面直角坐标系中(单位长度:1cm),![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始以2cm/s的速度沿折线
开始以2cm/s的速度沿折线![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 开始以1cm/s的速度沿折线
开始以1cm/s的速度沿折线![]() 运动。
运动。
⑴在运动开始后的每一时刻一定存在以点![]() 、
、![]() 、
、![]() 为顶点的三角形和以点
为顶点的三角形和以点![]() 、
、![]() 、
、![]() 为顶点的三角形吗?如果存在,那么以点
为顶点的三角形吗?如果存在,那么以点![]() 、
、![]() 、
、![]() 为顶点的三角形和以点
为顶点的三角形和以点![]() 、
、![]() 、
、![]() 为顶点的三角形相似吗?以点
为顶点的三角形相似吗?以点![]() 、
、![]() 、
、![]() 为顶点的三角形和以点
为顶点的三角形和以点![]() 、
、![]() 、
、![]() 为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
⑵试判断![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆与以点
为半径的圆与以点![]() 为圆心、
为圆心、![]() 半径的圆的位置关系;除此之外
半径的圆的位置关系;除此之外![]() 与
与![]() 还有其他位置关系吗?如果有,请求出
还有其他位置关系吗?如果有,请求出![]() 的取值范围。
的取值范围。
⑶请你选定某一时刻,求出经过三点![]() 、
、![]() 、
、![]() 的抛物线的解析式。
的抛物线的解析式。
2007年中考数学全真模拟试题(二)
参考答案与提示
1、A 2、D 3、A 4、D 5、B 6、D 7、C 8、B 9、D 10、A 11、D 12、60° 13、90 14、4 120度 15、![]()
16、![]() 17、30 18、
17、30 18、![]() ,
,![]() ,
,![]() 等 19、
等 19、![]()
![]() = 20、
= 20、![]()
![]() 二次 21、⑴
二次 21、⑴![]() ⑵
⑵![]()
![]() ⑶
⑶![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ∥
∥![]() 。
。![]() ,在
,在![]() 和
和![]() 中,
中,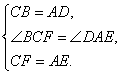
![]() ,
,![]() 。
。
22、⑴![]() 在矩形
在矩形![]() 中有
中有![]() ∥
∥![]() ,
,![]() ,
,![]() 。又
。又![]() ,
,![]() 。
。
⑵当![]() 与
与![]() 垂直时,四边形
垂直时,四边形![]() 是菱形。
是菱形。![]() ,
,![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是平行四边形。又
是平行四边形。又![]() ,
,![]() 四边形
四边形![]() 是菱形。
是菱形。
23、⑴![]() 。证明:
。证明:![]() ,
,![]() 。
。![]() 为
为![]() 的切线,
的切线,![]() 。
。![]() 。又
。又![]() ,
,![]() 。又
。又![]() ,即
,即![]() 。
。![]() 。在
。在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
⑵存在,它们分别为平行四边形![]() 和梯形
和梯形![]() 。证明:
。证明:![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() 。
。![]() 四边形
四边形![]() 是平行四边形。又
是平行四边形。又![]() 与
与![]() 相交,
相交,![]() 四边形
四边形![]() 为梯形。
为梯形。
24、⑴![]() ,证明:过点
,证明:过点![]() 作
作![]() ∥
∥![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则四边形
,则四边形![]() 和四边形
和四边形![]() 都是矩形,
都是矩形,![]() 和
和![]() 都是等腰三角形(如图⑴)。
都是等腰三角形(如图⑴)。![]() ,
,![]() ,
,![]() 。而
。而![]() ,
,![]() 。又
。又![]() ,
,![]() ,
,![]() 。
。
⑵由⑴知![]() ,得
,得![]() 。
。![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() ,
,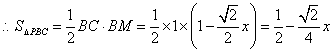 ,
,![]()
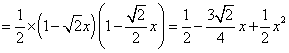 ,
,![]()
![]() ,即
,即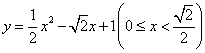 。
。
⑶![]() 可能成为等腰三角形。①当点
可能成为等腰三角形。①当点![]() 与点
与点![]() 重合,点
重合,点![]() 与点
与点![]() 重合,这时
重合,这时![]() ,
,![]() 是等腰三角形,此时
是等腰三角形,此时![]() ;②当点
;②当点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() 时,
时,![]() 是等腰三角形(如图3),此时,
是等腰三角形(如图3),此时,![]() ,
,![]() ,
,![]() ,
,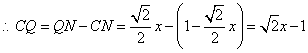 ,当
,当![]() 时,得
时,得![]() 。
。
25、连结![]() 、
、![]() 、
、![]() 、
、![]() 。点
。点![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点。在
的中点。在![]() 中,
中,![]() ;在
;在![]() 中,
中,![]() ,
,![]() 。
。![]() 四边形
四边形![]() 为平行四边形。
为平行四边形。![]() 与
与![]() 互相平分。
互相平分。
26、⑴依题意,抛物线的对称轴为![]() 。
。![]() 抛物线与
抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ,
,![]() 由抛物线的对称性,可得抛物线与
由抛物线的对称性,可得抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标为
的坐标为![]() 。
。
⑵![]() 抛物线
抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,
,![]() 。
。![]() ,
,![]() ,
,![]() ,
,![]() 点
点![]() 的坐标为
的坐标为![]() 。又梯形
。又梯形![]() 中,
中,![]() ∥
∥![]() ,且点
,且点![]() 在抛物线
在抛物线![]() 上,
上,![]() 点
点![]() 的坐标为
的坐标为![]() 。
。![]() 梯形
梯形![]() 的面积为9,又
的面积为9,又![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所求抛物线的解析式为
所求抛物线的解析式为![]() 或
或![]() 。
。
⑶设点![]() 的坐标为
的坐标为![]() ,依题意,
,依题意,![]() ,
,![]() ,且
,且![]() ,
,![]() 。
。
①设点![]() 在抛物线
在抛物线![]() 上,则
上,则![]() 。解方程组
。解方程组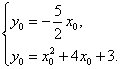 得
得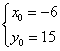 ,
,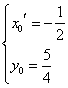 ,
,![]() 点
点![]() 与点
与点![]() 在对称轴
在对称轴![]() 的同侧,
的同侧,![]() 点
点![]() 的坐标为
的坐标为![]() 。设在抛物线的对称轴
。设在抛物线的对称轴![]() 上存在一点
上存在一点![]() ,使
,使![]() 的周长最小。
的周长最小。![]() 长为定值,
长为定值,![]() 要使
要使![]() 的周长最小,只需
的周长最小,只需![]() 最小。
最小。![]() 点
点![]() 关于对称轴
关于对称轴![]() 的对称点是
的对称点是![]() ,
,![]() 由几何知识可知,点
由几何知识可知,点![]() 是直线
是直线![]() 与对称轴
与对称轴![]() 的交点。设过点
的交点。设过点![]() 、
、![]() 的直线的解析式为
的直线的解析式为![]() ,则
,则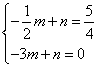 ,解得
,解得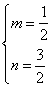 ,
,![]() 直线
直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入上式,得
代入上式,得![]() ,
,![]() 点
点![]() 的坐标为
的坐标为![]() 。
。
②设点![]() 在抛物线
在抛物线![]() 上,则
上,则![]() 。解方程组
。解方程组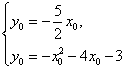 消去
消去![]() ,得
,得![]() ,
,![]() ,
,![]() 此方程无实数根。综上所述,在抛物线的对称轴上存在点
此方程无实数根。综上所述,在抛物线的对称轴上存在点![]() ,使
,使![]() 的周长最小。
的周长最小。
27、⑴①不一定。例如:当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 与点
与点![]() 、
、![]() 、
、![]() 都不能构成三角形。②当
都不能构成三角形。②当![]() 时,即当点
时,即当点![]() 、
、![]() 在
在![]() 轴的正半轴上时,
轴的正半轴上时,![]() 。这是因为:
。这是因为:![]() ,
,![]() ,
,![]() 。③会成为等腰直角三角形。这是因为:当
。③会成为等腰直角三角形。这是因为:当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() 为等腰直角三角形。同理可得,当
为等腰直角三角形。同理可得,当![]() 时,
时,![]() 为等腰直角三角形。
为等腰直角三角形。
⑵①当![]() 时,
时,![]() ,
,![]() ,同理可得
,同理可得![]() ,
,![]() ,
,![]() 此时
此时![]() 与
与![]() 内切。②有。当外高时,
内切。②有。当外高时,![]() ;当外切时,
;当外切时,![]() ;当相交时,
;当相交时,![]() ;当内含时,
;当内含时,![]() 。
。
⑶当![]() 时,
时,![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,设经过点
,设经过点![]() 、
、![]() 、
、![]() 的抛物线的解析式为
的抛物线的解析式为![]() ,则
,则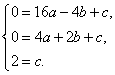 解得
解得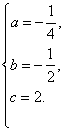 故所求解析式为
故所求解析式为![]() 。
。