中考数学月考试题
A卷(共100分)
一、选择题：(每小题3分，共24分)
1．2的算术平方根是（ ）
(A)
(B)－ (C)± (D)2
2．右边几何体的主视图是（ ）
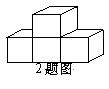
(A) (B) (C) (D)
3．为了估计湖中有多少条鱼，先从湖中捕捉50条鱼做记号，然后放回湖里，经过一段时间，等带记号的鱼完全混于鱼群中之后，再捕捞第二次鱼共200条，有10条做了记号，则估计湖里有（ ）条鱼。
A．400 B． 500 C． 800 D． 1000
4．去年成都市接待入境旅游者约876000人，这个数可以用科学记数法表示为（ ）
(A)
(B)
(C)
(D)
5．在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )
(A) (B) (C) (D)
6．某出租车司机从双流客运中心送一游客到双流机场，停留一段时间后，又驱车原路返回客运中心，假设出租车保持匀速行驶，下面图象中，能较好刻画整个过程中该出租车到客运中心的距离S(千米)与行驶时间
(时)的关系图是（ ）
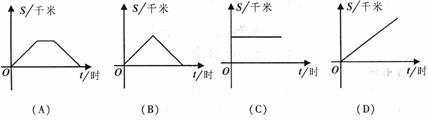
7．我国古代数学巨著《孙子算经》中的“难兔同笼”题为：“今有雉(鸡)兔同笼，上有三十五头，下有九十四足．问雉兔各几何?”．正确答案是（ ）
(A)鸡24只，兔11只 (B)鸡23只，兔12只
(C)鸡11只，兔24只 (D)鸡12只，兔23只
 | |||
 | |||
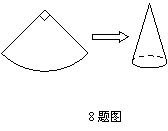
8．如图，现有一圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（ ）
(A)4cm (B)3cm (C)2cm (D)1cm
二、填空题：(每小题3分，共24分)
9．在函数
中，自变范围量x的取值是__________；
10．分解因式： 4a3－4a2＋a＝__________；
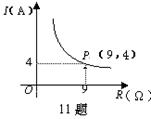
11．某种蓄电池的电压为定值，使用此电源时，电流 I（A）与可变电阻 R（Ω）之间的函数关系如图所示，当用电器的电流为10A时，用电器的可变电阻为_______Ω；
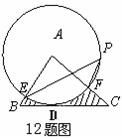12．如图，在△ABC
中，BC
＝4，以点A为圆心、2为半径的⊙A与BC相切于点D，交AB于E，交 AC于F， 点P是⊙A上的一点，且∠EPF＝40°， 则图中阴影部分的面积是
；
13．某商场举办有奖销售活动，购物每满100元者发兑奖券一张，在10000张兑奖券中，设特等奖1个，一等奖10个，二等奖100个．若某人购物100元，那么他中奖的概率是___________；
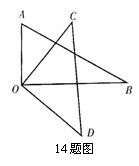
14．如图，将一副三角板叠放在一起，使直角顶点重合于点O，如果
，那么
__________度；
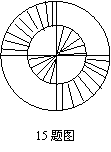
15．如图，是两个同心圆，其中两条直径互相垂直，大圆的半径是2，则图中阴影部分面积和为____________；
 |
16．已知
是方程
的两根，则
的值是________.
三、(共18分)
17．解答下列各题(每小题6分)
(1)计算：
(2)请你先化简
，再选取一个你喜欢又使原式有意义的数代入求值．
(3)解不等式组
，并把解集在数轴上表示出来．
四、(每小题8分，共16分)
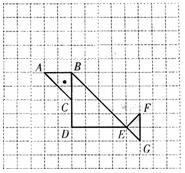18．如右图，正方形网格中有一幅美丽的图案：“天高任鸟飞”．
(1)若每个小正方形的边长为1，求这只小鸟
所占的面积；
(2)在右图中，以C为中心，将小鸟逆时针方
向旋转
，画出旋转后的图形．
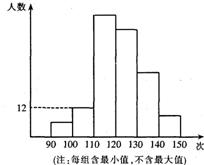19.某校为了了解九年级学生的体能情况，抽调了一部分学生进行一分钟跳绳测试，将测试成绩整理后作出如下统计图．甲同学计算出前两组的频率和是0.12，乙同学计算出跳绳次数不少于100次的同学占96％，丙同学计算出从左至右第二、三、四组的频数比为4：17：15．结合统计图回答下列问题：
(1)这次共抽调了多少人?
(2)若跳绳次数不少于130次为优秀，则这次测试成绩的优秀率是多少?
(3)如果这次测试成绩的中位数是120次，那么这次测试中，成绩为120次的学生至少有多少人?
五、(每小题9分，共18分)
20．如图，在梯形ABCD中，AD∥BC, 
，
．（1）探索BD、CD的位置关系，并说明理由;（2）若
，求梯形ABCD的面积．
21．双流县是全国三大草莓生产基地之一，也是全国最大的冬草莓生产基地，今年又喜获丰收．四川在线(2006—01—12 09：49：53)报道：
双流草莓俏销北方城市
目前，正值北方寒冷的冬季，而双流清晨摘下的还带着晨露的草莓，当天就可以出现在省外各大超市的货架上．据统计，每天从双流机场运往全国各地的草莓达数十吨，主要运往乌鲁木齐、北京、长春、沈阳、郑州等北方城市．双流的草莓到达外地后，身价翻番．
问题：草莓1～5月份的批发价可近似地看作是时间(月份)的一次函数，今年1月份批发价为6元／kg，4月份批发价为2.4元／kg。
(1)求草莓批发价
(元)与时间(月份)的函数关系式；
(2)在3月份，有一商家以批发价收购了一批草莓(不足5000kg)，有两种销售方案：
方案一：在本地销售，每千克价格为5元；
方案二：运往沈阳销售，每千克价格为10元，但需花费5000元的运输费．
假设商家收购的草莓都能及时全部售出，根据上述两种销售方案，请你分别写出商家所获利润
(元)和销售草莓质量
(kg)之间的函数关系式；
(3)在(2)的条件下，当销售量在什么范围时，选择哪种销售方案对商家更有利?请说明理由．
B卷(共50分)
一、填空题：(每小题3分，共15分)
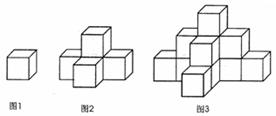22．图1是—个一面靠墙水平摆放的小正方体木块，图2、图3是由这样的小正方体木块靠墙叠放而成，按照这样的规律叠放下去，第5个叠放的图形中，小方体木块的个数是_____________个．
23．对实数
，定义运算“
”使
，则不等式
的解集是______________.
24．设双曲线
与直线
的交点为A，B两点，则S⊿AOB = .
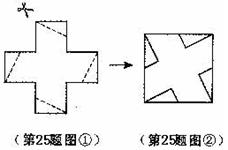
25．将一个无盖正方形纸盒展开（如图①），沿虚线剪开，用得到的5张纸片（其中4张是全等的直角三角形纸片）拼成一个正方形（如图②），则所剪得的直角三角形较短的与较长的直角边的比是 .
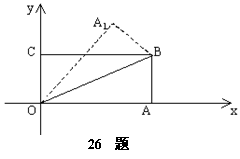
26． 如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在
处，已知
，
，则点的坐标是 .
二、解答题(28、29每小题7分，30题10分，31题11分，共35分)
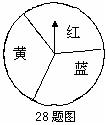
28．小明和小亮用如下的同一个转盘进行“配紫色”游戏。游戏规则如下：连续转动两次转盘，如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则可配成紫色），则小明得1分，否则小亮得1分。你认为这个游戏对双方公平吗？请说明理由；若不公平，请你修改规则使游戏对双方公平。
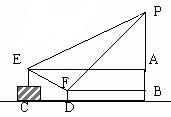29．广场上有一个充满氢气的气球P，被广告条拽着悬在空中，甲乙二人分别站在E，F处，他们看气球的仰角分别为
、
，E点与F点的高度差AB为1米，水平距离CD为5米，FD的高度为0.5米，请问此气球有多高？
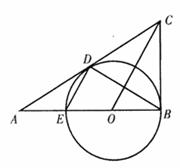
30．如图，在△ABC中，
，O是AB上一点，以O为圆心，OB为半径的圆与AB相交于点E，与AC相切于点D，连接DB、DE、O(C)
(1)从图中找出两对相似三角形(不添加任何字母和辅助线)；
(2)在(1)中已找出的两对相似三角形中，选择其中一对，写出其证明过程；
(3)若圆O的直径为3cm，且
，求CD的长．
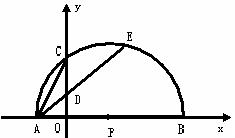
31．如图，已知两点A(-1,0)、B（4，0）在x轴上，以AB为直径的半圆P交y轴于点C.（1）求经过A、B、C三点的抛物线的解析式。
（2）设AC的垂直平分线交OC于D，连接AD并延长AD交半圆P于点E
，弧AC与弧CE相等吗？请证明你的结论；
（3）设点M为X轴负半轴上的一点，OM=
AE，是否存在过点M的直线，使该直线与（1）中所得的抛物线的两个交点到y轴的距离相等？若存在，求出这条直线对应的解析式，若不存在，请说明理由。