初中毕业生数学学业模拟试卷

一、选择题、（本题有10小题，每小题4分，共40分）

1、4的平方根是（　　）

A、2　　  B、±2　　　C 、4　　  D、±4　　　　　　　　　　　　　　 

2、如图：在平面直角坐标系中，点E的坐标是（　　）

A、（1，3）　　B、（3，1）　 C、（-1，3）　 D、（1，-3）

3、如图Rt△ABC∽Rt△DEF，∠C=∠F=90°，点A与点D　　　　　　 （第2题）

为对应点，∠B=60°，则∠E的度数（　　）　　　　　　　　　　 （第2题）

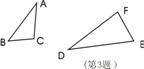A、30°　　B、45°　　C、60°　　D、90°

4、二次函数y=2（x–1）²-1的顶点坐标是（　　　　  ）

A （-1，-1）　 B （1，-1）　 C （-1，1）　 D （1，1）

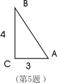5、已知如图Rt△ABC中，∠C=90°，AC=3，BC=4，那么下列各式中，正确的是（　　）

A、tanB=　 B、tanA=　

 C、cosB=　 D、cosA=

6、如图将一块正方形纸片沿对角线折叠一次，然后在得到的三角菜的三个角上各挖去一个圆洞，最后将正方形纸片展开，得到的图案是（　　 ）

A、　　　　B、　　  C、　　　 D、

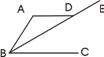7、如图AD∥BC，若∠ADB=25°，则∠DBC的度数为（　　 ）

A、155°　 B、50°　　C、45°　　D、25°

8、有一个1万人的小镇，随机调查3000人，其中450人　　　　　　 （第7题）

看中央电视台的晚间新闻，在该镇随便问一人，他（她）看中央电视晚间新闻的概率是（　　　）

A、　　B、　　 C、0　　D、1

9、刘翔为了备战2008年奥运会，刻苦进行110米跨栏训练，为判断他的成绩是否稳定，教练对他10次训练进行统计分析，则教练需了解刘翔这10次成绩的（  　 ）

A、众数　　 B、方差　　 C、平均数　　 D、频数

10、若用（1）（2）（3）（4）四幅图象分别表示变量之间的关系，将下面的（a）（b）（c）（d）对应的图象排序；

（a）面积为定质的矩形；（矩形的相邻两边长的关系）。

（b）运动员推出去的铅球；（铅球的高度与时间的关系）。

（c）一个弹簧不挂重物到逐渐挂重物；（弹簧长度与所挂重物质量的关系）。

（d）某人从A地到B地后，停留一段时间，然后按原速返回；（离开A地的距离与时间的关系）。

其中正确的顺序是（　　）

A、（3）（4）（1）（2）　　  B、（3）（2）（1）（4）

C、（4）（3）（1）（2）　　  D、（3）（4）（2）（4）

二、填空题（本题有6小题，每小题5分，共30分）

11、方程的解为____________。

12、温家宝总理在十届全国人大四次会议上谈到解决关于“三农”问题时说，2006年中央财政用于“三农”的支出将达到万元，这个数据用科学工作者记数法可表示为_________万元。

13、反比例函数的图象经过点（-2，1），则=______。

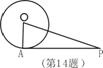
14、如图PA是⊙O的切线，切点为A，PA=，

∠APO=30°，则 ⊙O的半径长为________。

15、如图，扇形AOB的圆心角为直角，边长为1的

正方形OCDE的顶点，C、E、D分别在OA、OB、弧AB上，

过点A作AF⊥ED，交ED的延长线于点F，则图中阴影

部分的面积S=_________。

16、如图，A是硬币圆周上一点，硬币与数轴相切于原点O（A与O点重合），假设硬币的直径为1个单位长度。若将硬币沿数轴正方向滚动10周，点A恰好与数轴上点A´重合，则点A´对应的实数是_______。

三、解答题（本题有8小题）

17、（本题10分）

（1）计算：　　　 （2）计算：

18、（本题8分）已知点M、N分别是平行四边形ABCD的边AB、DC的中点，求证：∠DAN=∠BCM

19、某地共有100家供应快餐的饭店，环保部门为了了解一天共用了多少个一次性快餐饭盒，对其中10家饭店一天使用一次性快餐饭盒的个数作了调查，获得以下数据：

一天使用饭盒的个数（单位：个）	100	110	120	130	140	150
饭店数量（单位：家）	2	2	3	1	1	1

（1）求这10家饭店平均每家一天使用一次性快餐饭盒多少个？

（2）估计这100家饭店一天共使用一次性快餐饭盒的个数?

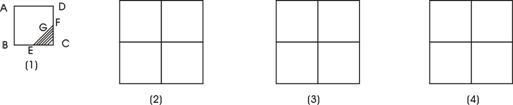
20、（本题10分）如图（1）所示的正方形ABCD，E、F分别是BC、CD的中点。用四块（1）中的正方形瓷砖拼成一个新的正方形，使拼成的图案是一个轴对称图形，请你在图（2）（3）（4）中各画一种拼法。（要求三种拼法各不相同，且其中至少有一个图形既是轴对称图形，又是中心对称图形）。

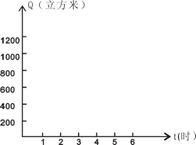
21、游泳池应定期换水，某游泳池在一次换水前存水1000立方米，换水时打开排水孔，以每时200立方米的速度将水放出，设放水时间为时，游泳池内的存水量为Q立方米。

（1）求Q关于的函数解析式和自变量的取值范围。

（2）请在右下图中作出函数图象，并根据图象写出放完游泳池内全部水需要多少时间？

O

22、国家为九年义务教育期间的学生实行“两免一补”政策，下表是我市某中学国家免费提供教科书补助的部分情况。

年级 项目	七	八	九	合计
每人免费补助金额（元）	110	90	50	——
免费补助的人数（人）	x	y	80	300
免费补助总金额（元）			4000	26200

（1）请将表格填写完整。

（2）列出方程组，求出七年级和八年级免费补助的人数。

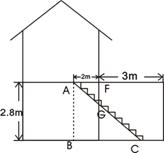
23、小王要装修自己带阁楼的新居（下图为新居剖面图），在建造客厅到阁楼的楼梯AC时，为避免上楼时墙角下碰头，设计墙角F到楼梯的竖直距离FG为1.75m，他量得客厅高AB=2.8m，楼梯洞口宽AF=2m，阁楼阳台宽EF=3m，请你帮助小王解决下列问题：

（1）要使墙角F到楼梯的竖直距离FG为1.75m，楼梯底端C至墙角D的距离CD是多少米？

（2）在（1）的条件下，为保证上楼时的舒适感，楼梯的每个台阶高要小于20cm，每个台阶宽要大于20cm，问小王应该将楼梯建几个台阶？为什么？

D

E

24、如图，已知抛物线，直线经过点B（0，2）。

（1）求的值；

（2）将直线绕着点B旋转到与轴平行的位置时（如图（1）），直线与抛物线相交，其中一个交点为P，求出点P的坐标；

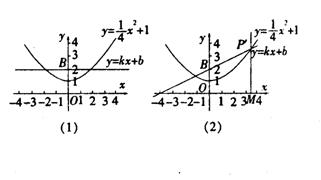（3）将直线继续绕着点B旋转，与抛物线相交，其中一个交点为P´（如图（2）），过点P´作轴的垂线P´M，点M为垂足，是否存在这样的点P´，使△P´BM为等边三角形？若存在，请求出点P´的坐标；若不存在，请说明理由。