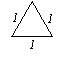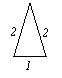初中三年级毕业考试数学试题
一.选择题(本大题共12个小题,每小题3分,共36分)。
01.函数![]() 中,自变量x的取值范围是( )。
中,自变量x的取值范围是( )。
A、x≥-1 B、x>2 C、x>-1且x≠2 D、x≥-1且x≠2

|
 | |||
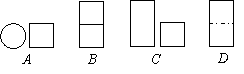 | |||
03.如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为( )。
A、120° B、100° C、140° D、90°
04.小华把自己一周的支出情况用如图所示的统计图表示出来,下列说法中,正确的是( )。
 A、从图中可以直接看出具体的消费数额
A、从图中可以直接看出具体的消费数额
B、从图中可以直接看出总消费数额
C、从图中可以直接看出各项消费数额占总消费数额的百分比
D、从图中可以直接看出各项消费数额在一周中的具体变化情况
05.化简![]() =( )。
=( )。
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
06.使用同一种规格的下列地砖,不能密铺的是( )。
A、正六边形地砖 B、正五边形地砖 C、正方形地砖 D、正三角形地砖
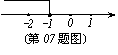
07.关于x的不等式2x-a≤-1的解集如图所示,则a的取值是( )。
A、0 B、-3 C、-2 D、-1
08.如图,一块实验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体( )。
 A、转过90° B、转过180° C、转过270° D、转过360°
A、转过90° B、转过180° C、转过270° D、转过360°
 | |||||
 | |||||
 | |||||
09.抛物线![]() 与x轴的两个不同交点是O和A,顶点B在直线
与x轴的两个不同交点是O和A,顶点B在直线![]() 上,则关于△OAB的判断正确的是( )。
上,则关于△OAB的判断正确的是( )。
A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形
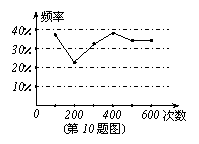
10.甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )。
A、掷一枚正六面体的骰子,出现1点的概率
B、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
C、抛一枚硬币,出现正面的概率
D、任意写一个整数,它能被2整除的概率
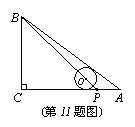
11.如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是( )。
A、1 B、![]() C、
C、![]() D、
D、![]()
12.中百超市推出如下优惠方案:(1)一次性购物不超过100元,不享受优惠;(2)一次性购物超过100元,但不超过300元一律9折;(3)一次性购物超过300元一律8折。某人两次购物分别付款80元、252元,如果他将这两次所购商品一次性购买,则应付款( )。
A、288元 B、332元 C、288元或316元 D、332元或363元
二.填空题(本大题共4个小题,每小题3分,共12分)。
13.据中新社报道:2010年我国粮食产量将达到540 000 000 000 kg,用科学记数法表示这个粮食产量为
kg。
14.已知关于x的不等式组![]() 的整数解共有6个,则a的取值范围是
。
的整数解共有6个,则a的取值范围是
。
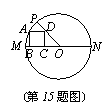
 15.如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为
。
15.如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45°,则AB的长为
。
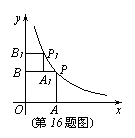
16.如图,已知反比例函数![]() 的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是
。
的图像上有一点P,过点P分别作x轴和y轴的垂线,垂足分别为A、B,使四边形OAPB为正方形。又在反比例函数的图像上有一点P1,过点P1分别作BP和y轴的垂线,垂足分别为A1、B1,使四边形BA1P1B1为正方形,则点P1的坐标是
。
三.解答题(本大题共9个小题,共计72分)。
17.(6分)先化简,再求值:![]() ·
·![]() ,其中
,其中![]() 。
。
18.(7分)已知关于x的一元二次方程x2+4x+m-1=0。
(1)请你为m选取一个合适的整数,使得到的方程有两个不相等的实数根;
(2)设α、β是(1)中你所得到的方程的两个实数根,求α2+β2+αβ的值。
 19.(7分)如图,小强在江南岸选定建筑物A,并在江北岸的B处观察,此时,视线与江岸BE所成的夹角是30°,小强沿江岸BE向东走了500m,到C处,再观察A,此时视线AC与江岸所成的夹角∠ACE=60°。根据小强提供的信息,你能测出江宽吗?若能,写出求解过程(结果可保留根号);若不能,请说明理由。
19.(7分)如图,小强在江南岸选定建筑物A,并在江北岸的B处观察,此时,视线与江岸BE所成的夹角是30°,小强沿江岸BE向东走了500m,到C处,再观察A,此时视线AC与江岸所成的夹角∠ACE=60°。根据小强提供的信息,你能测出江宽吗?若能,写出求解过程(结果可保留根号);若不能,请说明理由。
20.(7分)依据闯关游戏规则,请你探究“闯关游戏”的奥秘。闯关游戏规则:如图所示的面板上,有左右两组开关按钮,每组中的两个按钮均分别控制一个灯泡和一个发音装置。同时按下两组中各一个按钮,当两个灯泡都亮时闯关成功;当按错一个按钮时,发音装置就会发出“闯关失败”的声音。
(1)用列表的方法表示所有可能的闯关情况(只需列表即可);
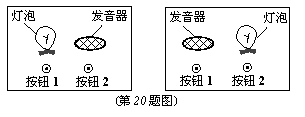 (2)求出闯关成功的概率。
(2)求出闯关成功的概率。
21.(7分)如图,已知P(m,a)是抛物线y=ax2上的点,且点P在第一象限。
(1)求m的值;
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M;
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
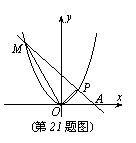 ②当b=4时,记△MOA的面积为S,求
②当b=4时,记△MOA的面积为S,求![]() 的最大值。
的最大值。
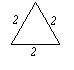
22.(8分)在平面内,分别用3根、5根、6根……火柴首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表表示如下,请阅读下表后再回答问题。
| 火柴数 | 3 | 5 | 6 |
| 示意图 |
|
|
|
| 形状 | 等边三角形 | 等腰三角形 | 等边三角形 |
问:(1)4根火柴能搭成三角形吗? 答: ;
(2)8根、12根火柴能搭成几种不同形状的三角形?并在下表中画出它们的示意图。
| 火柴数 | 8 | 12 |
| 示意图 | ||
| 形状 |
![]()
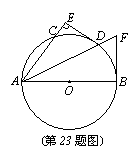 23.(9分)如图,AB为⊙O的直径,D是BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F。
23.(9分)如图,AB为⊙O的直径,D是BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F。
(1)求证:DE是⊙O的切线;
(2)若DE=3,⊙O的半径为5,求BF的长。
24.(10分)某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示。注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图像是线段,图乙的图像是抛物线。
请你根据图像提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?说明理由;
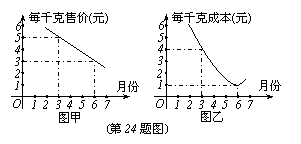 (3)已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?
(3)已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?
25.(11分)如图所示,在平面直角坐标系内,点A和点C的坐标分别为(4,8)、(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作EF∥CD交AC于点F。
(1)求经过A、C两点的直线的解析式;
(2)当点D在OB上移动时,能否使四边形CDEF成为矩形?若能,求出此时k、-b的指;若不能,请说明理由;
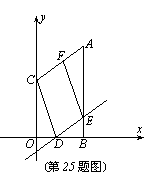 (3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。
(3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。