中考数学毕业会考模拟试卷(二)
一、选择题:本大题10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、冬季的一天室内温度是8℃,室外温度是-2℃,则室内外温度的差是( )
A.4℃ B.6℃ C.10℃ D.16℃
2、小马虎在下面的计算中只做对了一道题,他做对的题目是( )
A.(a-b)2=a2-b2 B.(-2a3)2=4a6 C.a3+a2=2a5 D.-(a-1)=-a-1
3、一种病毒非常微小,其半径约为0.m,用科学记数法可以表示为( )
A.1.6×106m B.1.6×10-6m C.1.6×10-7m D.1.6×10-8m
4、下列图形中是中心对称图形为( )

A B C D
5、把不等式组![]() 的解集表示在数轴上,正确的是(
)
的解集表示在数轴上,正确的是(
)

A B C D
 6、数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图4),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为( )
6、数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图4),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为( )
A.8,8 B.8,9 C.9,9 D.9,8
7、点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )
A.(![]() ) B.(-
) B.(-![]() ) C.(-
) C.(-![]() ,
,![]() ) D.(-
) D.(-![]() ,-
,-![]() )
)
8、⊙O1与⊙O2的半径分别为2和5,当O1O2=3.5时,两圆的位置关系是( )
A.外切 B.相交 C . 内切 D.内含
9、一个盒子中装有标号为1,2,3,4的四张卡片,采用有放回的方式取出两张卡片,下列事件中,是必然事件的是( )
A.和为奇数 B.和为偶数 C.和大于5 D.和不超过8
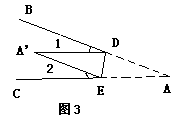 10、如图3,将∠BAC沿DE向∠BAC内折叠,使AD与A’D重合,A’E与AE重合,若∠A=300,则∠1+∠2的度数为( )
10、如图3,将∠BAC沿DE向∠BAC内折叠,使AD与A’D重合,A’E与AE重合,若∠A=300,则∠1+∠2的度数为( )
A、500 B、600 C、450 D、以上都不对
二、填空题:本大题8个小题;每小题3分,共24分.把答案写在题中横线上.
11、抛物线y=x2-1的顶点坐标是_______.
12、已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是______.
13、一个多边形的每个外角都等于30°,这个多边形的内角和为_________度.
14、圆锥的母线长为8cm,底面半径为2cm,则圆锥的表面积为___________.
15、如图7,双曲线![]() 与直线
与直线![]() 相交于A、B两点,B点坐标为(-2,-3),则A点坐标为_______________.
相交于A、B两点,B点坐标为(-2,-3),则A点坐标为_______________.
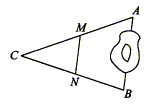
16、A、B两点被池塘隔开(如下图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=20m,则A、B两点的距离为___________.

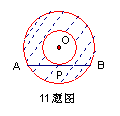
17、如图同心圆,大⊙O的弦AB切小⊙O于P,且AB=6,则阴影部分既圆环的面积为 .
18、观察下列各式:![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为
三、解答题:本大题8个小题;共46分.解答应写出文字说明、证明过程或演算步骤.
19、(每小题5分,共10分)
(1)计算:![]() (2)已知:a=2,求(1+
(2)已知:a=2,求(1+![]() )·(a2-1)值.
)·(a2-1)值.
20、(5分)如图,![]() ABC中,
ABC中,![]() ABC=
ABC=![]() BAC=
BAC=![]() ,点P在AB上,AD
,点P在AB上,AD![]() CP,BE
CP,BE![]() CP,垂足分别为D、E,已知DC=2,求BE的长.
CP,垂足分别为D、E,已知DC=2,求BE的长.

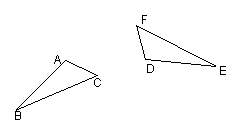
21、(5分)△DEF是由△ABC绕某点旋转得到,请画出这两个图形的旋转中心.
22、(5分)如图,已知弦AB与半径相等,连结OB,并延长使BC=OB.
(1)问AC与⊙O有什么关系.
(2)请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
23、(5分)如图7,小丽在观察某建筑物![]() .
.
(1)请你根据小亮在阳光下的投影,画出建筑物![]() 在阳光下的投影.
在阳光下的投影.
 (2)已知小丽的身高为
(2)已知小丽的身高为![]() ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物![]() 的投影长分别为
的投影长分别为![]() 和
和![]() ,求建筑物
,求建筑物![]() 的高.
的高.
24、(5分)某校需要添置某种教学仪器,有两种方案:方案1:到商家购买,每件需要8元;方案2:学校自己制作,每件4元,另外需要制作工具的租用费120元.
设需要仪器x件,方案1与方案2的费用分别为y1,y2(元).
(1)分别写出y1,y2的函数表达式.(2)当购置仪器多少件时,两种方案的费用相同?
(3)需要仪器50件,采用哪种方案便宜?请说明理由.
25、(5分)右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
(1)求该班有多少名学生?(2)补上步行分布直方图的空缺部分;
 (3)在扇形统计图中,求骑车人数所占的圆心角度数。
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有500人,估计该年级步行人数。
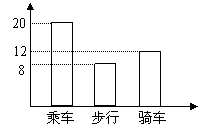 |
26、(6分)已知抛物线与x轴交于A(-1,0)和B(3,0)两点,且与y轴交于点C(0,3)。(1)求抛物线的解析式;(2)抛物线的对称轴和顶点M坐标;(3)求四边形ABMC的面积。