中考数学方案设计专题训练
1、请将四个全等的直角梯形（如图）拼成一个平行四边形，并画出两种不同的拼法示意图（拼出的两个图形只要不全等就认为是不同的拼法）
2、（甘肃）现需测量一井盖（圆形）的直径，但只有一把角尺（尺的两边．互相垂直，一边有刻度，且两边长度都长于井盖半径）．请配合图形、文字说 明测量方案，写出测量的步骤（要求写出两种测量方案）．
3、如图6，A、B两点被池塘隔开，为测量AB两点的距离，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN＝20m，那么AB＝2×20m＝40m。
（1）
测AB距离也可由图7所示用三角形相似知识来解决，请根据题意填空：延长AC到D，使CD＝
AC，延长BC到E，使CE＝________，则由相似三角形得，AB=_______.
（2）
测AB距离还可由三角形全等的知识来设计测量方案，求出AB的长，请用上面类似的方法，在图8中画出图形，并叙述你的测量方案。
 |  | ||
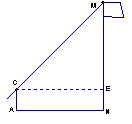4、（本题满分6分）在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：
（1） 在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；
（2） 量出测点A到旗杆底部N的水平距离AN＝m;
（3） 量出测倾器的高度AC＝h。
根据上述测量数据，即可求出旗杆的高度MN。
如果测量工具不变，请仿照上述过程，设计一个测量
某小山高度（如图2）的方案：
1） 在图2中，画出你测量小山高度MN的示意图
（标上适当的字母）
2）写出你的设计方案。
5、（陕西）在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．
⑴ 请根据下列图形，填写表中空格：
⑵ 如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？
⑶ 从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．
6、（烟台）（1）四年一度的国际数学家大会于2002年8月20日在北京召开．大会会标如图甲．它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积为13，每个直角三角形两直角边的和是5．求中间小正方形的面积．
（2）现有一张长为6.5cm、宽为2cm的纸片，如图，请你将它分割成6块，再拼合成一个正方形．（要求：先在图乙中画出分割线，再画出拼成的正方形并标明相应数据）
 | |||
 | |||
7、 两人邀去某风景区游玩, 每天某一时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度, 也不知道汽车开过来的顺序. 两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车. 而乙则是先观察后上车, 当第一辆车开来时, 他不上车, 而是子痫观察车的舒适状况, 如果第二辆车的舒适程度比第一辆好, 他就上第二辆车; 如果第二辆车不比第一辆好, 他就上第三辆车.
如果把这三辆车的舒适程度分为上、中、下三等, 请尝试着解决下面的问题:
(1) 三辆车按出现的先后顺序工有哪几种不同的可能?
(2) 你认为甲、乙采用的方案, 哪一种方案使自己乘上等车的可能性大? 为什么?
8、（生产方案的设计）某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品，共50件。已知生产一件A种产品需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元。
(1)要求安排A、B两种产品的生产件数，有哪几种方案?请你设计出来；
(2)生产A、B两种产品获总利润是y(元)，其中一种的生产件数是x，试写出y与x之间的函数关系式，并利用函数的性质说明(1)中的哪种生产方案获总利润最大?最大利润是多少?
9、（调运方案设计 ） 北京某厂和上海某厂同时制成电子计算机若干台，北京厂可支援外地10台，上海厂可支援外地4台，现在决定给重庆8台，汉口6台。如果从北京运往汉口、重庆的运费分别是4百元/台、8百元/台，从上海运往汉口、重庆的运费分别是3百元/台、5百元/台。求：
(1)若总运费为8400元，上海运往汉口应是多少台?
(2)若要求总运费不超过8200元，共有几种调运方案?
(3)求出总运费最低的调运方案，最低总运费是多少元?
10、（优惠方案的设计）某校校长暑假将带领该校市级“三好生”去北京旅游。甲旅行社说：“如果校长买全票一张，则其余学生可享受半价优待。”乙旅行社说：“包括校长在内，全部按全票价的6折(即按全票价的60%收费)优惠。”若全票价为240元。
(1)设学生数为x，甲旅行社收费为y甲，乙旅行社收费为y乙，分别计算两家旅行社的收费(建立表达式)；
(2)当学生数是多少时，两家旅行社的收费一样；
(3)就学生数x讨论哪家旅行社更优惠。
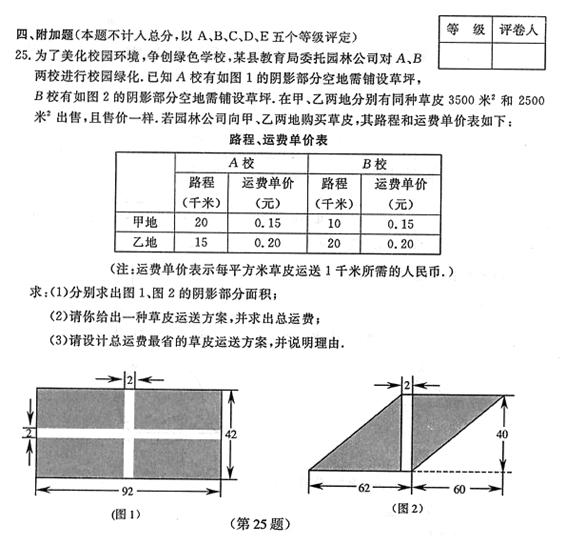
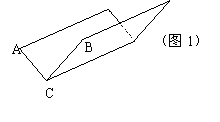
11、 下面让我们来探究有关材料的利用率问题：工人师傅要充分利用一块边长为100㎝的正三角形簿铁皮材料（如图1）来制作一个圆锥体模型（制作时接头部分所用材料不考虑）。
（1）求这块三角形铁皮的面积（结果精确到0.01㎝2）；
（2）假如要制作的圆锥是一个无底面的模型，且使三角形铁皮的利用率最高，请你在图2中画出裁剪方案的草图，并计算出铁皮的利用率（精确到1％）；
（3）假如要用这块铁皮裁一块完整的圆形和一块完整的扇形，使之配套，恰好做成一个封闭圆锥模型，且使铁皮得到充分利用，请你设计一种裁剪方案，在图3中画出草图，并计算出铁皮的利用率（精确到1％）。
 |  |  | |||
13、（应用方案设计）(2005金湖) 课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
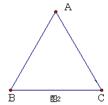
⑴方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
 |
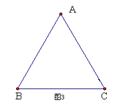
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，
并与方案①中的y的最大值比较大小．
⑵假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．