中考第二次模拟考试数学试卷
一.细心填一填(每空2分,共36分):
1. ![]() 的相反数是________, 9的平方根是________,
的相反数是________, 9的平方根是________,
2. 分解因式:x3-x =________________。
3. 中国的互联网上网用户数居世界第二位,用户已超过7880万,用科学记数法表示7880万这个数据为________万.
4. 设m,n是方程x2-4x+1=0的两个实根,则m+n=________,mn=________。
 5. 函数y=
5. 函数y=![]() 中,自变量x的取值范围是________;
中,自变量x的取值范围是________;
函数y=![]() 中,自变量x的取值范围是________。
中,自变量x的取值范围是________。
6. 已知函数y=![]() 的图象过点(-2,3),则k=_________。 (第8题)
的图象过点(-2,3),则k=_________。 (第8题)
7.已知圆锥的高是4cm,底面半径是3cm,则这个圆锥的侧面积是_________cm2 。
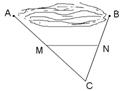
 8.如图,A、B两点被池塘隔开,在A、B外选一点C,连接AC和BC,并分别找出它们的中点M、N,若测得MN=15m,则A、B两点的距离为_________m。
8.如图,A、B两点被池塘隔开,在A、B外选一点C,连接AC和BC,并分别找出它们的中点M、N,若测得MN=15m,则A、B两点的距离为_________m。
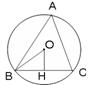
9. 如图,△ABC内接于圆O,BC=4,圆心O到BC的距离OH的长为1,
则圆O的半径为________,sinA=________。
(第9题)
10. 某校初一新生参加军训,小颖同学进行五次实弹射击的成绩(单位:环)如下:
8,6,10,7,9,则这五次射击的中位数是 环,方差是 环![]() .
.
![]()
![]() 11、如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是 .
11、如图,是正方体的一个平面展开图,在这个正方体中,与“爱”字所在面相对的面上的汉字是 .
 |
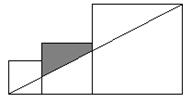
12.已知三个边长分别为3、5、7的正方形如图排列,则图中阴影部分面积为 .
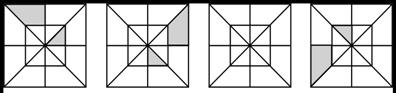 13. 分析图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
13. 分析图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.
① ② ③ ④
二.精心选一选:(每题3分,共21分):
14.以下调查适合普查的是 ( )
A.了解一批灯泡的使用寿命
B.调查全国八年级学生的视力情况
C.评价一个班级学生升学考试的成绩
D.了解无锡市的家庭人均收入
15.下列各图中,是中心对称图形的是 ( )
 |
16.下列运算中,(1)a2a3=a6 (2)(-2x2)4=16x8![]() (3)
(3)![]() (4)(a+b)(b-a)=b2-a2 其中正确的个数有
( )
(4)(a+b)(b-a)=b2-a2 其中正确的个数有
( )
A.1个 B.2个 C.3个 D.4个
17. 如图,![]() 是⊙O的两条切线,切点是
是⊙O的两条切线,切点是![]() .如果
.如果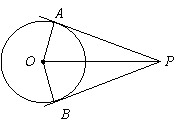
![]() ,那么∠APB等于 ( )
,那么∠APB等于 ( )
A.30° B.45°
C.60° D.90°
![]() 18.不等式组 2x>-3 的所有整数解的和是( )
18.不等式组 2x>-3 的所有整数解的和是( )
 x-1≤8-2x
x-1≤8-2x
A.0 B.2 C.5 D.6
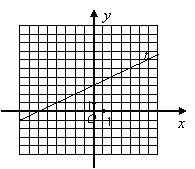
19.如图,直线![]() 是函数
是函数![]() 的图象.若点
的图象.若点![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 点的坐标可能是 ( )
点的坐标可能是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
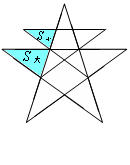
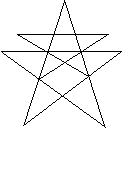 20..如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星—这一光明的象征联系在一起,那么结构图中的两个阴影三角形的面积之比
20..如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星—这一光明的象征联系在一起,那么结构图中的两个阴影三角形的面积之比![]() 为 ( )
为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
三.用心答一答:
21.(1)计算: ![]() (4分)
(4分)
(2)解方程:![]() (4分)
(4分)
22.已知,BD是平行四边形ABCD的对角线
(1) 请你用尺规作图,作出∠C、∠A的角平分线与BD交于E、F;
(2) 请你找出图中能用字母表示的所有全等的三角形,并选择一对证明之。(6分)

23.(7分)把一副普通扑克牌中的4张:黑桃2、红心3、梅花4、黑桃5,洗匀后正面朝下放在桌面上.
(1)填空:从中随机抽取一张牌是黑桃的概率是_________;
(2)小张和小英用这4张牌做游戏,游戏规定:小张先从中随机抽取一张,小英再从剩下的牌中随机抽取另一张,若这两张牌之和大于7则小英得1分,否则小张得1分。请你用表格或树状图的方法帮他们分析一下,这个游戏是否公平,并说明理由.
24.(6分)2006年无锡市春季房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷,共发放1200份调查问卷,实际收回1000份.该房地产公司根据问卷情况,作了以下两方面统计.
Ⅰ.根据被调查消费者年收入情况制成的统计表:
| 年收入(元) | 2万以下 | 2万 (不含4万) | 4万 (不含6万) | 6万 (不含8万) | 8万以上 |
| 各段被调查消费者人数占总被调查消费都人数的百分比 | 50% | 26% | 14% | 7% | 3% |
Ⅱ.根据被调查消费者打算购买不同住房面积的人数情况制成的扇形统计图:
 |
根据上述信息,解决下列问题:
(1)被调查的消费者平均年收入为 万元.(提示:在计算时,2万元以下的都看成1万元,2万![]() 4万元的都看成3万元,依此类推,8万元以上的都看成9万元)
4万元的都看成3万元,依此类推,8万元以上的都看成9万元)
(2)打算购买80![]() 100
100![]() 的消费者人数为
人.
的消费者人数为
人.
(3)如果你是该房地产公司的开发商,请你从建房面积等方面谈谈你今后的工作打算(不超过30字).
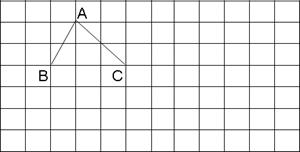
25.(4分)已知如图△ABC为格点三角形,请在所给的方格纸(图中小正方形的边长为1个单位)内,按下列要求画出相应的图形:
(1) 画一个格点三角形DEF,使△DEF∽△ABC,且相似比为![]() :1;
:1;
(2) 画一个格点三角形ABP,使S△ABP=2S△ABC;
(3) (2)中这样的格点三角形ABP一共可画________个。
26、(8分) 小东计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用,其余的钱计划买些玩具去看望市福利院的孩子们.某周日小东在商店选中了一种小熊玩具,单价是10元,按原计划买了若干个,结果他的压岁钱还余![]() ,于是小东又多买了6个小熊玩具,这样余下的钱仅是压岁钱的
,于是小东又多买了6个小熊玩具,这样余下的钱仅是压岁钱的![]() .
.
(1)问小东原计划买几个小熊玩具,小东的压岁钱共有多少元;
(2)为了保证小东购书费用不少于压岁钱的![]() ,问小东最多可比原计划多买几个小熊玩具?
,问小东最多可比原计划多买几个小熊玩具?
-
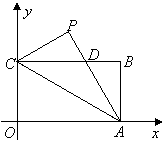
27.(8分)已知:如图,矩形![]() 的长
的长![]() ,宽
,宽![]() ,将
,将![]() 沿
沿![]() 翻折得
翻折得![]() .
.
(1)填空:![]() 度,
度,![]() 点坐标为___ _ ;
点坐标为___ _ ;
(2)若![]() 两点在抛物线
两点在抛物线![]() 上,求
上,求![]() 的值;并说明点
的值;并说明点![]() 在此抛物线上;
在此抛物线上;
(3)在(2)中的抛物线![]() 段(不包括
段(不包括![]() 点)上,是否存在一点
点)上,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,求出这个最大值及此时
的面积最大?若存在,求出这个最大值及此时![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
答案:解:(1)![]() ,
,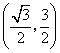 ……(2分)
……(2分)
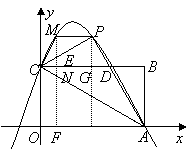
(2)![]() 点
点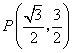 ,
,![]() 在抛物线上,
在抛物线上,

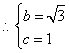
![]() 抛物线的解析式为
抛物线的解析式为![]() ……(4分)
……(4分)
![]() 点坐标为
点坐标为![]()
![]() ……(5分)
……(5分)
![]() 点在此抛物线上.
点在此抛物线上.
(3)假设存在这样的点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
![]() 面积为定值,
面积为定值,
![]() 要使四边形
要使四边形![]() 的面积最大,只需使
的面积最大,只需使![]() 的面积最大.
的面积最大.
过点![]() 作
作![]() 轴分别交
轴分别交![]() 和
和![]() 轴于
轴于![]() 和
和![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() .
.
![]()
设![]() ,
,![]()
![]()
![]()
![]() ,
,![]() 有最大值.
有最大值.
 当
当![]() 时,
时,![]() 的最大值是
的最大值是![]() ,
,
![]()
![]() 四边形
四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.
此时![]() 点的坐标为
点的坐标为 .
.
所以存在这样的点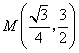 ,使得四边形
,使得四边形![]() 的面积最大,其最大值为
的面积最大,其最大值为![]() .…(8分)
.…(8分)
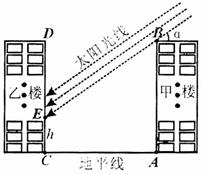
28.(8分)图①,②是燕燕同学在购新房前进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图.请你阅读相关文字,解答下面的问题.
![]()
 (1)图①是太阳光线与地面所成角度的示意图.冬至日正午时刻,太阳光线直射在南回归线(南纬23.5°)B地上.在地处北纬36.5°的A地,太阳光线与地面水平线l所成的角为
(1)图①是太阳光线与地面所成角度的示意图.冬至日正午时刻,太阳光线直射在南回归线(南纬23.5°)B地上.在地处北纬36.5°的A地,太阳光线与地面水平线l所成的角为![]() .试借助图①,求α的度数.
.试借助图①,求α的度数.
解答:(1)∵ 太阳光线是平行的,
![]() .
.
![]() .
……(2分)
.
……(2分)
(2)图②是甲楼高度、楼间距对乙楼采光影响的示意图.某小区的两幢10层住宅楼甲楼和乙楼间的距离为![]() ,由地面向上依次为第1层、第2层、
,由地面向上依次为第1层、第2层、![]() 、第10层,每层高度为
、第10层,每层高度为![]() .燕燕家的新房至少要买在乙楼的第几层,在冬至日正午时刻,采光不受甲楼的影响?若
.燕燕家的新房至少要买在乙楼的第几层,在冬至日正午时刻,采光不受甲楼的影响?若![]() 每小时增加
每小时增加![]() ,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
答:过点![]() 作
作![]() 于
于![]() ,由题意,四边形
,由题意,四边形![]() 为矩形.
为矩形.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
 又在
又在![]() 中,
中,![]() ,
,
![]() ,即
,即![]() .
.![]() .
.
(2)当![]() 时,
时,![]() ,
,
![]() ,
,![]() 点的影子落在乙楼的第五层.…… (5分)
点的影子落在乙楼的第五层.…… (5分)
因而燕燕同学家至少要买再乙楼的第6层,在冬至正午时刻,采光不受甲楼的影响。 …… (6分)
由![]() ,知
,知![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() (小时).
(小时).
故经过1小时后,甲楼的影子刚好不影响乙楼采光. ……(8分)
四、实践与探索:
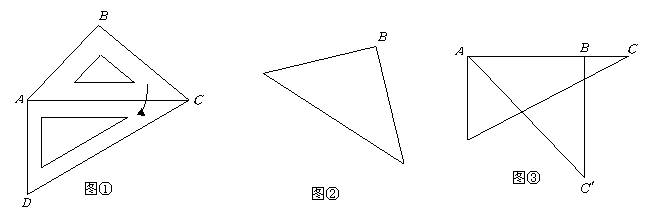
29.(9分)取一副三角板按图①拼接,固定三角板![]() ,将三角板
,将三角板![]() 绕点
绕点![]() 依顺时针方向旋转一个大小为
依顺时针方向旋转一个大小为![]() 的角
的角![]() 得到
得到![]() ,如图所示.
,如图所示.
(1)填空:当![]() 为______度时,能使得图②中
为______度时,能使得图②中![]() ;
;
(2)当旋转至图③位置,此时![]() 又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比;
又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比;
(3)连结![]() ,当
,当![]() 时,探寻
时,探寻![]() 值的大小变化情况,并给出你的证明.
值的大小变化情况,并给出你的证明.
|
|
 F
F
![]()
|
|
|
(1),![]() 时,能使得
时,能使得![]() .································································· 2分
.································································· 2分
(2)易得![]() 时,可得图③,
时,可得图③,
此时,若记![]() 与
与![]() 分别交于点
分别交于点![]() ,
,
则共有两对相似三角形:
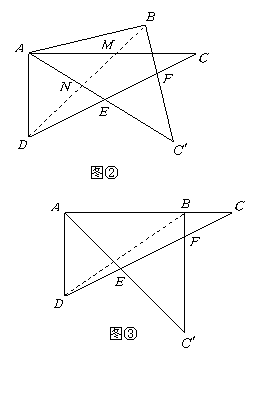
![]() .············· 4分
.············· 4分
下求![]() 与
与![]() 的相似比:
的相似比:
在图③中,设![]() ,则易得
,则易得![]() .
.
则![]()
或![]() .···································································································· 6分
.···································································································· 6分
注:![]() 与
与![]() 的相似比为:
的相似比为:![]() 或
或
![]() .
.
(3)解法一:
当![]() 时,总有
时,总有![]() 存在.
存在.
![]()
![]() ,
,
又![]() ,
,
![]() .
.
又![]() ,
,
![]() .······························································· 9分
.······························································· 9分
解法二:
在图②中,![]() 分别交
分别交![]() 于点
于点![]() ,
,
由于在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
在图③中,![]() ,
,
易得![]() ,
,
也有![]() ,
,
综上,当![]() 时,总有
时,总有![]() .·················· 9分
.·················· 9分
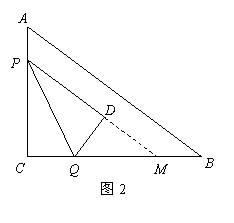
30.(9分)如图,在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以每秒
以每秒![]() 个单位长的速度运动,动点
个单位长的速度运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以每秒
以每秒![]() 个单位长的速度运动.
个单位长的速度运动.![]() 分别从点
分别从点![]() 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,
同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,![]() 关于直线
关于直线![]() 对称的图形是
对称的图形是![]() .设运动时间为
.设运动时间为![]() (秒).
(秒).
(1)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,四边形
为何值时,四边形![]() 是梯形?
是梯形?
(3)是否存在时刻![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
 (4)通过观察、画图或折纸等方法,猜想是否存在时刻
(4)通过观察、画图或折纸等方法,猜想是否存在时刻![]() ,使得
,使得![]() ?若存在,请估计
?若存在,请估计![]() 的值在括号中的哪个时间段内(
的值在括号中的哪个时间段内(![]() ;
;![]() ;
;![]() ;
;![]() );若不存在,请简要说明理由.
);若不存在,请简要说明理由.
答案:解:(1)由题意知![]() ,
,![]() ,
,
![]() .
.
![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,
![]() .……(2分)
.……(2分)
(2)当![]() 时,有
时,有![]() ,而
,而![]() 与
与![]() 不平行,这时四边形
不平行,这时四边形![]() 是梯形,
是梯形,![]() ,
,
![]() ,解得
,解得![]() .
.
![]() 当
当![]() 秒时,四边形
秒时,四边形![]() 是梯形. ……(4分)
是梯形. ……(4分)
(3)设存在时刻![]() ,使得
,使得![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,如图2,
,如图2,
若![]() ,则
,则![]() ,又
,又![]() ,
,
![]() ,从而
,从而![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
若![]() ,则
,则![]() ,得
,得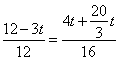 ,
,
解得![]() .
.
![]() 当
当![]() 秒时,
秒时,![]() . ……(7分)
. ……(7分)
(4)存在时刻![]() ,使得
,使得![]() .……(9分)
.……(9分)
时间段为:![]() .
.
(说明:对于(4),如果考生通过计算得到当![]() 时,
时,![]() ,也给2分)
,也给2分)