《函数》基础测试
(一)选择题(每题4分,共32分)
1.下列各点中,在第一象限内的点是………………………………………………( )
(A)(-5,-3) (B)(-5,3) (C)(5,-3) (D)(5,3)
2.点P(-3,4)关于原点对称的点的坐标是……………………………………( )
(A)(3,4) (B)(-3,-4) (C)(-4,3) (D)(3,-4)
3.若点P(a,b)在第四象限,则点Q(-a,b-4)在象限是………………( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4.函数y=![]() +
+![]() 中自变量x的取值范围是……………………………( )
中自变量x的取值范围是……………………………( )
(A)x≤2 (B)x=3 (C)x<2且x≠3 (D)x≤2且x≠3
6.若点(-m,n)在反比例函数y=![]() 的图象上,那么下列各点中一定也在此图象上的点是……………………………………………………………………………………( )
的图象上,那么下列各点中一定也在此图象上的点是……………………………………………………………………………………( )
(A)(m,n) (B)(-m,-n) (C)(m,-n) (D)(-n,-m)
7.二次函数式y=x2-2 x+3配方后,结果正确的是………………………………( )
(A)y=(x+1)2-2 (B)y=(x-1)2+2
(C)y=(x+2)2+3 (D)y=(x-1)2+4
8.若二次函数y=2 x2-2 mx+2 m2-2的图象的顶点在x 轴上,则m 的值是( )
(A)0 (B)±1 (C)±2 (D)±![]()
(二)填空题(每小题4分,共28分)
9.函数y=![]() 中自变量x 的取值范围是___________.
中自变量x 的取值范围是___________.
10.若反比例函数的图象过点(-1,2),则它的解析式为__________.
11.当m=_________时,函数(m2-m)![]() 是一次函数.
是一次函数.
12.已知一次函数y=kx+b(k≠0),当x=1时,y=3;当x=0时,y=2.则函数解析式为________,函数不经过第_____象限,y 随x 增大而________.
13.二次函数y=-x2+mx+2的最大值是![]() ,则常数m=_________.
,则常数m=_________.
14.如果二次函数y=ax2+bx+c 的图象的顶点是(-2,4),且过点(-3,0),则a为_____________.
15.若直线y=3 x+b 与两坐标轴所围成的三角形的面积为24,则b=_________.
16.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式:
 ①用水量小于等于3000吨,
;②用水量大于3000吨,
.
①用水量小于等于3000吨,
;②用水量大于3000吨,
.
(2)某月该单位用水3200吨,水费是 元;若用水2800吨,水费 元.
若某月该单位缴纳水费1540元,则该单位用水 吨.
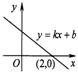
17.函数y=kx+b(k、b为常数)的图象如图所示,则关于x的不等
式kx+b>0的解集是 。
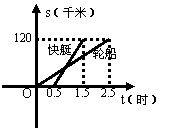 18.一艘轮船和一艘快艇沿相同路线从甲港到乙港,如图中两条线段分别表示轮船与快艇离开出发点的距离与行驶时间的关系,根据图象回答下列问题:
18.一艘轮船和一艘快艇沿相同路线从甲港到乙港,如图中两条线段分别表示轮船与快艇离开出发点的距离与行驶时间的关系,根据图象回答下列问题:
①轮船比快艇早 小时出发,快艇比轮船早到 小时;
②快艇追上轮船用 小时,快艇行驶了 千米;
③轮船从甲港到乙港行驶时间是 小时;
19.如图,![]() 表示商场一天的家电销售额与销售量的关系,
表示商场一天的家电销售额与销售量的关系,![]() 表示一天的销售成本与销售量的关系.
表示一天的销售成本与销售量的关系.
①当![]() 时,销售额= 万元,销售成本= 万元.此时,商场是是赢利还是亏损?
时,销售额= 万元,销售成本= 万元.此时,商场是是赢利还是亏损?
②一天销售 件时,销售额等于销售成本.
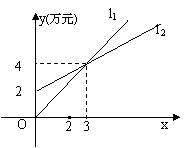 ③
③![]() 对应的函数表达式是
.
对应的函数表达式是
.
④写出利润与销售量间的函数表达式.
(三)解答题
 20.(6分)已知正比例函数的图象经过点(1,-2),求此函数的解析式,并在坐标系中画出此函数的图象.
20.(6分)已知正比例函数的图象经过点(1,-2),求此函数的解析式,并在坐标系中画出此函数的图象.
21.(8分)按下列条件,求二次函数的解析式:
(1)图象经过A(0,1),B(1,3),C(-1,1);
(2)图象经过(3,1),且当x=2时有最大值为3.
 |
22.(8分)已知二次函数y=2 x2-4 x-6.
(1)求图象的开口方向、对称轴、顶点坐标,并画出草图.
(2)求图象与x 轴的交点坐标,与y 轴的交点坐标.
(3)当x 为何值时,y 随x 的增大而增大?
(4)x 为何值时y≥0?

23、我们知道,两条直线的交点坐标就是这两直线解析式联列时所组成的方程组的解.你能据此思想对下列方程组(或方程)的解进行讨论呢?
(1)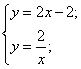 (2)
(2)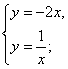 (3)
(3)![]() =2x-6.
=2x-6.
24.(8分)某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为扩大销售增加盈利,尽快减少库存,商场决定采取降价措施,经调查发现,若每件衬衫每降价1元,商场平均每天可以多售出2件.(1)若每件降价x 元,每天盈利y 元,求y 与x 的关系式.(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?(3)每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?