初中毕业生数学学业考试调研测试卷2
考生须知：
1．全卷共4页，有三大题，12小题．满分为75分，考试时间60分钟．
2．选择题做在答题卡上，填空题与解答题须做在答题卷相应位置上，做在试卷上无效．
3．请用钢笔或圆珠笔将姓名、准考证号分别填写在答卷的相应位置上．
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！
参考公式： 二次函数
图象的顶点坐标是
一、选择题（本题有5小题，每小题4分，共20分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
1.-2的相反数为( ▲ )
A．2 B．-2
C．
D． 
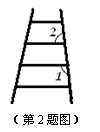
２．如图，梯子的各条横档互相平行，若∠1＝110°，
则∠2的度数为（ ▲ ）
A．50° B．70° C．90° D．110°
３．据统计：2006年义乌外贸出口金额为134067万美元，比上年增长22.76%.用科学记数法表示134067应记为（ ▲ ）
A．134.067×103 B. 13.4067×104 C. 1.34067×105 D. 0.134067×106
４． 某电视台综艺节目接到热线电话1600个,现要从中抽取“幸运观众”16名,小红打通了一次热线电话,那么她成为“幸运观众”的概率为（ ▲ ）
A．
B.
C.
D.
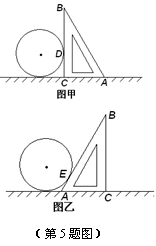
５.课题学习小组的同学接受了测量一种圆柱形工件直径的任务，他们使用的工具是一个锐角为 600的直角三角板和一把刻度尺.小明的测量方法如图甲，测得DC=9cm. 点D为切点.小亮的测量方法如图乙，点E为切点.假设他们的测量结果都是正确的.则与EA的长最接近的是( ▲ )
A.8cm B.7cm C.6cm D.5cm
二、填空题 (本题有3小题,每题5分,共15分)
6. 若反比例函数
的图象过点（
，-2），则等于 ▲ ．
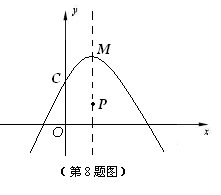7.如图,四边形ABCD为平行四边形,点E、点F分别是AB、CD上的点.请你增加一个条件，使得四边形DEBF成为平行四边形.你增加的条件是： ▲ ．(要求不标注新的字母，不添加新的线段.)
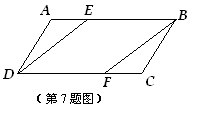
8. 如图，抛物线的顶点M的坐标是（1，3），且与y轴相交于点C（0，2），P（1，1）是抛物线对称轴上的一点.
(1)：写出抛物线解析式 ▲ （答对得3分）;
(2)：点Q是抛物线上的一点，且使ΔCPQ的面积等于ΔCMP的面积，则所有满足条件的点Q的个数为： ▲ （答对得2分）.
三、解答题 (本题有4小题,共40分,除10（1) 、11(1)、12(2) 外各小题都必须写出解答过程)
9. (本题8分)
(1)计算： 
（2）解方程：
.
10. (本题8分)
每年的6月6日是全国的爱眼日，让我们行动起来，爱护我们的眼睛！某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查，下图是利用所得数据绘制的频数分布直方图（视力精确到0.1）.请你根据此图提供的信息，回答下列问题：
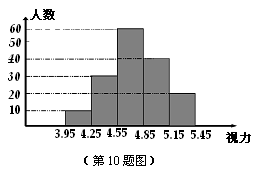
（1）本次调查共抽测了 名学生；
（2）视力在4.9及4.9以上的同学约占全校学生比例为多少？
（3）如果视力在第1，2，3组范围内(视力在4.9以下)均属视力不良，应给予治疗、矫正.请计算该校视力不良学生约有多少名？
11. (本题10分)
小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.
（1）如图（1），垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .
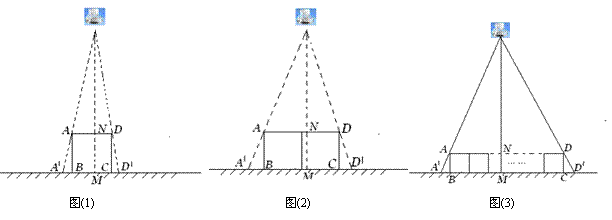
（2）不改变（1）中灯泡的高度，将两个边长为30cm的正方形框架按图（2）摆放，请计算此时横向影子A′B，D′C的长度和为多少？
（3）有n个边长为a的正方形按图（3）摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）
12.(本题14分)
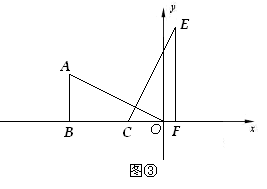
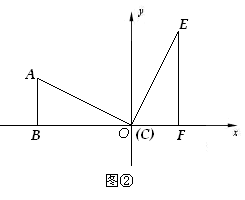
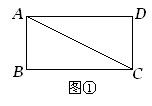
如图①，矩形ABCD被对角线AC分为两个直角三角形，AB=3，BC=6.现将Rt△ADC绕点C顺时针旋转90º，点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点，以BC所在直线为
轴，以过点C垂直于BC的直线为
轴，建立如图②的平面直角坐标系.
（1） 求直线AE的解析式；
（2） 将Rt△EFC沿轴的负半轴平行移动，如图③.设OC=（
），Rt△EFC与Rt△ABO的重叠部分面积为s；
①
当=1与=8时,求s的值；
②
S是否存在最大值？若存在，求出这个最大值及此时的值；若不存在，请说明理由．
