2004年中考复习之相似形的综合运用（一）
知识考点：
会综合运用相似三角形的有关概念、定理解答有关问题。另外，直角三角形被斜边上的高分成的两个直角三角形与原三角形相似的性质运用，是近几年中考的热点题型。
精典例题：
【例1】如图，已知，在边长为1的正方形ABCD的一边上取一点E，使AE＝
AD，从AB的中点F作HF⊥EC于H。
（1）求证：FH＝FA；
（2）求EH∶HC的值。
证明：（1）连结EF，FC，在正方形ABCD中，AD＝AB＝BC，∠A＝∠B＝900
∵AE＝AD，F为AB的中点，∴
∴△EAF∽△FBC，∴∠AEF＝∠BFC，∠EFA＝∠CFB
∴∠EFC＝900，
又∵∠EFC＝∠B＝900 ∴△EFC∽△FBC
∴∠HEF＝∠BFC，∠ECF＝∠BCF
∴∠AEF＝∠HEF，∠AFE＝∠HFE
∴△EAF≌△HEF ∴FH＝FA
（2）由（1）得，由（1）易证△EHF∽△EFC，从而可得
，同理
，于是EH∶HC＝
∶
＝1∶4
变式：如图，在矩形ABCD中，
，点E在BC上，点F在CD上，且EC＝
BC，FC＝
CD，FG⊥AE于G，。求证：AG＝4GE。
（提示：证△ECF∽△FDA得EF∶AF＝1∶2，再证△EFG∽△EAF∽△FAG即可）
【例2】已知，在△ABC中，∠ACB＝900，过C作CD⊥AB于D，AD＝
，BD＝
，
∶
＝2∶1，又关于
的方程
的两实数根的差的平方小于192，求整数、的值。
分析：如图，易证△ABC∽△ADC，∶＝AD∶BD＝∶＝2∶1，即
，再由方程两根差的平方小于192可得
，又由判别式△≥0知≤2
∴
＜≤2，又为整数，∴＝1，2
∴＝2，＝1或＝4，＝2
探索与创新：
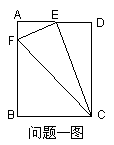
【问题一】已知：如图，在矩形ABCD中，E为AD的中点，EF⊥ EC交AB于F，连结FC（AB＞AE）。
（1）△AEF与△EFC是否相似，若相似，证明你的结论；若不相似，请说明理由。
（2）设
＝
，是否存在这样的值，使得△AEF与△BFC相似，若存在，证明你的结论并求出的值；若不存在，说明理由。
解：（1）相似，如图
证明：延长FE与CD的延长线交于点G。在Rt△AEF与Rt△DEG中
∵E是AD的中点
∴AE＝ED，∠AEF＝∠DEG，∠A＝∠EDG
∴△AFE≌△DGE
∴E为FG的中点。又CE⊥FG，∴FC＝GC ∴∠CFE＝∠G。∴∠AFE＝∠EFC，又△AEF与△EFC均为直角三角形
∴△AEF∽△EFC。
（2）①存在。如果∠BCF＝∠AEF，即＝
时，△AEF∽△BCF。
证明：当
时，
。∴∠ECG＝300。∴∠ECG＝∠ECF＝∠AEF＝300，∴∠BCF＝900－600＝300。又△AEF和△BCF均为直角三角形。∴△AEF∽△BCF。
②因为EF不平行于BC，∴∠BCF≠∠AFE。∴不存在第二种相似情况。
跟踪训练：
一、填空题：
1、在Rt△ABC中，∠BAC＝900，AD⊥BC于D，AB＝2，DB＝1，则DC＝ ，AD＝ 。
2、在△ABC中，AB＝12，AC＝15，D为AB上一点，BD＝
AB，在AC上取一点E，得△ADE，当AE的长为
时，图中的两个三角形相似。
3、在Rt△ABC中，AD为斜边上的高，
，则AB∶BC＝ 。
二、选择题：
在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，CD⊥AB于D，AB＝
，则DB＝（ ）
A、
B、
C、
D、
三、解答题：
1、如图，在△ABC中，∠ACB＝900，CD⊥AB于D，为了求出AC，在图中你能找出哪些适当的条件？
2、如图，CD是Rt△ABC的斜边AB上的高，E是BC上任意一点，EF⊥AB于F。求证：
。
3、如图，在Rt△ABC中，CD是斜边AB上的高，点M在CD上，DH⊥BM且与AC的延长线交于点E。求证：
（1）△AED∽△CBM；
（2）
4、已知，如图，在Rt△ABC中，∠ACB＝900，AD平分∠CAB交BC于点D，过点C作CE⊥AD，垂足为E，CE的延长线交AB于点F，过点E作EG∥BC交AB于点G，
，
，求EG的长。
跟踪训练参考答案
一、填空题：
1、3，
；2、10或
；3、1∶2；
二、选择题：A
三、解答题：
1、AD、DC；AB、BC；AD、AB；AD、BD；AB、BD；CD、BD；BD、BC；BC、CD；AD、BC；AB、CD等。
2、由△ADC∽△ACB得
，又由△ACD∽△EBF得
，所以
3、略
4、4