天门市2006年中考数学试卷
注意事项如下：
01．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页，满分120分，考试时间120分钟。
02．答第Ⅰ卷前，考生务必用钢笔（圆珠笔）将自己的姓名，用2B铅笔将准考证号、考试科目写或涂在答题卡上。
03．第Ⅰ卷每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动，用4B橡皮擦干净后，再涂选其它答案。答案写在第Ⅰ卷上无效。
04．答第Ⅱ卷时，将答案直接写在试卷上。
05．考试结束，考生须将第Ⅰ卷、第Ⅱ卷、答题卡一并交回。
第Ⅰ卷（选择题，共36分）
一、 选择题（本大题共12小题，每小题3分，共36分）
01．举世瞩目的三峡大坝于2006年5月20日胜利封顶。坝体混凝土浇筑量约为2643万m3，将这一数据用科学记数法表示为
A、2.643×103m3 B、0.2643×108m3 C、26.43×106m3 D、2.643×107m3
02．方程x(x+3)=(x+3)的根为
A、x1=0，x2=3 B、x1=0，x2=－3 C、x=0 D、x=－3
03．如下图a，边长为a的大正方形中一个边长为b的小正方形，小明将图a的阴影部分拼成了一个矩形，如图b。这一过程可以验证
A、a2+b2-2ab=(a-b)2; B、a2+b2+2ab=(a+b)2; C、2a2-3ab+b2=(2a-b)(a-b); D、a2-b2=(a+b) (a-b)
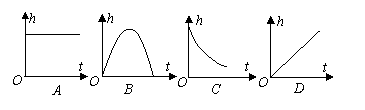
04．足球守门员大脚开出去的球的高度随时间的变化而变化，这一过程可近似地用下列那幅图刻画
05．如图，数轴上所表示的不等式组的解集是
A、x≤2 B、－1≤x≤2 C、－1＜x≤2 D、x＞－1
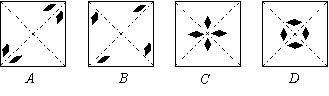
06．将正方形纸片两次对折，并剪出一个菱形小洞后铺平，得到的图形是
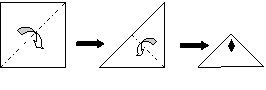
07．在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴的正方向的夹角为α，则用[ρ，α]表示点P的极坐标。显然，点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1，1)的极坐标为P[
，45°]，则极坐标Q[
，120°]的坐标为
A、(－
，3) B、(－3， ) C、(，3) D、(3， )
08．点E是
ABCD的边BC延长线上的一点，AE与CD相交于G，则图中相似三角形共有
A、2对 B、3对 C、4对 D、5对
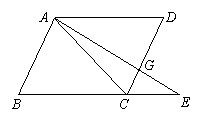
09．学校快餐店有2元，3元，4元三种价格的饭菜供师生选择（每人限购一份）。右图是某月的销售情况统计图，则该校师生购买饭菜费用的平均数和众数是
A、2.95元，3元 B、3元，3元 C、3元，4元 D、2.95元，4元
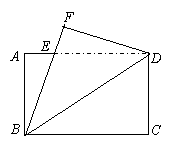
10．如图，将矩形ABCD沿对角线BD折叠，使C落在F处，BF交AD于E，则下列结论不一定成立的是
A、△ABE∽△CBD B、∠EBD=∠EDB C、AD=BF D、sin∠ABE=
11．如图，5个边长为1cm的立方体摆在桌子上，则露在表面的部分的面积为
A、13cm2 B、16cm2 C、20cm2 D、23cm2
12．老师出示了小黑板上的题后(如图)，小华说：过点(3，0)；小彬说：过点(4，3)；小明说：a=1；小颖说：抛物线被x轴截得的线段长为2。你认为四人的说法中，正确的有
A、1个 B、2个 C、3个 D、4个
第Ⅱ卷（非选择题，共84分）
二．填空题（本题有4个小题，每小题4分，共16分）
13．从标有1，3，4，6，8的五张卡片中随机抽取两张，和为奇数的概率是 。
14．观察下列各式：0，x，x2，2x3，3x4，5x5，8x6，……。试按此规律写出的第10个式子是 。
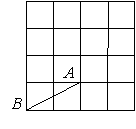
15．在方格纸上，每个小格的顶点叫格点，以格点为顶点的三角形叫格点三角形。如图，在4×4的方格纸上，以AB为边的格点三角形ABC的面积为2个平方单位，则符合条件的C点共有 个。
16．Rt△ABC中，∠ABC=90°，D是AC中点，⊙O经过A、B、D三点，CB的延长线交⊙O于E，连接AE、OD。根据以上条件，写出四个正确的结论。（半径相等及勾股定理结论除外，且不得添加辅助线）
① ② ③ ④
三．解答题（本大题共8个小题，共68分）
17．（本小题满分6分）计算：－22＋
＋(π－1)0－3×
18．（本小题满分7分）先化简，再求值：
，其中
19．（本小题共2个小题，其中第(1)小题3分，第(2)小题4分，满分7分）
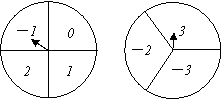
（1）如图所示的转盘中指针落在每个数字上的机会相等，现同时转动A、B两转盘，停止后，指针各指向一个数字。小彬和小颖利用这个转盘做游戏：若两数之积为非负数则小彬胜，否则，小颖胜。你认为这个游戏对双方公平吗？ （直接写出结果）
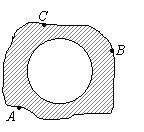（2）小明在操场上做游戏，他发现地上有一个不规则的封闭图形ABC。为了知道它的面积，小明在封闭图形内划出了一个半径为1米的圆，在不远处向圈内掷石子，且记录如下：
|
| 50次 | 150次 | 300次 |
| 石子落在⊙O内(含⊙O上)的次数m | 14 | 43 | 93 |
| 石子落在阴影内的次数n | 19 | 85 | 186 |
你能否求出封闭图形ABC的面积？试试看。
20．本小题有2个小题，请你从中任选一题作答，如两题都作答，按解答完整的题给分（本题满分7分）
测量路灯的高度或河的宽度。
说明：①测量可以在有阳光的晴日里进行。
②测量者手头只有若干个标竿及测量长度的皮尺。
③画出相关图形，用a、b、c……等表示测量所得的数据。
题（1）小明和爸爸一起散步，发现小区新安装了漂亮的路灯。决定测量一下路灯的高度。请你帮小明设计一个测量方案。
题（2）小彬星期天到郊外游玩，来到一条不能到达对岸的河边，决定测量一下小河的宽度(河岸大致平行)。请你帮助小彬设计一个测量方案。
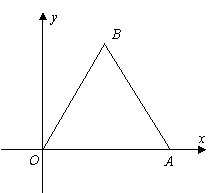
21．（本小题满分8分）如图，边长为2的等边三角形OAB的顶点A在x轴的正半轴上，B点位于第一象限。将△OAB绕点O顺时针旋转30°后，恰好点A落在双曲线
上。（1）求双曲线的解析式；（2）等边三角形OAB继续按顺时针旋转多少度后，A点再次落在双曲线上？
22．（本小题满分10分）
我们把能平分四边形面积的直线称为“好线”。利用下面的作图，可以得到四边形的“好线”：在四边形ABCD中，取对角线BD的中点O，连结OA、OC。显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”。
（1）试说明直线AE是“好线”的理由；
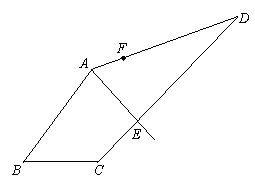
（2）如下图，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，并对画图作适当说明(不需要说明理由)。
23．（本小题满分10分）
某地为促进特种水产养殖业的发展，决定对甲鱼和黄鳝的养殖提供政府补贴。该地某农户在改建的10个1亩大小的水池里分别养殖甲鱼和黄鳝，因资金有限，投入不能超过14万元，并希望获得不低于10.8万元的收益，相关信息如下表所示：（收益=毛利润—成本＋政府补贴）
| 养殖种类 | 成本(万元/亩) | 毛利润(万元/亩) | 政府补贴(万元/亩) |
| 甲鱼 | 1.5 | 2.5 | 0.2 |
| 黄鳝 | 1 | 1.8 | 0.1 |
（1）根据以上信息，该农户可以怎样安排养殖？
（2）应怎样安排养殖，可获得最大收益？
（3）据市场调查，在养殖成本不变的情况下，黄鳝的毛利润相对稳定，而每亩甲鱼的毛利润将减少m万元。问该农户又该如何安排养殖，才能获得最大收益？
24．（本小题满分13分）
直线l的解析式为
，与x轴、y轴分别交于A、B两点，P是x轴上一点，以P为圆心的圆与直线l相切于B点。
（1）求点P的坐标及⊙P的半径R；
（2）若⊙P以每秒
个单位沿x轴向左运动，同时⊙P的半径以每秒
个单位变小，设⊙P的运动时间为t秒，且⊙P始终与直线l有交点，试求t的取值范围；
（3）在(2)中，设⊙P被直线l截得得弦长为a，问是否存在t的值，使a最大？若存在，求出t的值；
（4）在(2)中，设⊙P与直线l的一个交点为Q，使得△APQ与△ABO相似，请直接写出此时t的值。