浙江省湖州市2004年高中段招生统一考试
数学试卷
一、选择题(本题有10小题,每小题3分,共30分)
1、2的倒数是( )
A、1/2 B、-1/2 C、-2 D、0.2
2、正方形是轴对称图形,它的对称轴共有( )
A、2条 B、3条 C、4条 D、6条
3、抛物线y=2(x-3)2的顶点在( )
A、第一象限 B、第二象限 C、x轴上 D、y轴上
4、圆柱的底面半径为5cm,高为12cm,则该圆柱的侧面积等于( )
A、60cm2 B、60πcm2 C、120cm2D、 120πcm2
 5、如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为( )
5、如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为( )
A、4 B、16 C、2![]() D、4
D、4![]()
6、已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1O2=7cm,则⊙O1与⊙O2的位置关系为( )
A、外离 B、外切 C、内切 D、相交
7、已知一元二次方程x2+3x-4=0的两个根为x1、x2,则x1·x2的值是( )
A、4 B、-4 C、3 D、-3
 8、方程组
8、方程组 的解是( )
的解是( )
![]()
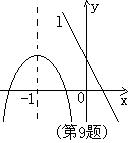
9、已知抛物线和直线ι在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线ι上的点,且-1<x1<x2,x3<-1则y1,y2,y3的大小关系为( )
 A.
y1<y2<y3 B.
y3<y1<y2
A.
y1<y2<y3 B.
y3<y1<y2
C. y3<y2<y1 D. y2<y1<y3
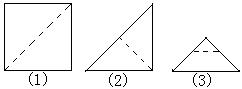
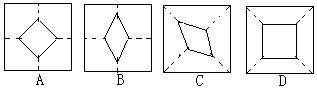 10、小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )
10、小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )
二、填空题(本题有10分,每小题3分,共30分)
11、-1的相反数是_______。
12、已知x:y=1:2,则(x+y):y=_______。
 13、在平面直角坐标系中,点(3,-5)在第_______象限。
13、在平面直角坐标系中,点(3,-5)在第_______象限。
14、当x_______时,分式![]() 无意义。
无意义。
15、已知双曲线y=![]() 经过点(1,-2),则k的值等于___
经过点(1,-2),则k的值等于___
16、分解因式:ax2-ay2=_______
 17、已知梯形的中位线长为6,下底长为9,则该梯形上底的长为_______
17、已知梯形的中位线长为6,下底长为9,则该梯形上底的长为_______
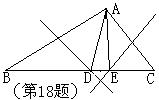
18、已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于_______
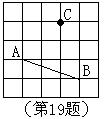
19、如图,已知图中每个小方格的边长为1,则点C到AB所在直线的距离等于_______
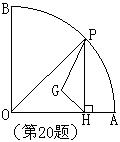 20、如图,在半径为9,圆心角为90°的扇形OAB的弧AB上有一动点P,PH⊥OA,垂足为H,设G为△OPH的重心(三角形的三条中线的交点),当△PHG为等腰三角形时,PH的长为_______
20、如图,在半径为9,圆心角为90°的扇形OAB的弧AB上有一动点P,PH⊥OA,垂足为H,设G为△OPH的重心(三角形的三条中线的交点),当△PHG为等腰三角形时,PH的长为_______
三、解答题(本题有6小题,共60分)
21、(本题9分)计算:(-1)0+![]()
22、(本题9分)解方程:![]()
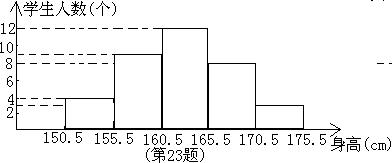
23、(本题10分)某校初三(1)班36位同学的身高的频数分布直方图如图所示。问:(1)身高在哪一组的同学最多?(2)身高在160cm以上的同学有多少人?(3)该班同学的平均身高约为多少(精确到0.1cm)?
 24、(本题10分)已知如图,直线y=-2x+2与x轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D。(1)求点A、B的坐标和AD的长;
24、(本题10分)已知如图,直线y=-2x+2与x轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D。(1)求点A、B的坐标和AD的长;
(2)求过B、A、D三点的抛物线的解析式。
25、(本题11分)织里某童装加工企业今年五月份工人每天平均加工童装150套,最不熟练的工人加工的童装套数为平均套数的60%。为了提高工人的劳动积极性,按时完成外贸订货任务,企业计划从六月份起进行工资改革。改革后每位工人的工资分二部分:一部分为每人每月基本工资200元;另一部分为每加工1套童装奖励若干元。
(1)为了保证所有工人的每月工资收入不低于市有关部门规范的最低工资标准450元,按五月份工人加工的童装套数计算,工人每加工1套童装企业至少应奖励多少元(精确到分)?
 (2)根据经营情况,企业决定每加工1套童装奖励5元。工人小张争取六月份工资不少于1200元,问小张在六月份应至少加工多少套童装?
(2)根据经营情况,企业决定每加工1套童装奖励5元。工人小张争取六月份工资不少于1200元,问小张在六月份应至少加工多少套童装?
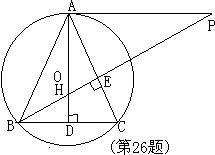
26、(本题11分)如图,H是⊙O的内接锐角△ABC的高线AD、BE的交点,过点A引⊙O的切线与BE的延长线相交于点P,若AB的长是关于x的方程x2-6![]() x+36(cos2c-cosc+1)=0的实数根。
x+36(cos2c-cosc+1)=0的实数根。
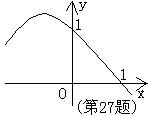 (1)求:∠C=_______度;AB的长等于_______(直接写出结果)
(1)求:∠C=_______度;AB的长等于_______(直接写出结果)
(2)若BP=9,试判断△ABC的形状,并说明理由。
四、自选题(本题有2个小题,共10分)
注意:本题为自选题,供考生选做,自选题得分将记入本学科的总分,但考生所得总分最多为120分)。
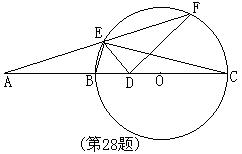 27、(本题4分)二次函数y=ax2+bx+c的图象的一部分如图所示,则a的取值范围是_______
27、(本题4分)二次函数y=ax2+bx+c的图象的一部分如图所示,则a的取值范围是_______
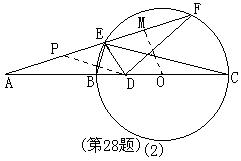
28、(本题6分)已知如图所示,A是⊙O的直径CB延长线上一点,BC=2AB,割线AF交⊙O于E、F,D是OB的中点,且DE⊥AF,连结BE、DF。
(1)试判断BE与DF是否平行?并说明理由;(2)求AE:EC的值。
参 考 答 案
一、选择题(本题有10小题,每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | D | A | D | B | B | D | D |
二、填空题(本题有10分,每小题3分,共30分)
11、1;
12、3:2; 13、四; 14、=5;
15、-2; 16、a(x+y)(x-y);17、3; 18、8; 19、![]() ;
20、3或
;
20、3或![]() 。
。
三、解答题(本题有6小题,共60分)
21、解:原式=1+2![]() +
+![]() -1……6分 =3
-1……6分 =3![]() ………………3分
………………3分
22、解:支分母得:2(1+x)-(1-x2)=1-x…………2分
化简得:x2+3x=0……………………1分
解得:x1=0,x2=-3………………4分
经检验:x1=0,x2=-3都是原方程的根…………1分
∴原方程的根为x1=0,x2=-3……………………1分
23、解(1)身高在160.5~165.5cm这一组人数最多。…………3分
(2)身高在160cm能上能下的同学有23人……………3分
(3)该班同学的平均身高为:
![]() =162.6(cm)……4分
=162.6(cm)……4分
24、解:(1)由题设可得A(1,0),B(0,2)…………………4分
在△ABO和△CAD中,∵∠BAC=90°,
∴∠ABO=∠CAD=90°-∠OAB,又AB=AC,
∴Rt△ABO≌Rt△CAD………………………………1分
∴AD=BO=2……………………………………………1分
(2)设经过A、B、D三点的抛物线的解析式为y=a(x-m)(x-n)
由(1)可得:D点坐标为(3,0),又A(1,0),B(0,2)
∴ ………………3分
………………3分
∴所求解析式为y=![]() (x-1)(x-3),即y=
(x-1)(x-3),即y=![]() x2-
x2-![]() x+2……1分
x+2……1分
25、解(1)设企业每套奖励x元………………………………1分
由题意得:200+60%·150x≥450…………………2分
解得:x≥2.78………………………………………2分
因此该企业至少应奖励2.78元……………………1分
(2)设小张在六月份加工y套
由题意得:200+5y≥1200…………………………2分
解得:y≥200………………………………………2分
答:小张在六月份应至少加工200套。……………………1分
26、(1)60°…………3分; 3![]() ………………3分
………………3分
(2)结论:△ABC是等边三角形…………1分
∵AD、BE是△ABC的高, ∴∠P+∠PAC=∠BAD+∠ABC=90°
又PA切⊙O于A,∴∠PAC=∠ABC,∴∠P=∠BAD而∠PBA=∠ABH,
△PBA∽△ABH,∴![]() ,∴当PB=9时,BH=
,∴当PB=9时,BH=![]() =3……2分
=3……2分
在Rt△BHD中,BD=BH·cos30°=![]() …………………1分
…………………1分
在Rt△ABD中,cos∠ABD=![]() ,∴∠ABD=60°
,∴∠ABD=60°
即∠ABC=60°………………………………………………1分
∵∠C=60°,∴△ABC是等边三角形。
四、自选题(本题有2个小题,共10分)
27、-1<a<0……………………4分(评分标准:全对得满分,否则不得分。)
28、(1)BE与DF不平行…………………………………………1分
过O作OM⊥EF,垂足为M,则ME=MF,
∵DE⊥AE,∴DE∥OM,∴AE:AM=AD:AO=3:4……1分
∴AE:AF=3:5
∵AB:AD:2:3,∴AE:AF≠AB:AD…………1分
∴BE与DF不平行。
(2)取AE的中点P,连DP交BE于Q,
∵D是AC的中点,P是AE的中点,∴DP∥CE,
∵BE⊥EC,∴BE⊥DQ
由DQ∥CE得![]()
 ∴DP=2DQ即DQ=PQ又BE⊥DP
∴DP=2DQ即DQ=PQ又BE⊥DP
∴BE是DP的中垂线
∴EP=ED………………………2分
∵∠AED=Rt∠
∴△EDP为等腰Rt△
∴DP=![]() EP
EP
∴AE:EC=2EP:2DP=1:![]() …1分
…1分