2005年中考数学复习同步检测（18） 姓名
（三角形2）
一．填空题：
1．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，
这样做的道理是 ．
2．如图，△ABD≌△ABC，∠C＝100°，∠CBD＝30°，那么
∠DAB＝ °；
3．直角三角形中，两锐角之比为
，则两锐角的度数
分别为 ；
4．完成下面的推理：如图，
（1）在△ABC与△A’B’C’中，
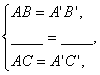
∴△ABC≌△A’B’C’(SAS)．
（2）在△ABC与△A’B’C’中，
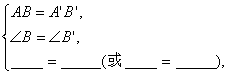
∴△ABC≌△A’B’C’(AAS)．
5．在△ABC与△A’B’C’中，AB＝A’B’，∠A＝∠A’，要说明△ABC≌△A’B’C’，还需要增加条件
；
6．AD是⊿ABC的中线。⊿ABD的周长比⊿ADC的周长大4，
则AB与AC的差为_________；
7．如右图，已知∠A =∠C，要证明⊿AOB≌⊿COD,根据
“ASA”还要一个条件__________；
8．如图2，沿AM折叠，使D点落在BC上的N点处，如果AD=7cm，
DM=5cm，∠DAM=300，则AN= cm，NM = cm，∠NAM= ；
9．如图3，△ABC≌△AED，∠C=400，∠EAC=300，∠B=300，则
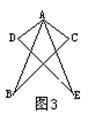∠D= ，∠EAD= ；
10．已知 , 如图 ,
∠A=∠D=90°,
BE=CF , AC=DE , 则△ABC≌___ __；
二．选择题：
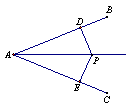11．如图，PD⊥AB，PE⊥AC，垂足分别为D、E，且PD＝PE，则△APD与△APE全等的理由是
（ ）
A SAS B AAS
C SSS D HL
12．如果在△ABC中，∠A＝70°－∠B，则∠C等于 （ ）
A 35° B 70° C 110° D 140°
13．下列说法错误的是 （ ）
A 三角形三条中线交于一点 B 三角形三条角平分线交于一点
C 三角形三条高交于一点 D 三角形中线、角平分线、高都是线段
14．在下列条件中，不能说明△ABC≌△A’B’C的是 （ ）
A ∠A＝∠A’，∠C＝∠C’，AC＝A’C’ B ∠A＝∠A’，AB＝A’B’，BC＝B’C’
C ∠B＝∠B’，∠C＝∠C’，AB＝A’B’ D AB＝A’B’， BC＝B’C，AC＝A’C’
15．在下列说法中，正确的有 （ ）
①三角对应相等的两个三角形全等；②三边对应相等的两个三角形全等；③两角、一边对应相等的两个三角形全等；④两边、一角对应相等的两个三角形全等；
A 1条 B 2条 C 3条 D 4条
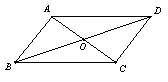
16．如图，AB∥CD，AD∥BC，AC与BD相交于点O，
则图中全等的三角形有 （ ）
A 1对 B 2对 C 3对 D 4对
17．在下列条件中：①∠A+∠B=∠C，②∠A∶∠B∶∠C=1∶2∶3，③∠A=900－∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有 （ ）
A 1个 B 2个 C 3个 D 4个
18．如果一个三角形的三条高所在直线的交点在三角形外部，那么这个三角形是 （ ）
A 锐角三角形 B 直角三角形 C 钝角三角形 D 等边三角形
19．若⊿ABC≌⊿DEF那AC的对应边是 （ ）
A DE B DF C EF D BC
20．如图加条件能满足AAS来判断⊿ACD≌⊿ABE的条件是
（ ）
A ∠AEB = ∠ADC ∠C = ∠D
B ∠AEB = ∠ADC CD = BE
C AC = AB AD = AE
D AC = AB ∠C =∠B
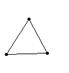
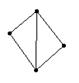
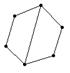
21．下列由几根木条用钉子钉成如下的模型，其中在同一平面内不具有稳定性的是 （ ）
 |  |  | |||||
 | |||||||
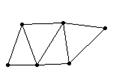A B C D
22．两个直角三角形全等的条件是 （ ）
A 一个锐角对应相等 B 两个锐角对应相等 C 一条边对应相等 D 两条边对应相等
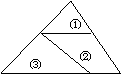23．如图，某人不小心把一块三角形的玻璃打碎成三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是
（ ）
A 带①去 B 带②去
C 带③去 D 带①和②去
24．下列命题中不正确的是 （ ）
A. 全等三角形的对应高相等 B. 全等三角形的面积相等
C. 全等三角形的周长相等 D. 周长相等的两个三角形全等
三．解答题：
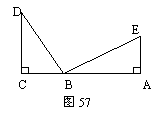25．如图，DC⊥CA，EA⊥CA，DB⊥EB，DB=BE，
（1）△BCD与△EAB是否全等？为什么？
解：∵DC⊥CA，EA⊥CA，DB⊥EB (已知)
∴∠C=∠A=∠DBE=90° ( )
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中，∠DBC+∠D=90°( )
∴∠D=∠EBA ( )
在△BCD与△EAB中
∠D=∠EBA （已证）
∠C= （已证）
DB= （已知）
∴△BCD≌△EAB ( )
（2）你能说明AC = CD + AE吗？
26．如图，已知AB＝AC，BD＝CE。求证：△ABE≌△ACD；
 |
27．已知：如图DC⊥CA，EA⊥CA，CD＝AB，CB＝AE，求证：△BCD≌△EAB
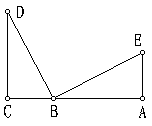
28． 已知：如图，AE＝CF，∠DAF＝∠BCE，AD＝CB。问：△ADF与△CBE全等吗？请说明理由。
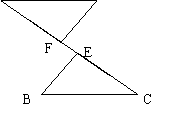
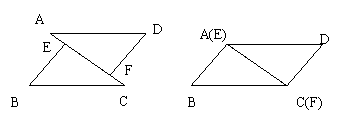
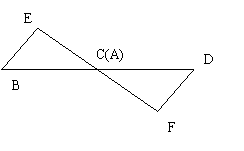29．如果将△BEC沿CA边方向平行移动，可有下列３幅图，如上面的条件不变，结论仍成立吗？请说明理由。
 |