1.已知
，则代数式
的值是
A．
B．
C．
D．
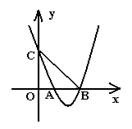
2．如图，抛物线
与
轴交于
、
两点，与
轴交于点
，
，则下列各式成立的是
A．
B．
C．
D．
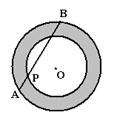
3．如图，两同心圆间的圆环（即图中阴影部分）的面积为
，过小圆上任一点
作大圆的弦
，则
的值是
A．
B． C．
D．
4．如图，△
是锐角三角形，正方形
的一边在
上，其余两个顶点分别在、
上．记△的面积为
，正方形的面积为
，则有
A．≥2
B．≤2
C．＞2
D．＜2
5.图1是一个三角形，分别连结这个三角形的中点得到图2；再分别连结图2中间的小三角形的中点，得到图3，按此方法继续下去，请你根据每个图中三角形个数的规律，完成下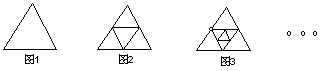
列问题：
（1）将下表填写完整：
| 图形编号 | 1 | 2 | 3 | 4 | 5 | … |
| 三角形个数 | 1 | 5 | 9 |
|
| … |
（2）在第n个图形中有 个三角形（用含n的式子表示）
6.有一块方角形钢板如右图所示，请你用一条直线将其分为面积相等的两部分（不写作法，保留作图痕迹，在图中直接画出）
7.已知半径为4和 
的两圆相交，公共弦长为4，则两圆的圆心距为
8.如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2米的汤姆沿着地球赤道环行一周，他的头顶比脚底多行_______米。
9．若│x│+3=│x-3│,则x的取值范围是____________.
10. 已知关于的不等式组
无解，则
的取值范围是 。
11. 古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，
它有一定的规律性，则第24个三角形数与第22个三角形数的差为
。
12. 观察一列数：3，8，13，18，23，28……依次规律，在此数列中比2000大的数最小整数是 ；
13. CD是Rt△ABC斜边上的高线，AD、BD是方程x2－6x+4=0的两根，则△ABC的面积为 ；
14. 如图，平面镜A与B之间夹角为120°，光线经平面镜A反射在平面镜B上，再反射出去，若∠1=∠2，则∠1= ；
15.如图所示的某种玩具是由两个正方体用胶水粘合而成的，它们的棱长
分别为1分米和2分米.为了美观，现要在其表面喷涂油漆，已知喷涂
1平分分米需用油漆5克，那么喷涂这个玩具共需油漆 克.
16. 三角形的周长小于13，且各边长为互不相等的整数，则这样的三角形共有
做一做：
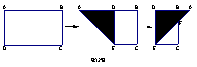
17.用四块如图1的瓷砖拼成一个正方形，使拼成的图案成轴对称图形，请你在图2、图3、图4中各画出一种拼法（要求三种拼法各不相同，所画图案中的阴影部分用斜线表示）.
18. 读一读：式子“1＋2＋3＋4＋5＋……＋100”表示从1开始的100个连续自然数的和.由于上述式子比较长，书写也不方便，为了简便起见，我们可将“1＋2＋3＋4＋5＋……＋100”表示为
，这里“
”是求和符号.例如：“1＋3＋5＋7＋9＋……＋99”（即从1开始的100以内的连续奇数的和）可表示为
；又如“13＋23＋33＋43＋53＋63＋73＋83＋93＋103”可表示为
.同学们，通过对以上材料的阅读，请解答下列问题：
①2＋4＋6＋8＋10＋……＋100（即从2开始的100以内的连续偶数的和）用求和符号可表示为 ；
②计算：
＝
（填写最后的计算结果）
19. 已知：如图，△ABC内接于⊙O1，以AC为直径的⊙O2交BC于点D，AE切⊙O1于点A，交⊙O2于点E.连AD、CE，若AC＝7，AD＝3
，tanB＝
.
求：①BC的长；②CE的长.
 |
20.已知：如图，四边形ABCD为正方形，以AB为直径的半圆O1和以O1C为直径的⊙O2交于点F，连CF并延长交AD于点H，FE⊥AB于点E，BG⊥CH于点G.
①求证：BC＝AE＋BG；②连AF，当正方形ABCD的边长为6时，求四边形ABGF的面积.
21. 如果用□表示1个立方体，用
表示两个立方体叠加，用■表示三个立方体叠加，那么下面左图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（ ）
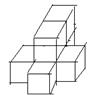
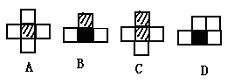
22. 如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（ ）
A．4 B．6 C．8
