中考总复习设计方案型试题
方案决策型题是近年兴起的一种新题型，它的特点是题中给出几种方案让考生通过计算选取最佳方案，或给出设计要求，让考生自己设计方案，这种方案有时不止一种，因而又具有开放型题的特点。此种题型考查考生的数学应用意识强，命题的背景广泛，考生自由施展才华的空间大，因此倍受命题者的青睐。
【命题趋势分析】
例1 我市某地一家农工商公司收获的一种绿色蔬菜，共140吨，若在市场上直接销售，每吨利润为1000元，经粗加工后，每吨利润可达4500元，经精加工后，每吨利润为6500元。该公司加工厂的生产能力是：如果对蔬菜进行粗加工，每天可加工16吨；如果对蔬菜进行精加工，每天可加工6吨；但两种加工方式不能同时进行，受季节等条件限制，公司必须在15天内（含15天）将这批蔬菜全部销售或加工完毕。为此公司研制了两种可行方案：方案一：尽可能多地对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接出售。方案二：将一部分蔬菜进行精加工，其余蔬菜进行粗加工。
（1）写出方案一所获利润W 1；
（2）求出方案二所获利润W 2（元）与精加工蔬菜数
（吨）之间的函数关系式；
（3）你认为怎样安排加工（或直接销售）使公司获利最多？最大利润是多少？
[解答]（1）
＝635000（元）
（2）
＝
（元）
（3）∵15×6＝90
∴自变量的取值范围是：0≤≤90
又∵
随的增大而增大
∴当＝90时，有最大值，最大值为：
＝635000（元）
答：应精加工15天，来不及加工的蔬菜在市场上直接销售，这样安排，公司才能获得最多的利润，最大利润是635000元。
例2 辽南素以“苹果之乡”著称，某乡组织20辆汽车装运三种苹果42吨到外地销售。按规定每辆车只装同一种苹果，且必须装满，每种苹果不少于2车。
（1）设用辆车装运A种苹果，用
辆车装运B种苹果，根据下表提供的信息求与之间的函数关系式，并求的取值范围；
（2）设此次外销活动的利润为W（百元），求W与的函数关系式以及最大利润，并安排相应的车辆分配方案。
| 苹果品种 | A | B | C |
| 每辆汽车运载量 （吨） | 2.2 | 2.1 | 2 |
| 每吨苹果获利 （百元） | 6 | 8 | 5 |
[解答]（1）由题意得：
化简得：
当＝0时，＝10
∴1＜＜10
答：与之间的函数关系式为：；自变量的取值范围是：1＜＜10的整数。
（2）由题意得：W＝
＝
＝
＝
∵W与之间的函数关系式为：＝
∴W随的增大而减小
∴当＝2时，W有最大值，最大值为：
＝315.2（百元）
当＝2时，＝16，
＝2
答：为了获得最大利润，应安排2辆车运输A种苹果，16辆车运输B种苹果，2辆车运输C种苹果。
例3（2003广州）现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为6000元，使用B型车厢每节费用为8000元．
（1）设运送这批货物的总费用为y万元，这列货车挂A型车厢x节，试写出y与x之间的函数关系式；
（2）如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？
（3）在上述方案中，哪个方案运费最省？最少运费为多少元？
[解答]
⑴设用A型车厢x节，则用B型车厢(40－x)节，总运费为y万元 ．
依题意，得 y＝0.6 x＋0.8(40－x)
＝－0.2 x＋32
⑵依题意，得
≥1240，
≥880．
化简，得 10 x≥240， x≥24，
520≥20 x； x≤26．
∴ 24≤x≤26．
∵ x取整数，故A型车厢可用24节或25节或26节．相应有三种装车方案：
①24节A型车厢和16节B型车厢；②25节A型车厢和15节B型车厢；③26节A型车厢和14节B型车厢．
⑶由函数y＝－0.2 x＋32知，x越大，y越少，故当x＝26时，运费最省．
这时 y＝－0.2×26＋32＝26.8(万元)
答：安排A型车厢26节、B型车厢14节运费最省．最小运费为26.8万元．
例4（2002镇江）某企业有员工300人，生产A种产品，平均每人每年可创造利润m万元（m为大于零的常数）。为减员增效，决定从中调配x人去生产新开发的B种产品。根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元。
（1）调配后，企业生产A种产品的年利润为 万元，企业生产B种产品的年利润为 万元（用含x和m的代数式表示）。若设调配后企业全年总利润为y万元，则y关于x的函数解析式为 。
（2）若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的
，生产B种产品的年利润大于调配前企业年利润的一半，应有哪几种调配方案？请设计出来，并指出其中哪种方案全年总利润最大（必要时，运算过程可保留3个有效数字）。
（3）企业决定将“（2）”中的年最大利润（设m=2）继续投资开发新产品，现有6种产品可供选择（不得重复投次同一种产品），各产品所需资金及所获年利润如下表：
| 产 品 | C | D | E | F | G | H |
| 所需资金（万元） | 200 | 348 | 240 | 288 | 240 | 500 |
| 年利润（万元） | 50 | 80 | 20 | 60 | 40 | 85 |
如果你是企业决策者，为使此项投资所获利润不少于145万元，你可以投资开发哪些产品？请写出两种投资方案。
[解答]（1）
，
，
（2）由题意得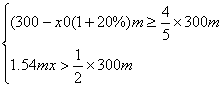
解得
＜≤100。注：写97.5＜≤100或97.4＜≤100均视为正确
∵为整数 ∴只能取98、99、100。
故共有三种调配方案：
①202人继续生产A种产品，调98人生产B种产品；
②201人继续生产A种产品，调99人生产B种产品；
③200人继续生产A种产品，调100人生产B种产品；
又＝
，由于
＞0，函数随的增大而增大。故当＝100，即按第三种方案安排生产时，获总利润最大。
（3）当
＝2时，最大总利润为788万元。根据题意，可投资开发产品F、H或C、D、E或C、D、G或C、F、G。
例5 某工厂现有甲种原料360千克，乙种原料290千克。计划利用这两种材料生产A、B两种产品共50件。已知生产一件A种产品用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元。
（1）按要求安排A、B两种产品的生产件数，有哪几种方案，请你设计出来。
（2）设生产A、B两种产品总利润为y（元），其中一种的生产件数为x，试用含x的代数式表示y，并说明（1）中哪种生产方案获总利润最大，最大总利润是多少？
[解答]（1）设需生产A种产品件，那么需生产B种产品
件，由题意得：
解得：30≤≤32
∵是正整数
∴＝30或31或32
∴有三种生产方案：①生产A种产品30件，生产B种产品20件；②生产A种产品31件，生产B种产品19件；③生产A种产品32件，生产B种产品18件。
（2）由题意得；
＝
∵随的增大而减小
∴当＝30时，有最大值，最大值为：
＝45000（元）
答：与之间的函数关系式为：＝，（1）中方案①获利最大，最大利润为45000元。
例6 某商场设有百货部、服装部和家电部，共有190名售货员，计划全商场日营业额数（指每日卖出商品所收到的总金额）为60万元。由于营业性质不同，分配到三个部的售货员的人数也就不等。根据经验，各类商品每1万元营业额所需售货员人数如表（1），每1万元营业额所得利润情况如表（2）。商场将计划日营业额分配给三个经营部，设分配给百货部、服装部和家电部的营业额分别为（万元）、（万元）、
（万元）（都是整数）。
（1）请用含的代数式分别表示和；
（2）若商场预计每日的总利润为（万元），且1919.7。问这个商场应怎样分配日营业额给三个经营部？各部应分别安排多少名售货员？
表（1）
| 商 品 | 每1万元营业额所需人数 |
| 百 货 类 | 5 |
| 服 装 类 | 4 |
| 家 电 类 | 2 |
表（2）
| 商 品 | 每1万元营业额所得利润 |
| 百 货 类 | 0.3万元 |
| 服 装 类 | 0.5万元 |
| 家 电 类 | 0.2万元 |
[分析]本题文字较长，加之又有两个表格，正确而又全面地读取信息是正确解答本题的前提。
[解答]（1）由题意，得
＋＋=60
5＋4＋2=190
把看成是已知数，解关于、的二元一次方程组，得
=35－
①
=25＋
②
（2）∵
=0.3＋0.5＋0.2
=0.3＋0.5×（35－）＋0.2×（25＋）
=22.5－0.35
∴19≤22.5-0.35≤19.7.
解得8≤≤10.
∵、、是正整数，且由（1）可知应为偶数，
∴=8或10.
当=8时，分别代入①、②得=23，=29
这时分配给三个部门的人数分别为5=40人、4=92人、2=58人。
当=10时，分别代入①、②得=20，=30.
这时分配给三个部门的人数分别为50人、80人、60人。
答：分配给百货部、服装部和家电部的营业额分别为8万元、23万元、29万元，售货员人数分别为40人、92人、58人；或营业额分别为10万元、20万元、30万元，售货员人数分别为50人、80人、60人。
【中考试题精选】
1.2003黄冈已知某电脑公司有A型、B型、C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元．我市东坡中学计划将100 500元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台，请你设计出几种不同的购买方案供该校选择，并说明理由．
2.2002荆州某牛奶加工厂现有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元，制成酸奶销售，每吨可利润率1200元，制成奶片销售，每吨可获取利润2000元，该工厂的生产能力是：如制成酸奶，每天可加工3吨，制成奶片每天可加工1吨，受人员限制，两种加工方式不可同时进行，受气温条件限制，这批牛奶必须在4天内（含第4天）全部销售或加工完毕，为此，该厂设计了两种可行方案：
方案一：尽可能多的制成奶片，其余直接销售鲜牛奶；
方案二：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成。
你认为选择哪种方案获利最多，为什么？
3.2001甘肃某市20位下岗职工在近郊承包50亩土地办农场．这些地可种蔬菜、烟叶或小麦，种这几种农作物每亩地所需职工数和产值预测如下表：
| 作物品种 | 每亩地所需职工数 | 每亩地预计产值 |
| 蔬菜 |
| 1100元 |
| 烟叶 |
| 750元 |
| 小麦 |
| 600元 |
请你设计一个种植方案，使每亩地都种上农作物，20位职工都有工作，且使农作物预计总产值最多．
4.2003资阳已知有12名旅客要从A地赶往40千米外的火车站B乘车外出旅游，列车还有3个小时从B站出站，且他们只有一辆准载4人的小汽车可以利用。设他们的步行速度是每小时4千米，汽车的行驶速度为每小时60千米。
（1）若只用汽车接送，12人都不步行，他们能完全同时乘以这次列车吗？
（2）试设计一种由A地赶往B站的方案，使这些旅客都能同时乘以这次列车。按此方案，这12名旅客全部到达B站时，列车还有多少时间就要出站？（所设计方案若能使全部旅客同时乘上这次列车即可。若能使全部旅客提前20分钟以上同时到达B站，可得2分加分，但全卷总分不得超过100分）
注：用汽车接送旅客时，不计旅客上下车时间。
5.2003泰州某校举行庆祝十六大的文娱汇演，评出一等奖5个，二等奖10个，三等奖15个.学校决定给获奖的学生发奖品，同一等次的奖品相同，并且只能从下表所列物品中选取一件：
| 品 名 | 小提琴 | 运动服 | 笛子 | 舞鞋 | 口琴 | 相册 | 笔记本 | 钢笔 |
| 单价（元） | 120 | 80 | 24 | 22 | 16 | 6 | 5 | 4 |
⑴如果获奖等次越高，奖品单价就越高，那么学校最少要花多少钱买奖品？
⑵学校要求一等奖的奖品单价是二等奖奖品单价的5倍，二等奖的奖品单价是三等奖奖品单价的4倍；在总费用不超过1000元的前提下，有几种购买方案，花费最多的一种方案需要多少钱？
6.2003黄石随着我市教育改革的不断深入，素质教育的全面推进，我市中学生利用假期参加社会实践活动调查的越来越多，张同学在我市J牌公司实习调查时，计划发展部给了他一份实习作业：在下述条件下，规划一个月的产量：假如公司生产部有工人200名，每个工人的月劳动时间不超过192小时，生产一件J牌产品需要一个工人劳动2小时；本月将剩余原料60吨，下个月准备购进出300吨，每件J牌产品需原料20公斤；经市场调查，预计下月市场对J牌产品需求量为16000件，公司准备充分保证市场需求。请你和张同学一起规划下个月的产量范围（设下个月的产量为x件）。
7.2003桂林某公司需在一个月（31天）内完成新建办公楼的装修工程。如果由甲、乙两个工程队合做，12天可完成；如果由甲、乙两队单独做，甲队比乙队少用10天完成。
（1）求甲、乙两工程队单独完成此项工程所需的天数。
（2）如果请甲工程队施工，公司每日需付费用2000元；如果请乙队施工，公司每日需付费用1400元。在规定时间内：A：请甲队单独完成此项工程出。B：请乙队单独完成此项工程；C：请甲、乙两队合作完成此项工程。以上三种方案哪一种花钱最少？
8.2003甘肃某工厂生产某种产品，每件产品的出厂价为1万元，其原材料成本价（含设备损耗等）为0.55万元，同时在生产过程中平均每生产一产品有1吨的废渣产生．为达到国家环保要求，需要对废渣进行脱硫、脱氮等处理，现有两种方案可供选择：
方案一：由工厂对废渣直接进行处理，每处理1吨废渣所用的原料费为0．05万元，并且每月设备维护及损耗费为20万元．
方案二：工厂将废渣集中到废渣处理厂统一处理，每处理1吨废渣需付0．1万元的处理费．
问：
⑴ 设工厂每月生产x件产品，每月利润为y万元，分别求出方案一和方案二处理废渣时，y与x之间的函数关系式（利润＝总收入一总支出）；
⑵ 若你作为工厂负责人，如何根据月生产量选择处理方案，既可达到环保要求又最合算．
9.2003山西启明公司生产某种产品，每件产品的成本是3元，售价是4元，年销售量为10万件。为了获得更好的效益，公司准备拿出一定的资金做广告。根据经验，每年投入的广告费是x（万元），产品的年销售量将是原销售量的y倍，且
，如果把利润看作是销售总额减去成本费和广告费：
（1）写出利润S（万元）与广告费x（万元）的函数关系式。并计算广告是多少万元时，公司获得的利润最大，最大年利润是多少万元？
（2）把（1）中的最大利润留出3万元作广告，现有6个项目可供选择，各项目每股投资金额和预计年收益如下表：
| 项目 | A | B | C | D | E | F |
| 每股（万元） | 5 | 2 | 6 | 4 | 6 | 8 |
| 收益（万元） | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 1 |
如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，问的几种符合要求的投资方式？定出每种投资方式所选的项目。
10.2002四川我市向民族地区的某县赠送一批计算机，首批270台将于近期启程，经与某物流公司联系，得知用A型汽车若干辆刚好装完，用B型汽车不仅可少用一辆，而且有一辆车差30台计算机才装满；
（1）已知B型汽车比A型汽车多装15台，求A、B两种型号的汽车各能装计算机多少台？
（2）已知A型汽车的运费是每辆350元，B型汽车的运费是每辆400元，若运送这批计算机同时用这两种型号的汽车，其中B型汽车比A型汽车多用1辆，所用运费比单独用任何一种型号的汽车都要节省，按这种方案需A、B两种型号的汽车各多少辆？运费多少元？
11.2003黑龙江为了保护环境，某企业决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：
经预算，该企业购买设备的资金不高于105万元．
⑴ 请你设计该企业有几种购买方案；
⑵ 若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
⑶ 在第⑵问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）
12.2002黑龙江为了迎接2002年世界足球赛的到来，某足球协会举办了一次足球联赛，其记分规则及奖励方案如下表：
当比赛进行到第12轮结束（每队均需比赛12场）时，A队共积19分。
（1） 请通过计算，判断A队胜、平、负各几场；
（2）若每赛一场，每名参赛队员均得出场费500元。设A队其中一名参赛队员所得的奖金与出场费的和为W（元），试求W的最大值。
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖金（元/人） | 1500 | 700 | 0 |