初中2006届毕业会考适应性考试
数 学 试 题
| Ⅰ 卷 | Ⅱ 卷 | 总 分 | |||||
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | |
| 得分 | |||||||
第Ⅰ卷(选择题 36分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不能答在本试题卷上.
3.考试结束后,本试卷由考场统一收回,集中管理不上交.
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1.9的相反数是
(A)9 (B)-9 (C) ![]() (D)
(D)![]()
2.下列计算正确的是
 (A)x5+x5=x10 (B)x5·x5=x10 (C)(x5)5=x10 (D)x20÷x2=x10
(A)x5+x5=x10 (B)x5·x5=x10 (C)(x5)5=x10 (D)x20÷x2=x10
3.如图所示,OB⊥OC,∠COD=62°,则∠AOB等于
(A)28° (B)38° (C)14° (D)31°
4.如图,是一个数值转换机,若输入a的值为为-![]() ,
,
![]() 则输出的结果是
则输出的结果是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.在三张同样大小的卡片上分别写上3,5,8三个数,小明从中任意抽取一张作百位,再任意抽取一张作十位,余下的一张作个位,小明抽出的这个数大于500的机会是
 (A)
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
6.如图,点P从B点开始沿BCD匀速运动到D停止,
图形APD的面积为S,运动的时间为t,
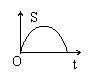
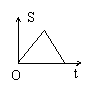
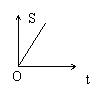
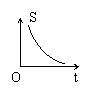 那么s与t的函数图像可能是
那么s与t的函数图像可能是
(A) (B) (C) (D)
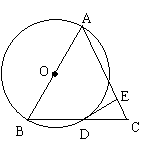
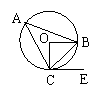 7.如图,△ABC内接于⊙O,EC切⊙O于点C,
7.如图,△ABC内接于⊙O,EC切⊙O于点C,
若∠BOC=76°则∠BCE的度数是
(A)14° (B)38°
 (C)52° (D)76°
(C)52° (D)76°
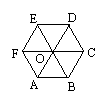
8.如图,O是正六边形ABCDEF的中心,在这个
正六边形中,可以由△AOB平移得到的
三角形的个数是
(A)1 (B)2 (C) 3 (D)4
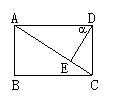 9.如图所示,在矩形ABCD中,DE⊥AC于E,
9.如图所示,在矩形ABCD中,DE⊥AC于E,
设∠ADE=α,且cosα=![]() ,AB=4,则:
,AB=4,则:
AD的长为
(A)3 (B)![]() (C)
(C)![]() (D)
(D)![]()
10.一个由n个相同大小的正方体组成的简单几何体的正视图、俯视图如下:
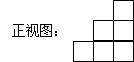
![]()
那么它的左视图不可能是下面的
![]()
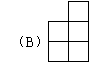
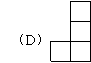
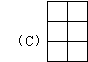
11.小张称P、O、R、S四个砝码在天平上的重量如下图,

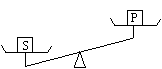
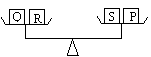
这四个砝码的重量是:可看出这四位小朋友的体重是:
 (A)P<S<Q<R (B)P<S<R<Q (C)P<Q<S<R
(D)Q<P<S<R
(A)P<S<Q<R (B)P<S<R<Q (C)P<Q<S<R
(D)Q<P<S<R
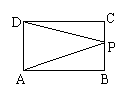
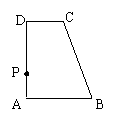
12.如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,
点P是腰AD上的一个动点,要使PC+PB最小,
则应该满足
(A)PB=PC (B)PA=PD
(C)∠BPC=90° (D)∠APB=∠DPC
第Ⅱ卷(非选择题 共114分)
注意事项:1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共6小题,每小题3分,共18分.把答案填在题后的横线上.
 13.函数
13.函数![]() 中,自变量的取值范围是____________.
中,自变量的取值范围是____________.
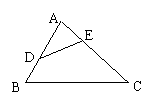
14.如图所示,要使![]() 成立,
成立,
还需添加一个条件(不作辅助线),
你添加的条件是_________________(只填一个条件即可).
15.若![]() ,分解因式mx2-ny2=___________.
,分解因式mx2-ny2=___________.
16.请写出y=-![]() 与y=x2+2的相同点和不同点;
与y=x2+2的相同点和不同点;
相同点:__________________________________;
 不同点:__________________________________.
不同点:__________________________________.
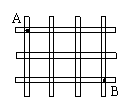
17.一个城市的街道如图所示,A、B表示两个十字路口,
如果用(3,1)→(3,-1)→(4,-1)→(4,-2)
→(5,-2)表示一条从A到B的路线,请用同样的
方式写出另外一条由A到B的路线:
(3,1)→( )→( )→( )→(5,-2).
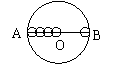
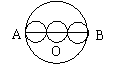
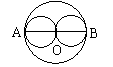
18.如图,AB是⊙O的直径,把线段AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=![]() ,那么⊙O的周长为
,那么⊙O的周长为![]() ,试计算:把AB分成两条相等的线段,每个小圆的周长
,试计算:把AB分成两条相等的线段,每个小圆的周长![]() =______;把AB分成三条相等的线段,每个小圆的周长
=______;把AB分成三条相等的线段,每个小圆的周长![]() =______;……;把AB分成
=______;……;把AB分成![]() 条相等的线段,每个小圆的周长
条相等的线段,每个小圆的周长![]() =
.
=
.
![]()
三、(本大题共3小题,每小题9分,共27分)
19.先化简,再求值:![]() 其中m=
其中m=![]()
20.解方程:![]()
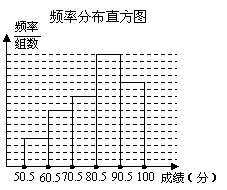
21.一所中学,为了让学生了解环保知识,增强的环保意识,特地举行了一次“保护家乡”的环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分为100分)进行统计.
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100 | ||
| 合计 |
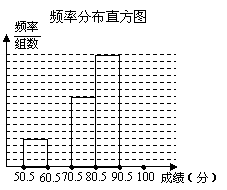 频率分布表
频率分布表
请根据上表和图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中,样本容量是___________;
(4)全体参赛学生中,竞赛成绩的中位数落在哪个组内?
(5)若成绩在90分以上(不含90分)可以获奖,在全校学生的试卷中任抽取一张,获奖的概率是多大?
四、(本大题共3小题,每小题9分,共27分)
22.已知一次函数经过点(1,-1)和(0,3)
(1)求一次函数的解析式;
(2)求函数图象与x轴,y轴所围成的三角形的面积.
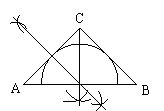
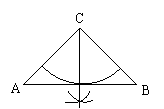
23.在一个铁皮加工厂里有许多形状为同样大小的等腰直角三角形边角铁皮.现找出一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的漏斗,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其它边相切.请设计出三种符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形的半径).
|
甲:如下图,△ABC 中,AB=AC,
以AB为直径作⊙O,与BC
交于点D,过D作AC的垂线,
垂足为E.
 证明:(1)BD=DC;
证明:(1)BD=DC;
(2)DE是⊙O 切线.
注意:你选做的是_____题.
 五、(本大题共2小题,每小题9分,共18分)
五、(本大题共2小题,每小题9分,共18分)
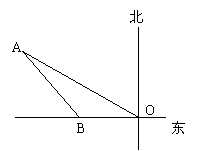
25.如图,在东海中某小岛上有一灯塔A,已知A塔
附近方圆25海里范围内有暗礁.我海军110舰在
O 点处测得A塔在其西北30°方向;再向正西方向
行驶20海里到达B处,测得A塔在其西北方向
45°,如果该舰继续向西航行,是否有触礁的危险?
请通过计算说明理由.
26.等腰梯形ABCD中,AC∥BD,点O在梯形ABCD中,连结AO、BO、CO、DO,
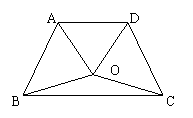 且BO=CO,如图所示,
且BO=CO,如图所示,
(1)求证:AO=DO
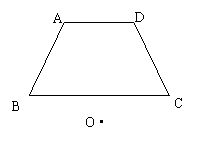 (2)其余条件都不变,只是点O在梯形外,结论还成立吗?
(2)其余条件都不变,只是点O在梯形外,结论还成立吗?
请补充完图形,并说明理由.
六、(本大题共2小题,每小题12分,共24分)
27.某工厂生产的A种产品,它的成本是2元,售价是3元,年销量为100万件,为了获得更好的效益,厂家准备拿出一定的资金做广告;根据统计,每年投入的广告费是x(十万元),产品的年销量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:
| x(十万元) | 0 | 1 | 2 |
| y | 1 | 1.5 | 1.8 |
(1)求y与x的函数关系式;
(2)如果把利润看着销售总额减去成本费和广告费,试写出年利润S(十万元)与广告费x(十万元的函数关系式);
(3)如果投入的年广告费为10万元~30万元,问广告费在什么范围内,工厂获得的利润最大?最大利润是多少?
28.阅读材料:
先看数列:1,2,4,8,…,263.从第二项起,每一项与它的前一项的比都等于2,象这样,一个数列:a1,a2,a3,…,an-1,an ;从它的第二项起,每一项与它的前一项的比都等于一个常数q,那么这个数列就叫等比数列,q叫做等比数列的公比.
根据你的阅读,回答下列问题:
(1)请你写出一个等比数列,并说明公比是多少?
(2)请你判断下列数列是否是等比数列,并说明理由;
![]() ,
,![]() ,
,![]() ,
,![]() ,……;
,……;
(3)有一个等比数列a1,a2,a3,……,an-1,an;已知a1=5,q=-2;请求出它的第25项a25 .
峨眉山市初中2005届毕业会考适应性考试数学试题参考答案
一、ABACA BBBDD DD
二、13.![]() 14.∠AED=∠B等等 15.(x-5y)(x+5y) 16.略 17.略
14.∠AED=∠B等等 15.(x-5y)(x+5y) 16.略 17.略
18.![]()
三、19.解:原式=![]() ,(6分) 当
,(6分) 当![]() 时,原式=
时,原式=![]() (9分)
(9分)
20.解:(x-2)2=0,x=2(7分),经检验x=2是原方程的根(9分)
 21.解:
21.解:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | ||
| 60.5~70.5 | ||
| 70.5~80.5 | ||
| 80.5~90.5 | ||
| 90.5~100 | 12 | 0.24 |
| 合计 | 50 | 1 |
(1)(2)
正确填表2分 正确补全直方图2分
(3)50 (1分) (4)80.5~90.5内(2分) (5)24%(2分)
 四、22.解:(1)y=-4x+3(5分) (2)面积为
四、22.解:(1)y=-4x+3(5分) (2)面积为![]() (4分)
(4分)
 23.
23.
半径为4(3分) 半径为![]() (3分) 半径为2(3分) 半径为4tan22.5°
(3分) 半径为2(3分) 半径为4tan22.5°
任意三种都正确(一种给3分) (半径为或1.66)
24.甲:证明:(1)连结AD,(1分)∵AB是直径,∴AD⊥BC,(3分)又∵AB=AC,∴BD=CD(4分) (2)连结OD,(5分)∵∠BAC=2∠BAD,∠BOD=2∠BAD,
∴∠BAC=∠BOD(6分) ∴OD∥AC(7分),又∵DE⊥AC,∴DE⊥OD(8分)
∴DE是⊙O的切线(9分0
乙:解:(1)△=4m+1 (2分)∵m>0,∴△=4m+1>0(3分)∴方程有两个不相等的实根(4分) (2)x1+x2=![]() ,x1·x2=
,x1·x2=![]() (5分)
(5分)
(x1-5)(x2-5)=x1x2-5(x1+x2)+25=![]() +5×
+5×![]() +25=5m(7分)
+25=5m(7分)
![]() (9分)
(9分)
五、25.解:不会触礁(2分);过A作AC⊥BO,垂足为C(3分),设AC=x,
∵∠ABC=45°,∴BC=x,(4分)![]() ,
,![]() (8分),所以没有触礁的危险(9分)
(8分),所以没有触礁的危险(9分)
26.(1)证明:∵在等腰梯形ABCD中,AB=DC,∴∠ABC=∠DCB(1分),又∵BO=CO,∴∠OBC=∠OCB(2分)∴∠ABO=∠DCO(3分)∴△ABO≌△DCO(4分)
∴AO=OD(5分) (2)成立(6分)补充完图形(7分)理由说明正确(9分)
六、27.解:(1)y=0.1x2+0.6x+1(4分)
(2)S=3×100y-2×100y-x=-10x2+59x+100 (4分)
(3)x=2.95时利润最大,最大利润为187.025(十万元) 答略(4分)
28.(1)等比数列、公比都正确 (4分)
(2)不是(5分)因为![]() 而
而![]() ,所以不是等比数列(8分)
,所以不是等比数列(8分)
(3)a25=5×224 (12分)