初高中衔接型数学中考试题（1）及参考答案
一、选择题
1、（2003荆门）64名男子乒乓球选手进行单打淘汰赛（胜者进入下一轮，败者淘汰出局），直至决出单打冠军，共比赛的场次是（ ）
A、32场 B、62场 C、63场 D、64场
2、（2003黑龙江）从哈尔滨开往A市的特快列车，途中要停靠两个站点，如果任意两站间的票价都不同，那么有（ ）种不同的票价．
（A）4 （B）6
（C）10 （D） 12
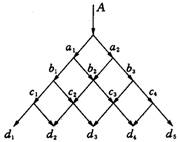
3、（2003南宁）一条信息可通过如图7的网络线由上（A点）往下向各站点传送．例如信息到b2点可由经a1的站点送达，也可由经a2的站点送达，共有两条途径传送．则信息由A点到达d3的不同途径共有（ ）．
（A）3条（B）4条（C）6条（D）12条
二、填空题
1、（2003河北）乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要安排不同的车票 种。
2、（2003山西）联欢会上，小红按照4个红气球、3个黄气球、2个绿气球的顺序把气球串起来装饰会场，第52个气球的颜色是 。
3、（2002桂林）观察下列分母有理化的计算：
，
，
，
，…从计算结果中找出规律，并利用这一规律计算：
=
．
=
．
4、（2002十堰）有A1、A2、A3三个舞蹈演员在舞台上跳舞，面对观众作队形排列变化，其变化规律是：
一个舞蹈演员A1跳舞，面对观众作队形排列变化的种数是A1为1种；
二个舞蹈演员A1、A2跳舞，面对观众作队形排列变化的种数是A1A2 ；A2A1为2种即1×2种；
三个舞蹈演员A1、A2、A3跳舞，面对观众作队形排列变化的种数是A1A2A3 ，A1 A3A2 ；A2A1A3 ，A2 A3 A1；A3A1A2 ，A3 A2A1为6种即1×2×3种；
请你推测：
（1） 四个舞蹈演员A1、A2、A3、A4跳舞，面对观众作队形排列变化的种数是_______种；
（2） 六个舞蹈演员跳舞，按照上述方法作队形排列变化的种数为（用科学记数法表示）__________种；
（3） 用1、2、3、4、5、6、7共7个数字排列成7位数的电话号码（在同一个电话号码内每个数字只能用一次）可排成_________个电话号码。
5、小明是一位刻苦学习、勤于思考、勇于创造的同学。一天，他在解方程时，突然产生了这样的想法，x2=-1这个方程在实数范围内无解，如果存在一个数i2=-1,那么方程x2=-1可以变为x2=i2,则x=+i,从而x=+i是方程x2=-1的两个根。小明还发现i具有如下性质：
i1=i;i2=-1;i3=i2×i=(-1)×i=-i;i4=(i2)2=(-1)2=1;i5=i4×i=i;i6=(i2)3=(-1)3=-1;i7=i6×i=-i;i8=(i4)2=1……,请你观察上述各式，根据你发现的规律填空：i4n+1=
,i4n+2=
，i4n+3=
(n为自然数)。
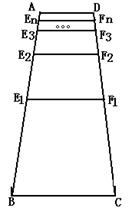
6、如图，梯形ABCD中上底AD＝a，下底BC＝b，
若E1F1分别为AB，CD的中点，则E1F1＝
；
若E2F2分别为AE1、DF1的中点，则E2F2＝
；
若E3F3分别为AE2、DF2的中点，则E3F3＝
……；若E6F6分别为AE5、DF5的中点，则E6F6＝＿＿＿＿
试题 参考答案
一1、答：C。分析：运用逆向思维，从“每淘汰一名选手出局必须进行一场比赛”的事实出发，直到决出单打冠军，必须淘汰63名选手，所以一共要进行63场比赛。
评点：逆向思维是学习知识、解决问题的一种重要思维方法，在数学知识中有很多运用逆向思维得到的知识：比如由整式乘法逆向思维可得到因式分解的方法；由互逆命题经过证明可以得到互逆定理：很多几何图形的判定和性质就是这样的。
2、答：B。分析：可转化为一条直线上四个点能组成多少条线段的问题。
评点：转化的思想是一种重要的数学思想方法，建立适当的数学模型是解决问题的关键。
引申：一条直线上五个点能组成多少条线段？n个点呢？
3、答：C。分析：本题可应用“穷举法”解决。
二、1、答：10。分析：4+3+2+1=10。
2、答：黄色。分析：52=9×5+7，第45个气球是绿的，再数7个，应是黄气球。
评点：学会探索，发现规律，是解决本题的关键。
3、答：2001，2002。
解：
=
=
=2002－１=2001
评：“裂项相消法”是高中代数数列求和的重要方法之一，又如
可用于化简
，等等。
4、答：（1）24种； （2）
。
解：（1）
；（2）
评：从简单到复杂、从具体到抽象是我们认识客观世界的重要手段，也是我们思考解决数学问题的重要解题策略，本题知识点和方法正是高中代数将要学习的排列与组合内容。
5、答：
，－1，
解：
，
评：“大胆地想象，仔细地论证”是我们求知者应具备的素质，创新与发现就这样产生。
本题是在初二对有理数突破到实数产生无理数以后，又一次大胆的突破，是高中代数复数、虚数概念的一处伏笔。
6、答：
。解：
评：多实践，多试探，找规律。