2005年中考复习数学综合测试题(1)
一.填空题:(每小题3分,共30分)
1.-7的绝对值是 ,![]() 的倒数是 .
的倒数是 .
2.分解因式:![]() =
.
=
.
3.已知![]() 是完全平方式,则
是完全平方式,则![]() .
.
4.反比例函数![]() 的图象与坐标轴有 个交点,图象在
象限,当
的图象与坐标轴有 个交点,图象在
象限,当![]() >0时函数值
>0时函数值![]() 随
随![]() 的增大而
.
的增大而
.
5.某果园有果树200棵,从中随机抽取5棵,每棵果树的产量如下:(单位:千克)
98 102 97 103 105.这5棵果树的平均产量为 千克,估计这200棵果树的总产量约为 千克.
 6.把抛物线
6.把抛物线![]() 向上平移2个单位,那么所得抛物线与x轴
向上平移2个单位,那么所得抛物线与x轴
的两个交点之间的距离是 .
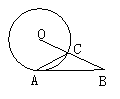
7.如图,沿倾斜角为30º的山坡植树,要求相邻两棵树间的水平
距离AC为![]() ,那么相邻两棵树的斜坡距离AB约为_________
,那么相邻两棵树的斜坡距离AB约为_________![]() ;
;
 (结果精确到0.1m,可能用到的数据:).
(结果精确到0.1m,可能用到的数据:).
8.用两块完全重合的等腰三角形纸片能拼出下列图形
.
9.如图:⊙O与AB相切于点A,BO与⊙O交于点C,
![]() ,则
,则![]() 等于
.
等于
.
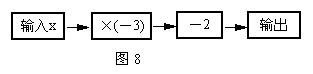 10.如图,是一个简单的数值运算程序当输入
10.如图,是一个简单的数值运算程序当输入![]() 的值为-1时,则输出的数值为 .
的值为-1时,则输出的数值为 .
二.选择题:(每小题4分,共24分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的。
11.世界文化遗产长城总长约6 700 000![]() ,用科学记数法可表示为( )
,用科学记数法可表示为( )
(A)
6.7×105![]() (B) 6.7×
(B) 6.7×![]()
![]() (C) 6.7×106
(C) 6.7×106![]() (D) 6.7×
(D) 6.7×![]()
![]()
12.将一圆形纸片对折后再对折,得到图2,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )


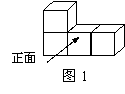
13.图1中几何体的主视图是( )
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
14.在选取样本时,下列说法不正确的是( )
(A)所选样本必须足够大 (B)所选样本要具有普遍代表性
![]() (C)所选样本可按自己的爱好抽取;(D)仅仅增加调查人数不一定能提高调查质量
(C)所选样本可按自己的爱好抽取;(D)仅仅增加调查人数不一定能提高调查质量
15.将图形按顺时针方向旋转900后的图形是( )
(A) (B) (C) (D)
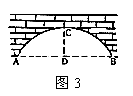 16.如图3,圆弧形桥拱的跨度AB=12米,拱高CD=4米,
16.如图3,圆弧形桥拱的跨度AB=12米,拱高CD=4米,
则拱桥的半径为
(A)6.5米 (B)9米 (C)3米 (D)15米
三.解答题:(96分)
17.(7分)计算:![]() .
.
18.(10分)先化简,在求值:![]() ,其中
,其中![]() .
.
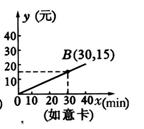
19.(8分)为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在玉溪市范围内每月(30天)的通话时间![]() (min)与通话费y(元)的关系如图所示:
(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费![]() 、
、![]() 与通话时间
与通话时间![]() 之间的函数关系式;
之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜?
 | |||
 | |||
20.(10分)等腰梯形一底的中点对边的两个端点的距离会相等吗?若相等,请给出证明。若不相等,请说明理由。
21.(12分)如图8,PA切⊙O于点A,PBC交⊙O于点B、C,若PB、PC的长是关于x的方程![]() 的两根,且BC=4,求:(1)m的值;(2)PA的长;
的两根,且BC=4,求:(1)m的值;(2)PA的长;

22.(9分).有两个布袋,甲布袋有12只白球,8只黑球,10只红球;乙布袋中有3只白球,2只黄球,所有小球除颜色外都相同,且各袋中小球均已搅匀。
(1)如果任意摸出1球,你想摸到白球,你认为选择哪个布袋成功的机会较大?
(2)如果又有一布袋丙中有32只白球,14只黑球,4只黄球,你又选择哪个布袋呢?
23.(10分)已知双曲线![]() 和直线
和直线![]() 相交于点A(
相交于点A(![]() ,
,![]() )和点B(
)和点B(![]() ,
,![]() ),且
),且![]() ,求
,求![]() 的值.
的值.
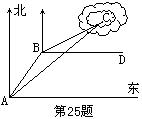
24.(10分)一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
25. (10分)如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
 |
26.
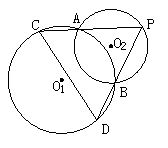
(10分)已知:如图,⊙O![]() 和⊙O
和⊙O![]() 相交于A、B两点, 动点P在⊙O
相交于A、B两点, 动点P在⊙O![]() 上,且在⊙
上,且在⊙![]() 外,直线PA、PB分别交⊙O
外,直线PA、PB分别交⊙O![]() 于C、D.问:⊙O
于C、D.问:⊙O![]() 的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
答案
一.填空题:(每小题3分,共30分)
1.![]() ,
,![]() ;
;
2.![]() ;
;
3.![]() ;
;
4.0个,一、三,减小;
5.101,20200;
6.![]() ;
;
7.约为![]() ;
;
8.平行四边形,正方形,等腰直角三角形;
9.![]() ;
;
10.1;
二.选择题(每小题4分,共24分)
11.C;
12.C;
13.D;
14.C;
15.D;
16.A;
三.解答题:(96分)
17.原式![]()
18.原式![]()
当![]() 时;
时;
原式![]()
19.解: (1)![]()
![]()
(2)当![]() 时,
时,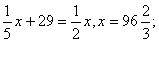
当![]() 时,
时,![]()
所以,当通话时间等于96![]() min时,两种卡的收费一致;当通话时间小于
min时,两种卡的收费一致;当通话时间小于![]() mim时,“如意卡便宜”;当通话时间大于
mim时,“如意卡便宜”;当通话时间大于![]() min时,“便民卡”便宜。
min时,“便民卡”便宜。
20.会相等,画出图形,
写出已知、求证;
 无论中点在上底或下底,
无论中点在上底或下底,
均可利用等腰梯形同一
底上的两底角相等和腰
相等加上中点定义,运
用“SAS”完成证明。
21.
解:由题意知:(1)PB+PC=8,BC=PC-PB=2
 ∴PB=2,PC=6
∴PB=2,PC=6
∴PB·PC=(m+2)=12
∴m=10
(2)∴PA2=PB·PC=12
∴PA=![]()
22.运用概率知识说明:(1)乙布袋,(2)丙布袋.
23.解:由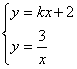 ,得
,得![]()
∴![]() =-
=-![]() ,
,![]() =-
=-![]()
故![]() =(
=(![]() )2-2
)2-2![]() =
=![]() =10
=10
∴![]() ∴
∴![]() 或
或![]() ,
,
又△![]() 即
即![]() ,舍去
,舍去![]() ,故所求
,故所求![]() 值为1.
值为1.
24.解法一:过点B作BM⊥AH于M,∴BM∥AF.∴∠ABM=∠BAF=30°.
在△BAM中,AM=![]() AB=5,BM=
AB=5,BM=![]() .
.
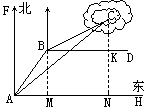 过点C作CN⊥AH于N,交BD于K.
过点C作CN⊥AH于N,交BD于K.
在Rt△BCK中,∠CBK=90°-60°=30°
设CK=![]() ,则BK=
,则BK=![]()
在Rt△ACN中,∵∠CAN=90°-45°=45°,
∴AN=NC.∴AM+MN=CK+KN.
又NM=BK,BM=KN.
∴![]() .解得
.解得![]()
∵5海里>4.8海里,∴渔船没有进入养殖场的危险.
答:这艘渔船没有进入养殖场危险.
解法二:过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.
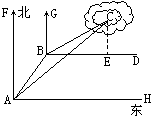 ∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.
∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.
∴∠BCA=∠BCE-∠ACE=60°-45°=15°.
又∠BAC=∠FAC-∠FAB=45°-30°=15°,
∴∠BCA=∠BAC.∴BC=AB=10.
在Rt△BCE中,CE=BC·cos∠BCE=BC·cos60°=10×![]() =5(海里).
=5(海里).
∵5海里>4.8海里,∴渔船没有进入养殖场的危险.
答:这艘渔船没有进入养殖场的危险.
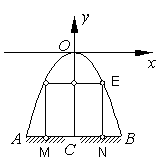 25.解:(1)设所求函数的解析式为
25.解:(1)设所求函数的解析式为![]() .
.
由题意,得 函数图象经过点B(3,-5),
∴-5=9a.
∴![]() .
.
∴所求的二次函数的解析式为![]() .
.
x的取值范围是![]() .
.
(2)当车宽![]() 米时,此时CN为
米时,此时CN为![]() 米,对应
米,对应![]() ,
,
EN长为![]() ,车高
,车高![]() 米,∵
米,∵![]() ,
,
∴农用货车能够通过此隧道。
26.解:当点P运动时,CD的长保持不变,A、B是⊙O![]() 与⊙O
与⊙O![]() 的交点,弦AB与点P的位置关系无关,连结AD,∠ADP在⊙O
的交点,弦AB与点P的位置关系无关,连结AD,∠ADP在⊙O![]() 中所对的弦为AB,所以∠ADP为定值,∠P在⊙O
中所对的弦为AB,所以∠ADP为定值,∠P在⊙O![]() 中所对的弦为AB,所以∠P为定值.
中所对的弦为AB,所以∠P为定值.
∵∠CAD =∠ADP +∠P,
∴∠CAD为定值,
在⊙O![]() 中∠CAD对弦CD,
中∠CAD对弦CD,
∴CD的长与点P的位置无关.毛