中考试题精选（一）
一、选择填空题
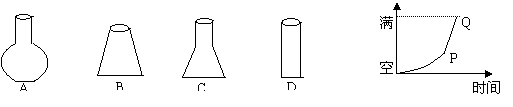1、向一容器内均匀注水，最后把容器注满.在注水过程中，容器的水面高度与时间的关系如右图所示，图中PQ为一线段，则这个容器是-------------------------（ ）
2、下图是正方体分割后的一部分，它的另一部分为下列图形中的--------------------（ ）
 |
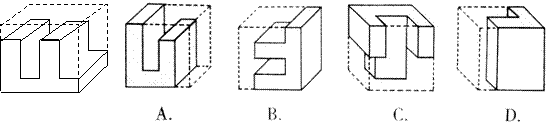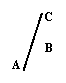
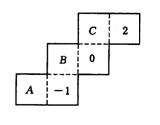3、如图是一个正方体包装盒的表面展开图，若在其中的三个正方形A、B、C内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在A、B、C内的三个数依次是----------------------------（ ）
（A）0，－2，1 （B）0，1，－2（C）1，0，－2（D）－2，0，1
4、图(1)是一个水平摆放的小正方体木块，图(2)、(3)是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是---------------------------( )
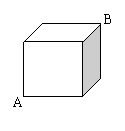
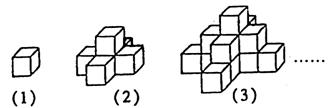
(A)25 (B)66 (C)91 (D)120
5、如图，一只蚂蚁沿边长为
的正方体表面从顶点A爬到顶点B，则
它走过的路程最短为---------------------------------（ ）
A、
B、
C、
D、
6、下列图中阴影部分的面积与算式
的结果相同的是----------------（ ）
7、如图，为做一个试管架，在acm长的木条上钻了4个圆孔，每个孔的直径为2cm，则x等于---------------------------------------------------------------------------------------------（ ）
|
B．
C．
D．
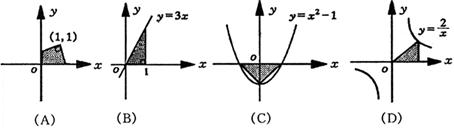
8、如图，四个半径均为R的等圆彼此相切，则图中阴影部分（形似水壶）图形的面积为
A、
； B、
； C、
； D、
9、如图：矩形花园ABCD中，
，
，花园中建有一条矩形道路LMPQ及一条平行四边形道路RSTK。若
，则花园中可绿化部分的面积为----（ ）
（A）
（B）
（C）
（D）
10、
某兴趣小组做实验，将一个装满水的啤酒瓶倒置（如图（5）），并设法使瓶里的水从
瓶中匀速流出。那么该倒置啤酒瓶内水面高度h随水流出的时间t变化的图象大致（ ）
11如图，在方格纸中有四个图形<1>、<2>、<3>、<4>，其中面积相等的图形是（ ）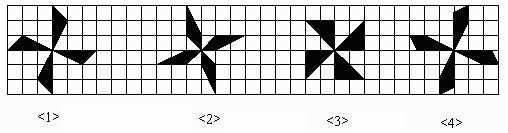
A. <1>和<2> B. <2>和<3> C. <2>和<4> D. <1>和<4>
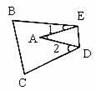12、如图，把
纸片沿DE折叠，当点A落在四边形BCDE内部时，则
与
之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）
A. 
B.
C. 
D. 
|
A．
B．
C．
D．
14、如图是某蓄水池的横断面示意图，分深水区和浅水区，如果这个蓄水池以固定的流量注水，下面哪个图象能大致表示水的最大深度h和时间t之间的关系？-------（ ）．
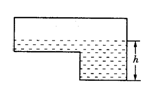
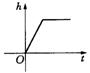
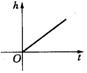
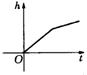
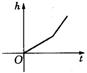
（A） （B）
（C） （D）
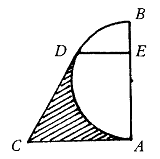
15、如图，等腰梯形ABCD的上底BC长为1，弧OB、弧OD、弧BD的半径相等，弧OB、弧BD所在圆的圆心分别为A、O．则图中阴影部分的面积是---------------（ ）
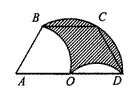（A）
（B）
（C）
（D）
16、某人骑车外出，所行的路程S（千米）与时间t（小时）的函数关系如图所示，现有下列四种说法：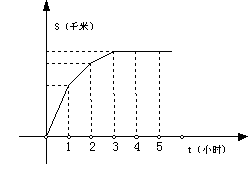
① 第3小时中的速度比第1小时中的速度快；②第3小时中的速度比第1小时中的速度慢；③第3小时后已停止前进；
④第3小时后保持匀速前进。
其中说法正确的是-------------------------（ ）
（A）②、③ （B）①、③
（C）①、④ （D）②、④
17、如图：请根据小文在镜中的像写出他的运动衣上的实际号码： 。
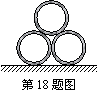
18、如图，施工工地的水平地面上，有三根外径都是1米的水泥管，两两相切地堆放在一起，则其最高点到地面的距离是 ．
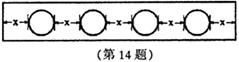
19、如图，某燃料公司的院内堆放着10个外径为1米的空油桶，为了防雨需搭建简易防
雨蓬，这个防雨棚的高度最低应为___________
|
 |
20、某种树木的分枝生长规律如图所示，则预计到第6年时，树木的分
枝数为
.
21、一个正方体的每个面分别标有数字1、2、3、4、5、6。根据图1中该正方体A、B、C三种状态所显示的数字，可推出“？”处的数字是 。
22、如图，五边形ABCDE是正五边形，曲线EFGHIJ……叫做“正五边形 ABCDE的渐开线”，其中EF、FG、GH、HI、IJ…的圆心依次按A、B、C、D、E循环，它们依次相连接。如果AB＝1，那么曲线 EFGHIJ的长度为
（结果保留
）
23、光线以图所示的角度α照射到平面镜Ⅰ上，然后在平面镜Ⅰ、Ⅱ之间来回反射，已知∠α=60°，∠β=50°，∠γ=
度。
24、如图，已知矩形ABCD中，AD=2AB=2，以B为圆心，以BA为半径作圆弧交CB的延长线于E，则图中阴影部分的面积是 .
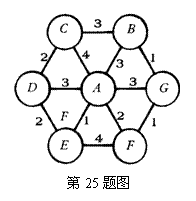
25、某综合性大学拟建校园局域网络，将大学本部A和所属专业学院 B、C、D、E、F、G之间用网线连接起来．经过测算，网线费用如图如示（单位：万元），每个数字表示对应网线（线段）的费用．实际建同时，部分网线可以省略不建，但本部及所属专业学院之间可以传递信息，那么建网所需的最少网线费用为 万元。
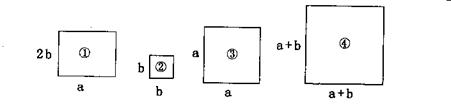
26、下列四个图形中，图①是长方形，图②、③、④是正方形。
把图①、②、③三个图形拼在一起（不重合），其面积为S，
则S=_______；图④的面积P=______；则P_______S.
27、下面是按照一定规律画出的一列“树型”图：
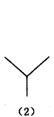
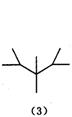
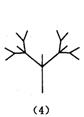
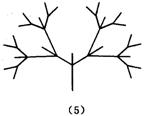
经观察可以发现：图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，图（7）比图（6）多出
个“树枝”．
28、阅读下列一段话，并解决后面的问题 .
观察下面一例数：
1，2，4，8，……
我们发现，这一列数从第2项起，每一项与它前一项的比都等于2 .
一般地，如果一列数从第2项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比数列，这个常数叫做等比数列的公比 .
（1）等比数列5，－15，45，……的第4项是 ；
（2）如果一列数
，
，
，
，……是等比数列，且公比为q，那么根据上述的规定，有
，
，
，……
所以
，
，
，
……
.（用与q的代数式表示）
（3）一个等比数列的第2项是10，第3项是20，求它的第1项与第4项
29、读一读：式子“1＋2＋3＋4＋5＋……＋100”表示从1开始的100个连续自然数的和.由于上述式子比较长，书写也不方便，为了简便起见，我们可将“1＋2＋3＋4＋5＋……＋100”表示为
，这里“
”是求和符号.例如：“1＋3＋5＋7＋9＋……＋99”（即从1开始的100以内的连续奇数的和）可表示为
；又如“13＋23＋33＋43＋53＋63＋73＋83＋93＋103”可表示为
.同学们，通过对以上材料的阅读，请解答下列问题：
①2＋4＋6＋8＋10＋……＋100（即从2开始的100以内的连续偶数的和）用求和符号可表示为 ；
②计算：
＝
（填写最后的计算结果）
30、下面四个图形中，从几何图形的性质考虑，哪一个与其它三个不同？请指出这个图形，并简述你的理由．
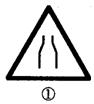
答：图形 ；理由是
：
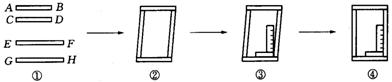
31、工人师傅做铝合金窗框分下面三个步骤进行：
⑴ 先截出两对符合规格的铝合金窗料（如图①），使AB＝CD，EF＝GH；
⑵ 摆放成如图②的四边形，则这时窗框的形状是
形，根据的数学道理是：
；
⑶ 将直角尺靠紧窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是
形，根据的数学道理是：
；
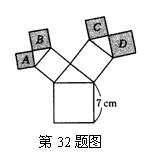
32、如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A、B、C、D的面积的和是
．
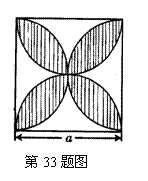33、如图，正方形的边长为a，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为
|
| ||||
34、如图，由边长为1的25个小正方形组成的正方形网格上有一个△ABC；在网格上画出一个与△ABC相似且面积最大的△A1B1C1，使它的三个顶点都落在小正方形的顶点上，则△A1B1C1的最大面积是__________.
二、非填选题
35、下面是同学们玩过的“锤子、剪子、布”的游戏规则：游戏在两位同学之间进行,用伸出拳头表示“锤子”，伸出食指和中指表示“剪子”，伸出手掌表示“布”，两人同时口念“锤子、剪子、布”，一念到“布”时，同时出手，“布”赢“锤子”，“锤子”赢“剪子”，“剪子”赢“布”。
现在我们约定：“布”赢“锤子”得9分，“锤子”赢“剪子”得5分，“剪子”赢“布”得2分。
(1)小明和某同学玩此游戏过程中，小明赢了21次，得108分，其中“剪子”赢“布”7次。聪明的同学，请你用所学的数学知识求出小明“布”赢“锤子”、“锤子”赢“剪子”各多少次？
（2）如果小明与某同学玩了若干次，得了30分，请你探究一下小明各种可能的赢法，并选择其中的三种赢法填入下表。
赢法一：
| “布”赢“锤子” | “锤子”赢“剪子” | “剪子”赢“布” | |
| 赢的次数 |
赢法二：
| “布”赢“锤子” | “锤子”赢“剪子” | “剪子”赢“布” | |
| 赢的次数 |
赢法三：
| “布”赢“锤子” | “锤子”赢“剪子” | “剪子”赢“布” | |
| 赢的次数 |
36、如图，正三角形ABC的边长为1cm，将线段AC绕点A顺时针旋转120°至AP1，形成扇形D1；将线段BP1绕点B顺时针旋转120°至BP2，形成扇形D2；将线段CP2绕点C顺时针旋转120°至CP3，形成扇形D3；将线段AP3绕点A顺时针旋转120°至AP4，形成扇形D4……。设
为扇形Dn的弧长（n=1，2，3……）,回答下列问题：
（1）按照要求填表：
| n | 1 | 2 | 3 | 4 |
|
|
（2）根据上表所反映的规律，试估计n至少为何值时，扇形Dn的湖长能绕地球赤道一周？（设地球赤道半径为6400km）。
37、如图：有两个正方形的花坛，准备把每个花坛都分成形状相同的四块，种不同的花草，下面左边的两个图案是设计示例，请你在右边的两个正方形中再设计两个不同的图案。
38、如图，在△ABC中，∠C=90°，AC=6，BC=8，M是BC的中点，P为AB上的一个动点，（可以与A、B重合），并作∠MPD=90°，PD交BC（或BC的延长线）于点D.
（1）记BP的长为x，△BPM的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
（2）是否存在这样的点P，使得△MPD与△ABC相似？若存在，请求出x的值；若不存在，请说明理由.
38．（1）作PK⊥BC于K，BM＝4，AB＝10，
∵PK∥AC，∴
=
pk＝
x，
∴y＝
×4×x＝
x（0<x<10）.
（2）①∠PMB=∠B,
PM=PB ,MK=KB=2 , =
， x=2.5；
②∠PMD=∠A,
又∠B =∠B，∴△BPM∽△BAC，
∴BP·AB＝BM·BC，
∴10x=4×8 ，x＝3.2，
∴存在 x＝2.5或3.2.