2006年中考全真模拟试卷(七)
(满分150分 时间120分钟)
一、选择题(每题3分,共36分.每小题有四个选项,其中只有一个选项是正确的,将正确选项的字母填入下表相应的题号下面.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、已知实数![]() 在数轴上对应的点如图所示,则下列式子正确的是( ).
在数轴上对应的点如图所示,则下列式子正确的是( ).
 A.
A.![]()
![]() B.
B.![]()
C.![]() D.
D.![]()
2、下列根式与是同类根式的是( )
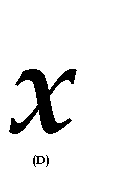 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.下列图形中,轴对称图形是( )



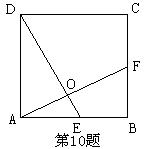
4、 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、 F,那么阴影部分的面积是矩形ABCD面积的 ( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、已知⊙![]() 和⊙
和⊙![]() 的半径分别为2cm和3cm,两圆的圆心距是 5cm,则两圆的位置关系是(
)
的半径分别为2cm和3cm,两圆的圆心距是 5cm,则两圆的位置关系是(
)
A、相交 B、外离 C、内切 D、外切
6、函数![]() 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、使用同一种规格的下列地砖,不能密铺的是( )
A、正六边形地砖 B、正五边形地砖
C、正方形地砖 D、正三角形地砖
8、如图,希望中学制作了学生选择棋类、武术、摄影、
刺绣四门校本课程情况的扇形统计图. 从图中可以看
出选择刺绣的学生为( ).
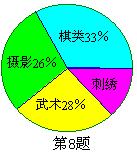 (A)11% (B)12% (C) 13% (D) 14%
(A)11% (B)12% (C) 13% (D) 14%
9、 中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,
![]() 与
与![]() 相交于点
相交于点![]() ,则
,则![]() (
).
(
). 
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、 抛物线![]() 的图像与x轴交于(x1,0)(x2,0)两点,且0< x1<1,1<
x2<2,且与y轴交于点(0,-2)。下列结论: (1)2a+b>1
(2)3a+b>0 (3)a+b<2 (4)a<-1.其中正确的结论的个数为(
)个。
的图像与x轴交于(x1,0)(x2,0)两点,且0< x1<1,1<
x2<2,且与y轴交于点(0,-2)。下列结论: (1)2a+b>1
(2)3a+b>0 (3)a+b<2 (4)a<-1.其中正确的结论的个数为(
)个。
A、1 B、2 C、3 D、4
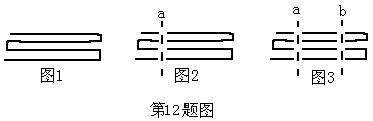
12、一根绳子弯曲成如图1所示的形状发,当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(a∥b)把绳子再剪一次时,绳子就被剪为9段;。若用剪刀在虚线a、b之间把绳子再剪(n-2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是( )
A、4n+1 B、4n+2 C、4n+3 D、4n+5
二、填空题:(每小题4分,共24分,请把答案填在其中的横线上.)
13、最简根式![]() 是同类二次根式,
是同类二次根式,![]() ___________.
___________.
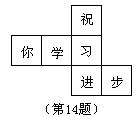
14、水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。如图是一个正方体的平面展开图,若图中的“进”表示正方体的前面,“步” 表示右面,“习”表示下面,则“祝”“你”“学”分别表示正方体的 .
15、民意商场对某种商品作调价,按原价8折出售,此时商品的利润是10%,此商品的进价为1000元,则商品的原价是____________.
 16、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______.
16、如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______.
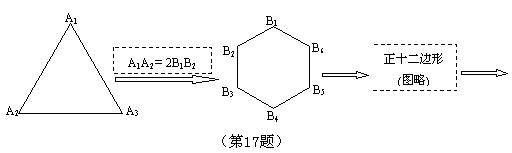
17、 如图,一个正三角形经过变换依次成为正六边形、正十二边形、正二十四边形、….当这些正多边形的周长都相等时,正六边形的面积 正十二边形的面积(填不等的符号).
18、⊙O的半径OA=2,弦AB、AC的长分别为一元二次方程![]() 的两个根,则∠BAC的度数为 。
的两个根,则∠BAC的度数为 。
三、解答题 (本大题共8题,计90分.解答时应写明演算步骤、证明过程或必要的文字说明.)
19、(本题满分8分)
先化简再求值.![]() ,其中
,其中![]() .
.
20、(本题满分10分)
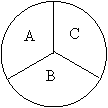
如图,盒中装有完全相同的球,分别标有“A”, “B” ,“C”,从盒中随意摸出一球,并自由转动转盘(转盘被分成三个面积相等的扇形),小刚和小明用它们做游戏,并约定:如果所摸出的球上字母与转盘停止后指针对准的字母相同,则小明获得1分,如果不同,则小刚获得1分。
(1)你认为这个游戏公平吗?为什么?
(2)如果不公平,该如何修改约定,才能使游戏对双方公平?
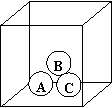 |  |
21. (本题满分10分)
在下面的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移5格后的△A1B1C1,再画出△ABC以点O为旋转中心,沿顺时针方向旋转90°后的△A2B2C2;
(2)如图,以点O为原点建立平面直角坐标系,试写出点A2、B1的坐标.

|
![]()
22、(本题满分12分)
某商场进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会,(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
| 奖次 | 特等奖 | 一等奖 | 二等奖 |
|
| 圆心角 | 1° | 10° | 30° | 90° |
(1)获得圆珠笔的概率是多少?
(2)如果不用转盘,请设计一种等效实验方案.
(要求写清楚替代工具和实验规则)
23、(本题满分12分)
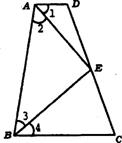
如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
(1)用序号写出一个真命题(书写形式如:如果×××,那么××),并给出证明:
(2)用序号再写出三个真命题(不要求证明);
(3)加分题:真命题不止以上四个,想一想,就能够多写出几个真命题,每多写出一个真命题就给你加1分,最多加2分.
24、(本题满分12 分)
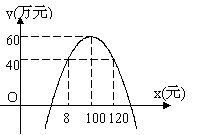
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
⑴求y关于x的函数关系式;
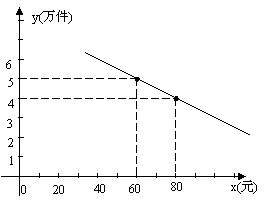 ⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑶若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
![]()
25、(本题满分12分)
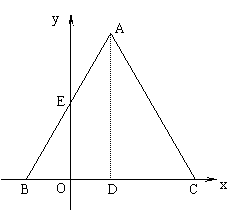
已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)
(1) 求点A、E的坐标;
(2) 若y=![]() 过点A、E,求抛物线的解析式。
过点A、E,求抛物线的解析式。
(3) 连结PB、PD,设L为△PBD的周长,当L取最小值时,求点P的坐标及L的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由。
 |
![]()
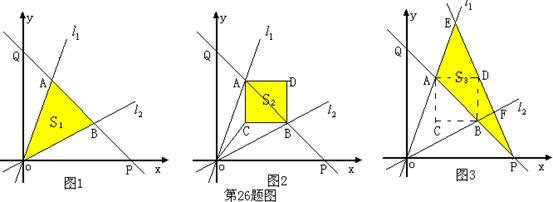
26、(本题满分14分)如图:过原点的直线 ![]() 点P从原点出发沿x轴正方向以每秒1个单位长度的速度运动。直线PQ交于y轴正半轴于点Q,且分别交
点P从原点出发沿x轴正方向以每秒1个单位长度的速度运动。直线PQ交于y轴正半轴于点Q,且分别交 ![]() 于点A、B。设点P的运动时间为t秒时,直线PQ的解析式为
于点A、B。设点P的运动时间为t秒时,直线PQ的解析式为![]() 。△AOB的面积为S1(如图1),以AB为对角线作正方形ABCD,其面积为S2(如图2)。连接PD并延长,交
。△AOB的面积为S1(如图1),以AB为对角线作正方形ABCD,其面积为S2(如图2)。连接PD并延长,交![]() 于点E,交
于点E,交![]() 于点F。设△PEA的面积为S3(如图3)。
于点F。设△PEA的面积为S3(如图3)。
(1)求S1关于t的函数解析式;(2)求直线OC的函数解析式;
(3)求S2关于t的函数解析式;(4)求S3关于t的函数解析式。
2006年中考全真模拟试卷(七)参考答案
一、选择题 :
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | B | B | D | D | B | C | B | A | A | A |
二、填空题:
13、1 ;
14、后面、上面、左面 ;
15、1375元 ;
16、5/2 ;
17、< ;
18、75O或15O
三、解答题
19、解:原式=
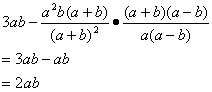
当![]()
原式=![]()
20、 (1) 不公平,因为小明获胜的概率为1/3,小于小刚获胜的概率2/3。(利用树状图说明) (2) 修改方案不唯一,符合要求即可.
21、解:(1)提示: 充分利用格点画图 ;
(2)A2(5,2);B1(-4,-5).
22、(1)获得圆珠笔的概率为: ![]() =
=![]()
(2)可采用“抓阄”或“抽签”等方法替代:
在一个不透明的箱子里放进360个除标号不同外,其他均一样的乒乓球,其中一个标“特”、10个标“1”、30个标“2”、90个标“3”、其余不标数字,摸出标有哪个奖次的乒乓球,则获相应等级的奖品。(本方案仅供参考)
23、解:(1)如果①②③,那么④⑤
证明:如图,延长AE交BC的延长线于F
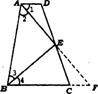 ∵AD∥BC ∴∠1=∠F
∵AD∥BC ∴∠1=∠F
又∵∠AED=∠CEF,DE=EC∴△ADE≌△FCE
∴AD=CF,AE=EF
∵∠l=∠F,∠1=∠2.∠2=∠F
∴AB=BF∴∠3=∠4
∴AD+BC=CF+BC=BF=AB
(说明:其它真命题的证明可参照上述过程相应给分)
(2)如果①②④,那么③⑤
如果①③④,那么②⑤
如果①③⑤,那么②④
(3)若(1)(2)中四个命题含假命题(“如果②③④,那么①⑤’’),则不加分;若(3)中含假命题,也不加分.
24、解:⑴设![]() ,它过点(60,5),(80,4)
,它过点(60,5),(80,4)
∴![]() 解得
解得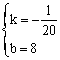
∴![]()
 ⑵
⑵![]()
∴当![]() 元时,最大年获得为60万元.
元时,最大年获得为60万元.
⑶令![]() ,得
,得![]() ,整理得:
,整理得: ![]()
解得:![]() ,
,![]()
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.
又因为销售单价越低,销售量越大,
所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
25、解:(1)连结AD,不难求得A(1,2![]() )
)
OE=![]() ,得E(0,
,得E(0,![]() )
)
(2)因为抛物线y=![]() 过点A、E
过点A、E
由待定系数法得:c=![]() ,b=
,b=![]()
抛物线的解析式为y=![]()
(3)大家记得这样一个常识吗?
“牵牛从点A出发,到河边l喝水,再到点B处吃草,走哪条路径最短?”即确定l上的点P
方法是作点A关于l的对称点A',连结A'B与l的交点P即为所求.
 |
本题中的AC就是“河”,B、D分别为“出发点”和“草地”。
由引例并证明后,得先作点D关于AC的对称点D',
连结BD'交AC于点P,则PB与PD的和取最小值,
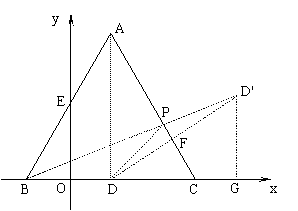 即△PBD的周长L取最小值。
即△PBD的周长L取最小值。
不难求得∠D'DC=30º
DF=![]() ,DD'=2
,DD'=2![]()
求得点D'的坐标为(4,![]() )
)
直线BD'的解析式为:![]() x+
x+![]()
直线AC的解析式为:![]()
求直线BD'与AC的交点可得点P的坐标(![]() ,
,![]() )。
)。
此时BD'=![]() =
=![]() =2
=2![]()
所以△PBD的最小周长L为2![]() +2
+2
把点P的坐标代入y=![]() 成立,所以此时点P在抛物线上。
成立,所以此时点P在抛物线上。
26、解:(1)由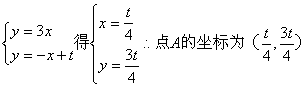 。
。
由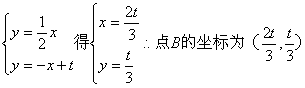
所以![]()
(2)由(1)知:点C的坐标为(![]() ),设直线OC的解析式为y=kx,根据题意得
),设直线OC的解析式为y=kx,根据题意得
![]()
![]()
(1) 由(1)(2)可知,正方形ABCD的边长
CB=![]()
(2) 设直线PD的解析式为y=k1x+b,由(1)知:
点D的坐标为 ![]() 代入得
代入得
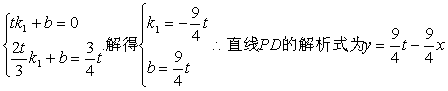
由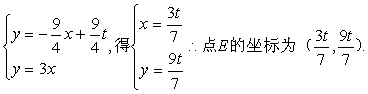
所以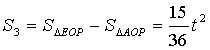
 三等奖
三等奖